Peg Solitaire is a puzzle game for one person, thought to be at least 300 years old and of French origin. It is part of the Sequential Movement class of mechanical puzzles. It is related to the game Fox and Geese. (Also see the entry for Fox and Geese at the University of Waterloo's Elliott Avedon Virtual Museum of Games.)

In his 1985 book The Ins & Outs of Peg Solitaire, John D. Beasley states that the origins of Solitaire are unknown, and that the earliest clear evidence of the game he found is this portrait of Anne Chabot de Rohan Princesse de Soubise, who lived 1648-1709, engraved by Claude-Auguste Berey in 1697 - the French Wikipedia article on Berey says he lived circa 1660-1730.

Another very similar engraving by Antoine Trouvain entitled Dame de Qualité Joüant au Solitaire (A Woman of Quality, Playing Solitaire), from Figures du règne de Louis XIV, vol 1, fol 105, dates from 1695 - two years earlier than the Berey engraving.

Beasley says he regards "the existence of Solitaire at the court of King Louis the XIV as adequately proven."

Beasley includes a quote from Gottfried Wilhelm Leibniz that appears in the 1710 Miscellanea Berolinensia I: "Not so very long ago there became widespread an excellent kind of game, called Solitaire, where I play on my own, but as if with a friend as witness and referee to see that I play correctly." (The Miscellanea Berolinensia (Berlin Miscellanea) was the primary journal of the Berlin Academy, and was published in seven volumes between 1710 and 1746.)

George Bell has done a lot of analysis of Peg Solitaire in its various forms. George's website offers all kinds of information and is definitely worth a visit! Also, at Alexander Bogomolny's Cut-the-Knot, there is a good explanation of the solution technique involving packages and purges, taken from Winning Ways for Your Mathematical Plays by Berlekamp, Conway, and Guy. Other statistics can be found at Jean-Charles Meyrignac's website euler.free.fr.

In their 2005 paper New Problems on Old Solitaire Boards (PDF), George Bell and John Beasley state that "The game appears ... to have been the 'Rubik's Cube' of the court of Louis XIV."

The game is played on a board having an arrangement of holes, with counters of some sort - typically pegs or marbles. The objective is to start with pegs in specific holes, and one or more vacant holes, then by legal jumping movements, remove pegs to achieve a goal configuration. A game where one must start with a full board save one empty hole, and end with one peg, is called a "single vacancy to single survivor" problem. When the initial empty hole and the location of the final peg must be the same, it is called the "complement problem."

Typically, a legal move is to jump a peg over an adjacent peg, in a straight line, either horizontally or vertically in any direction but not diagonally. Depending on the variant being played, sometimes diagonal jumps are permitted, or jumps in certain directions are prohibited. In addition, the game can be played in reverse (as noted by Leibniz) - start with a single peg and then by "reverse jumps" re-populate the board, with the objective of filling a specific field of holes.

The shape of the board and the arrangement of holes varies as well. Solitaire is usually played on a 33-hole cross-shaped board known as the "English" board (though according to Beasley this board type probably appeared in Germany before appearing in England). A standard notation labeling the holes on the English board assigned the letters abcdefg to the columns and the digits 1-7 to the rows. The center hole is thus d4. The standard problem on the English board is to start with all holes filled save the central hole, and end with a lone peg there - this is called the Central Game, or the d4 complement problem. Modern readers may be more familiar with the side-5 triangular variant offering diversion at tables in Cracker Barrel and other restaurants.

The portrait shows the Princess with the 37-hole French board, but on this board it is impossible to start with the central hole vacant and end with the last peg there. Bell and Beasley explain, "The unsolvability of the problem 'start by vacating the central hole, play to leave a single man in this hole' on the 37-hole board is a consequence of a property known as 'position class': the various positions possible on a Solitaire board can be divided into 16 different classes, and it is impossible to play from a position in one class to a position in another." It is usually assumed that diagonal moves are prohibited, but it really isn't known definitvely whether or not diagonal moves were allowed when this was devised, and if they are, then the central game on the 37-hole French board is solvable in 13 moves.

Example Solitaire Board Types
(from the Wikipedia article)

1. European (or Continental) board,  17th century, 37 holes 2. J. C. Wiegleb, Germany 1779, 45 holes 3. Asymmetrical 3-3-2-2, 20th century	4. The English Board, 33 holes 5. Diamond, 41 holes 6. Triangular (side-5), 15 holes
Click here to open a window and run my Triangle Solitaire Solver.

A puzzler improves at Solitaire by at first achieving the objective of leaving but a single peg in the correct hole (rather than two or more pegs isolated across the board, or even one peg but in the wrong hole), and then by reducing the number of moves required for the task to its minimum. The number of jumps will always be equal to or less than the number of initial pegs minus one, since every jump eliminates one peg - but the number of moves can be less if we count the same peg jumping more than one other peg in succession to be a single move. For a given configuration, an interesting mathematical and computational challenge is to determine this minimum, and the correct sequence of moves - indeed, to determine if a solution exists at all for a given starting configuration and objective. The shortest solution to the central game on the English board requires 18 moves, shown by Ernest Bergholt in 1912 and proved in 1964.

Many versions of Peg Solitaire have been produced. One particularly well-known version called Hi-Q was offered by Kohner in the 1950s and 60s. According to this article by Richard Gottlieb, the Kohner brothers Frank, Paul, and Michael played a major role in shaping the modern toy industry. Frank Kohner died on Feb. 6 2011 at the age of 100.

Cafe Puzzle - 1978 Gordon Bros. This is a vintage plastic peg solitaire set.

In the 1960's, Setko (aka the Set Screw and Mfg. Co. of Bartlett IL) offered a number of nice peg solitaire-type jumping and transposition puzzles. Some were "made for" Baekgaard & Butler - Glenview Ill. Several of them were designed by a Calvin O. Brown. Hoyle, Crestline, and even Skor-Mor offered similar sets.	Various box lid graphics, including a screw, crest, and alt. crest.
101 Cross The classic - set up pegs in all holes except center. Jump in straight line horizontally or vertically, not diagonally, & remove jumped peg. End in center hole.	102 Tri-Puzzler Walnut board, Oak board Another classic, but on a side-6 grid rather than the side-5 at Cracker Barrel. Start with one hole anywhere, jump & remove, end in a corner.
103 Reversal (Reverse All) 9 pegs of one color, 9 of another. Set up as shown. Jump forward (diagonally) or sideways, no removal. Reverse the setup vis colors.	104 3 Square eq. to Crestline's Cross Over and Skor-Mor's Switch Put 9 pegs of one color in lower right square & 9 pegs of the other color in upper left square. Jump up/down/left/right (not diagonally) over any color, without removal. Exchange the complete colored squares of 9.	105 Double Diamond The included instructions are unclear on the setup, and suggest the setup shown here, but the patent and the Hoyle version clarify - the setup should resemble the Hoyle picture I show. The 3 special pegs go in the circled holes. Jump, no removal, to move all pegs to the opposite diamond, with the special pegs in the corresponding circled holes. The instructions aren't clear on whether diagonal jumps are allowed. U.S. Patent 2778640 - Calvin O. Brown 1957
Hoyle Double Diamond	106 Bullseye Start with center, circled hole empty. Jump in any straight line, remove jumped peg, leave last peg in center.
Setko Bullseye II Start with center, circled hole empty. Jump & remove, any direction (including diagonally), end in circled hole.	107 Kan Yu Set up a side-6 triangle, with a special peg in the center of the row of 3 (a circled hole). Jump forward only - not backwards or sideways, no removal. Transfer all pegs to the opposite triangle, with the special peg in the corresponding circled hole. U.S. Patent 2712938 - Calvin O. Brown 1955	108 Zig Zag 8 pegs of one color, 7 of another. To begin, lay all the pegs in the groove, in some order you pick. Starting on the right end, move the first peg in line to the left end of the groove then place the next peg on the right into the first hole on the left of the top row of holes. Repeat, moving the first in line to the end and placing the next into the next available hole from left to right, top then second row of holes. The goal is to end with an alternating arrangement of colored pegs in the holes. You're trying to discover the starting lineup in the groove that will permit the goal to be reached when following the prescribed process. U.S. Patent 2778639 - Calvin O. Brown 1957 (The instructions actually give the wrong patent number - 2778640, which is for Double Diamond! The above is correct.)
Setko Fore and Aft Hoyle Fore and Aft 8 pegs of one color and 8 of another - set up as shown. When oriented as shown in the Setko photo, the dark pegs can move right or down only, the light pegs move left or up only. Jump over a peg of the opposite color, no removal. Reverse the starting setup vis colors. See U.S. Patent 522250 - Emerson 1894.		Hoyle Why No instructions with my copy. Eq. to Setko Puzzler 67
Setko 1971 Puzzler Fill all holes with pegs, remove one to start. Jump in any direction, removing jumped pegs. End in circled hole (left empty in photo).	Setko Red Puzzler No instructions included, but should be same as 1971.	Setko X (? - no name on package or board) No instructions included, but should be same as 1971.
Crestline Square Peg (eq. to Skor-Mor's Lonely Peg) Start as shown, jump & remove, end in center. Instructions aren't clear on whether diagonal jumps are allowed - I assume not.	Setko Mill Mill is a two-player game. The board starts empty.	Setko also packaged puzzles in sets - 3-Square, Mill, and Cross were included in a set; Tri, Reversal, Double Diamond, and Bullseye were offered in another set.
Mike Desilets is a fellow puzzle collector - he specializes in the Setko line and is working on a book about the history of the puzzles. We've never found an instance of this particular design by Calvin O. Brown, so we refer to it as the "Lost Setko." U.S. Patent 2778641 2778641 - Calvin O. Brown 1957. Mike made an example and kindly sent me a copy. Thanks, Mike! Start with the silver peg in either of the two circled holes. Place two black pegs to either side of the silver peg. Now, using only jumps of one peg over one other peg into a vacant spot, with no removal, get the silver peg to the other circled spot, again with two black pegs on either side. I discovered a sequence that moves the whole "train" one spot along - so the solution entails repeating this sequence until the whole train arrives in the proper positions - it's lengthy!
This Setko puzzle is a form of Latin Square, rather than a jumping puzzle - but I show it here since Setko made it. Setko Scramble Arrange the pegs so that no row, column, or main diagonal contains a duplicate letter, and so that "SETKO" is not spelled in any line.

This is the "Ancient Star Problem Puzzle." It is copyright 1949 Barters, Inc. and was issued by the Reflex Products Company of Cleveland. 36 numbered holes are arranged in a star pattern on the metal board, with radial lines, chords, and concentric circles printed to show allowable jumping paths. Various initial peg setups are given in the accompanying instructions sheet, and the challenge is to jump pegs until a single peg is left in the center hole. An insert challenged puzzlers of 1950 to send in unique problems for cash awards. See U.S. Patent 2569637 - Loe 1951 (assigned to Barters).

Here is another peg solitaire type puzzle with holes arranged in a star shape. (I don't have this - shown for reference.) This one was issued to advertise "Chas. H. Rickert's Cash Shoe Store" of Reading PA. See U.S. Patent 484882 awarded in Oct. 1892 to Charles Rickert. Center-complement goal. Evidently Rickert designed and patented his own puzzle to use as advertising for his shoe business.

This boxed set of four solitaire-type puzzles and logic games was issued by Skor-Mor. Included are: the Twenty To One Ball Puzzle (jump balls until only one remains in center), the 12 High Game (2 players move according to dice rolls), Six Man Morris, and the Nim-Wit Game.

Rather than jumping and removal, peg puzzles can have placement as their objective. On the left is the Eight Point Puzzle from Sherms. Use eight coins - place one on any of the eight points, then move the coin along one of the two lines from that point, to the opposite point and leave it there. Continue with another coin, placing it on one of the remaining vacant points and moving it as described, until seven of the eight points have been covered. You win if you can place seven coins as described, and can simply place the eighth coin on the last point. Galileo's Wheel was issued by Milton Bradley in 1962. It is similar in principle to the 8-Point puzzle, but with 10 points rather than 8. The blue base has 10 symmetrically spaced holes around its perimeter. There are 10 orange cones and a transparent hub piece that, when set on an existing cone position, indicates the two possible positions for the next cone - in lieu of the lines printed on the 8-Point card. The hub also serves as a storage cradle for the cones as shown. In "Star Craze," you choose a hole in which to place the first peg. Each subsequent placement may be made only in a hole connected to the previously placed peg by lines on the board. The objective is to fill all the holes.

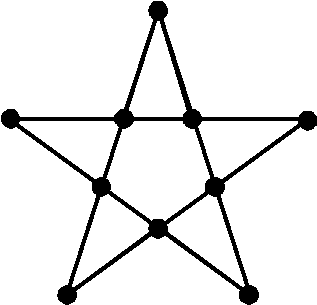
Pentalpha Played on a pentagonal star shaped board, using the ten points and line intersections - highlighted by circles in the diagram. Play with 9 coins or other markers. A move consists of starting on an empty circle, moving in a straight line over one empty or occupied circle, landing on a third circle which must be empty, and placing a marker there. Continue until no more moves are possible - the goal is to end with all nine markers placed and a single remaining empty circle. A pentagram is among several diagrams incised into stone slabs comprising the roof of the Temple of Kurna at Thebes, dating to the rule of Rameses I circa 1400 B.C. The diagrams are supposedly gaming boards, cut there by the stonemasons who were shaping the slabs in the quarries. Three of the various diagrams were partly cut away when the stones were finally trimmed and placed in the roof of the temple.

Peg puzzles can also have transposition as their objective. A peg can either move forward, or jump a peg in front of it (but neither is removed). The object is to exchange the two sets of pegs. See U.S. Patent 243688 - Bullard 1881. The left-hand version of peg solitaire is similar to "Teez" offered by Tryne. I have also heard it called "Mountain Goats" - pretend the pegs are two lines of mountain goats traveling in opposite directions on a narrow mountain path, who need to pass but the path is only wide enough for one goat so they must jump over each other. Also pictured is Hop Over by Pressman. Kohner's Switch poses several transposition challenges. On the right is a vintage British metal puzzle called Draught Board - identical in principle to Hop Over.

I found a second Draught Board puzzle - but this second one (the gold-hued one in the comparison photos) is an inferior copy of the original silver-hued version I have. In particular, see the photos of the backs of the two puzzles. The copy is blank, while the original has instructions and a registry number (594918).

Martin Gardner mentions in his book The Last Recreations that the minimum number of moves necessary to exchange the two sides of checkers pieces without forcing any jumps has been proven to be 120. Anthony Filipiak in his book 100 Puzzles - How to Make and Solve Them discusses several peg problems, including some played in linear fashion, on a circular board, and on a Chinese Checkers board. Filipiak describes a simple and interesting variation using just 3 bicolor pegs, that can be played just as well with 3 coins. Align the 3 coins with the 2 end coins heads-up and the center coin tails-up. Now, in exactly three moves, where a move consists of flipping any two coins in place, get all 3 coins either heads up or tails up. (Re-read the previous sentence if you're thinking, "I can solve that in one move!" You need to do it in "exactly three moves.") A vintage Presidential Muddle Puzzle - see U.S. Patent 524703 - Carter Aug. 1894. It is sturdy metal and larger than I thought. I like it a lot. I had found a copy that is missing a button.

Balance the Wheel, No. 108 "An L. J. Gordon creation" by Peterson Games of Sacramento CA, 1972. The box claims it is "A puzzle which becomes increasingly difficult as you get closer and closer to the ultimate objective." A transposition puzzle akin to Hop Over, around a circular track, with six pegs of each of two colors.

The "Lucky Plucky Lindy Bird Puzzle" (I don't have this - shown for reference.) Copyright 1927 by W. N. Ebling Eight wooden pieces each with one letter from "LINDBERG" - I believe there are 10 numbered spaces. Start with the pieces at: E1 D2 G3 I4 R5 L6 B7 N8. Move two adjacent blocks at a time into any two vacant adjacent spaces. In four such moves, rearrange the letters to spell LINDBERG. Then, starting with the letters where they end up, make the same type of move, end with GREBDNIL, using any number of moves.

Mariner's Mate - a peg solitaire variant from Venture Puzzles & Games 1989

Azig - a vintage sequential movement puzzle, from Japan. I had wanted to find one of these since I saw it on Jaap's Puzzle Page years ago, and finally have!

Other examples of puzzles where moves are governed by rules rather than physically:

Rubik's Triamid	Switchback - Binary Arts	Think and Jump - Pressman	Thinkfun's Stormy Seas
This is Binary Arts' Lunar Lockout. You can read about the genesis of this puzzle and a computer analysis of it on John Rausch's site. You can play Lunar Lockout on-line here.	Pete's Pike - Thinkfun An updated version of Lunar Lockout.	TipOver - Thinkfun	Hoppers - Binary Arts
Leapin' Lizards - Binary Arts	Hot Spot - Thinkfun	Subtrax - Thinkfun	Cool Moves (a type of peg solitaire) by Discovery Toys
Oops! - from Foxmind 50 challenges - set up the pieces as indicated by the challenge card. Goal is to end with a stack having the hat on the bottom and the head on the top. The hat cannot move. A stack can move orthogonally a number of spaces equal to the number of pieces contained in the stack. Every move must end on top of another piece, culminating of course with the hat.		Solitaire Chess invented by Vesa Timonen For each of 60 challenges of graduated difficulty, successively capture pieces using legal chess moves until only one remains.

This puzzle is called Right On and was produced by Skor Mor. There are five colored pegs each of which can hold seven discs. There are twenty discs, four of each peg color. The instructions give an initial arrangement of the discs. The goal is to get all four discs of each color onto their corresponding pegs. You can only transfer one or a stack of two adjacent discs at a time, and the bottom moving disc must land either on an empty peg of its color, or on another disc of its color. It can be done in 26 moves.

Right On appears identical to this 1984 puzzle I do not have, from Marks and Spencer, called "Stack It."

The Olympic WanderRings seem to be a version of the same puzzle. They were produced by Logical Toys in Hungary as a souvenir of the 100th Olympic Games, held in Atlanta.

This puzzle asks you to achieve a specific goal ordering of objects given an initial ordering and constraints on moving the objects.

The set of objects are the nine ("traditional") planets and the initial ordering from left to right is:

[Earth Venus Pluto Jupiter Mars Uranus Neptune Saturn Mercury]

The goal ordering is the “natural” ordering:

[Pluto Neptune Uranus Saturn Jupiter Mars Earth Venus Mercury]

The rules for movements are as follows:

• A move adjusts the ordering of the sequence.
• Exactly 4 moves - no more and no less - must be made to adjust the order from that of the initial state into the goal state. After the fourth move, the ordering must be the goal ordering.
• A move consists of taking 3 adjacent planets from anywhere in the sequence, and preserving the ordering of the subset of 3, extracting them from the sequence and prepending them to the left end of the sequence, leaving the remaining planets in order (closing the gap created).

For example, a legal first move would be to take the subset (Venus Pluto Jupiter) and move it to the left, resulting in the new state: [Venus Pluto Jupiter Earth Mars Uranus Neptune Saturn Mercury]

The Exhaustive Method

One approach to a solution is an exhaustive search of all possible moves. This entails exploring all the possible legal moves (many of which will not be smart moves) while not missing any, and ideally also not unnecessarily repeating any. The search can be organized as a tree, with the initial state as the root, each node representing a particular ordering/state, and each edge representing a specific legal move. The limit of four moves defines the exact depth at which all branches must terminate. On termination, each leaf node will be either a solution equal to the goal ordering or a non-solution indicating an unsuccessful sequence of four moves. The search may terminate when the first leaf node equal to the goal state is found, unless an enumeration of all possible solutions is required in which case the entire tree must be realized.

The size of this tree can be determined as follows. From the initial state, there are 6 possible moves - you can choose any group of 3 adjacent planets beginning with the second from the left (Venus) and ending with the third from the right (Neptune). In fact, at each level of the tree, from each node, there will always be 6 possible moves. In four moves, there will be 6*6*6*6 = 1296 possible branches. While the exploration of this tree can be automated, doing it by hand will be tedious and time-consuming (unless by luck a solution branch is found early). However, the problem can be approached heuristically using some puzzle-solving techniques I’ll explain below.

Working Backwards

First, one should look at the goal state and work backwards to see if additional constraints can be deduced which can serve to reduce the search space. This technique is sometimes fruitful when solving mazes, for example, especially mazes constructed by hand since often the psychology of the maze-maker leads them to unconsciously build in more choices near the entrance and fewer near the exit.

In the case of the Aligning the Planets puzzle, we have the following. Examining the goal state we can deduce with certainty that the last (4th) move must put the leftmost 3 planets into their proper positions. This means that the 4th move must take the subset (Pluto Neptune Uranus) from somewhere in the sequence and move it to the left end intact. Furthermore, at that point the rest of the sequence must also be in its final goal form. This means that prior to this 4th move, Saturn must be on the left end.

What must be to the immediate right of Saturn at this time (i.e. prior to the 4th move but after the 3rd move)? There are only two possibilities: either the (Pluto Neptune Uranus) subset must itself have come from there, or the required Jupiter must already be there, since only the 4th move remains so there would be no other way to get Jupiter to where it is needed.

Let’s find a helpful way to diagram what we’ve deduced so far:

Initial state: [Earth Venus Pluto Jupiter Mars Uranus Neptune Saturn Mercury]

Possible States after 1st move: (6 of them)…
Possible States after 2nd move: (36 of them)…
Viable States after 3rd move:

• Saturn Jupiter …
• Saturn (Pluto Neptune Uranus) Jupiter Mars Earth Venus Mercury

Goal state after 4th move: [Pluto Neptune Uranus Saturn Jupiter Mars Earth Venus Mercury]

Viable means that the state can lead to the required next state - in this case the goal state - in one move.

Simplifying the Problem

To make further progress, we employ the mathematical technique of making an assumption, then showing that either the assumption leads to a contradiction or absurdity, in which case it must be false, or that we can prove the assumption true.

The assumption I’ll investigate is as follows. Note that in the initial state, Earth Venus and Mercury, though not yet adjacent, are already in the correct order. Is it possible that the only planets that must be moved are the middle six (Pluto Jupiter Mars Uranus Neptune Saturn)? Note that moving them would ensure that they end up to the left of Earth and Venus, and we leave Mercury where it is, eventually resulting in Earth Venus Mercury in order on the right as required.

If we look at only these middle six planets, we have effectively reduced the search space - we have simplified the problem to finding a way to order just these six planets correctly. The size of the search tree is more tractable since now within these six planets there are only three possible moves at any time.

Bear in mind that if our assumption is false - i.e. that the true solution in fact requires moves that involve any of Earth Venus Mercury, then we will have to explore the entire tree for the six planets and show there are no solutions within it to this reduced problem. However, this smaller tree for the six planets has 3*3*3*3 = only 81 branches.

We can employ the same strategy of looking backwards from the goal on this subset as we did on the whole set. By working simultaneously forward from the initial state and backwards from the goal we might be able to see a solution more easily.

Our diagram now looks like the following.

Initial state: [Pluto Jupiter Mars Uranus Neptune Saturn]

All Possible States after 1st move:

• Pluto (Jupiter Mars Uranus) Neptune Saturn --> a) Jupiter Mars Uranus Pluto Neptune Saturn
• Pluto Jupiter (Mars Uranus Neptune) Saturn --> b) Mars Uranus Neptune Pluto Jupiter Saturn
• Pluto Jupiter Mars (Uranus Neptune Saturn) --> c) Uranus Neptune Saturn Pluto Jupiter Mars

Possible States after 2nd move: ?

Viable States after 3rd move:

• x) Saturn Jupiter Mars (Pluto Neptune Uranus)
• y) Saturn Jupiter (Pluto Neptune Uranus) Mars
• z) Saturn (Pluto Neptune Uranus) Jupiter Mars

Goal state after 4th move: [Pluto Neptune Uranus Saturn Jupiter Mars]

Bridging the Gap - An Intuitive Leap

Now our problem is to find a (or show there is no) second move and resulting state that bridges the gap from one of the 3 possible states a-c shown after the 1st move, to one of the 3 viable states x-z shown after the 3rd move.

A methodical exploration begins with an examination of the 3 possible 2nd moves and resulting states available from (a):

• a) Jupiter (Mars Uranus Pluto) Neptune Saturn --> 1: Mars Uranus Pluto Jupiter Neptune Saturn
• a) Jupiter Mars (Uranus Pluto Neptune) Saturn --> 2: Uranus Pluto Neptune Jupiter Mars Saturn
• a) Jupiter Mars Uranus (Pluto Neptune Saturn) --> 3: Pluto Neptune Saturn Jupiter Mars Uranus

Are any of these states 1-3 one legal move away from any of the 3 viable states x-z?

By inspection, we can find that, yes, in fact #3 is. From #3, we can make the move (Saturn Jupiter Mars) to end up with (x) the first viable alternative: Saturn Jupiter Mars Pluto Neptune Uranus.

We have found our bridge and validated our assumption. In fact, if we now piece together our conclusions, we have solved the puzzle by finding a sequence of four moves that accomplishes the goal.

Granted, it was fortunate that we only had to examine part of even the reduced six-planet tree before running across a solution. If the puzzle had been constructed so that our assumption was false, we would have had more work to do to prove that. In fact, puzzle makers do this to increase the difficulty and/or “elegance” of their puzzles - deliberately craft the puzzle conditions and constraints so that a solution does not arise by chance easily.

A Solution

The solution we’ve found is as follows. The subset of planets to be moved is enclosed in parenthesis in each state, beginning with the initial state. Per our assumption, Earth Venus and Mercury are never moved. The last state is the goal.

• Earth Venus Pluto (Jupiter Mars Uranus) Neptune Saturn Mercury -- move (a)
• Jupiter Mars Uranus Earth Venus (Pluto Neptune Saturn) Mercury -- move (3)
• Pluto Neptune (Saturn Jupiter Mars) Uranus Earth Venus Mercury -- bridge move to (x)
• Saturn Jupiter Mars (Pluto Neptune Uranus) Earth Venus Mercury -- state (x) and required last move
• Pluto Neptune Uranus Saturn Jupiter Mars Earth Venus Mercury