

 Edge-Matching puzzles usually consist of a set of tiles whose edges have various distinct patterns, symbols,
or colors.
The objective is to arrange the tiles in a grid such that abutting edges "match" according to some rule.
Since the tiles can be printed on cardboard, these puzzles can be inexpensive to produce
and in the past have served extensively as advertising promotions and giveaways.
There are many modern edgematching puzzles - you may have heard of "Scramble Squares" for example.
Jacques Haubrich published his definitive Compendium of Card Matching Puzzles in three volumes,
in which he describes over 1000 puzzles,
and a companion
volume called About, Beyond, and Behind Card Matching Puzzles in which he provides interesting
theoretical and historical analyses.
According to Haubrich, and to Slocum and Botermans in their 1986 book Puzzles Old and New,
the first edge-matching puzzle patent was applied for in 1880
by Edwin Lajette Thurston of Cleveland, Ohio (b.1857 in MA, d.1921)
and granted in 1892 - see
487797 and
487798; also see 1893's
490689.
Thurston was, of all things, a patent attorney!
For a precursor to the edge-matching puzzle, using triangular tiles like "Triominoes,"
see U.S. Patent
331652 - Richards 1885.
Richards doesn't claim the triangular form of the dominoes, but rather the ways to make and mark them.
He never uses the word "puzzle" - he describes a number of games but none come close to being a puzzle.
Edge-Matching puzzles usually consist of a set of tiles whose edges have various distinct patterns, symbols,
or colors.
The objective is to arrange the tiles in a grid such that abutting edges "match" according to some rule.
Since the tiles can be printed on cardboard, these puzzles can be inexpensive to produce
and in the past have served extensively as advertising promotions and giveaways.
There are many modern edgematching puzzles - you may have heard of "Scramble Squares" for example.
Jacques Haubrich published his definitive Compendium of Card Matching Puzzles in three volumes,
in which he describes over 1000 puzzles,
and a companion
volume called About, Beyond, and Behind Card Matching Puzzles in which he provides interesting
theoretical and historical analyses.
According to Haubrich, and to Slocum and Botermans in their 1986 book Puzzles Old and New,
the first edge-matching puzzle patent was applied for in 1880
by Edwin Lajette Thurston of Cleveland, Ohio (b.1857 in MA, d.1921)
and granted in 1892 - see
487797 and
487798; also see 1893's
490689.
Thurston was, of all things, a patent attorney!
For a precursor to the edge-matching puzzle, using triangular tiles like "Triominoes,"
see U.S. Patent
331652 - Richards 1885.
Richards doesn't claim the triangular form of the dominoes, but rather the ways to make and mark them.
He never uses the word "puzzle" - he describes a number of games but none come close to being a puzzle.
 In Hoffmann's 1893 Puzzles Old and New, the only edge-matching type puzzles mentioned are #72 in chapter IV
"The Royal Aquarium Thirteen Puzzle" (equivalent to the French Le Nombre Treize),
and #18 in chapter III "The Endless Chain" (equivalent to the French La Chaine sans Fin).
Major Percy Alexander MacMahon and his friend Major Julian R. Jocelyn applied for a patent in Great Britian in 1892
(#3297 - I could not find a copy online - it is reproduced in Haubrich's About,...)
in which they describe several triangular tile games and puzzles.
In his 1921 book New Mathematical Pastimes, MacMahon published some of the first material to treat edgematching
puzzles with mathematical rigor.
That work also discusses his 3-D puzzle Colored Cubes, first introduced in a lecture he gave in 1893.
Tile-laying puzzles (in German, "Legespiel") of both the edge-matching and polyform varieties have been explored and
produced by Kate Jones at Kadon,
and you can read a lot of interesting material at the Kadon site -
see Edgematching Colors and Shapes, and
More About Edgematching.
You can see
Erich Freidmann's collection here.
You can see some original designs by
Yukio Hirose here.
Take a look at George Hart's article
"A Color-Matching Dissection of the Rhombic
Enneacontahedron."
Also see
Peter Esser's page.
And Toby Gottfried's site.
In Hoffmann's 1893 Puzzles Old and New, the only edge-matching type puzzles mentioned are #72 in chapter IV
"The Royal Aquarium Thirteen Puzzle" (equivalent to the French Le Nombre Treize),
and #18 in chapter III "The Endless Chain" (equivalent to the French La Chaine sans Fin).
Major Percy Alexander MacMahon and his friend Major Julian R. Jocelyn applied for a patent in Great Britian in 1892
(#3297 - I could not find a copy online - it is reproduced in Haubrich's About,...)
in which they describe several triangular tile games and puzzles.
In his 1921 book New Mathematical Pastimes, MacMahon published some of the first material to treat edgematching
puzzles with mathematical rigor.
That work also discusses his 3-D puzzle Colored Cubes, first introduced in a lecture he gave in 1893.
Tile-laying puzzles (in German, "Legespiel") of both the edge-matching and polyform varieties have been explored and
produced by Kate Jones at Kadon,
and you can read a lot of interesting material at the Kadon site -
see Edgematching Colors and Shapes, and
More About Edgematching.
You can see
Erich Freidmann's collection here.
You can see some original designs by
Yukio Hirose here.
Take a look at George Hart's article
"A Color-Matching Dissection of the Rhombic
Enneacontahedron."
Also see
Peter Esser's page.
And Toby Gottfried's site.
Jacques suggests the following seven categories:
|
|
|
Jacques also defines a classification scheme by which one can identify the puzzles abstractly and find isomorphisms (i.e. equivalent puzzles).
Jacques' conclusions, based on computer analysis, regarding the best approach to solving these puzzles agree with my empirical findings - in general, fix the tile in the middle and work around it. A good tile to choose for this middle position is the tile with the most possible matches.
As discussed in my polyforms section, the only regular polygons which can be used to completely tile the plane are the equilateral triangle, the square, and the hexagon. It is evident in Haubrich's Compendium that these shapes comprise the majority of tile shapes used in existing edgematching puzzles. Rectangles have also been used, as have octagons (allowing empty areas). I've organized my example puzzles by tile shape:| [Square Tiles] | [Hexagonal Tiles] | [Triangular Tiles] | [Other Tiles] |
Some puzzles have tiled surfaces other than a plane - e.g. the platonic solids, or a cylinder. I would file such things under 3-D edgematching puzzles.

The Thurston design was used by Calumet ca. 1930 as advertising for their products. In the Calumet Puzzle, one must match not just the proper color edges, but also the corresponding top and bottom halves of the baking powder cans. I solved the Calumet puzzle using a variant of my Drive Ya Nuts technique. |



The Grandpa's Wonder Soap Puzzle was patented (U.S. Patent 1006878) in 1911 by A.K. Rankin. It is described on page 36 of Slocum and Botermans' "Puzzles Old & New." The goal is to form a 3x3 grid such that at the points where the quarter-circles on the corners of the tiles meet (either four or two), there are always different colors on each of the meeting quarter-circles. Grandpa's head must always be upright on every card, so the cards cannot be rotated. Jacques says this is the first example of a corner dismatching puzzle. There are different versions. |

The Besco Soap Puzzle - from the Beaver Soap Company of Dayton Ohio. Form a 3x3 grid such that there are four different colors in each circle at the corners, and two different colors in each half-circle. There must also be a different color at each of the four corners of the grid. The pieces must all remain oriented with the words "Besco Soap" upright. JH Vol.2 p163- 2 solns |

Le Berger Malin - The Lazy Shepherd (N.K. Atlas Paris circa 1910). NOTE: "malin" can also be translated as "ingenious." There are nine tiles, each of which is divided into four quadrants by two diagonals. There is a number in each quadrant, and the corresponding number of sheep are depicted. Arrange the tiles in a 3x3 grid such that the total in each square formed where edges meet totals 10. According to Jacques, this is the first known example of a Heads/Tails puzzle (the two numbers which must add to ten comprising the head and tail). |

Le Fermier Avise - The Wise Farmer The same principle as the Lazy Shepherd, except with chickens and now it's a wise farmer. |

This is a French puzzle (Casse-Tete) called "Le Nombre Treize" - The Number Thirteen. Arrange the tiles in a 3x3 square such that the red figures align vertically and the blue figures align horizontally, and such that the three figures in each of the six rows and six columns add to 13. |

The Vess Cola Nine Piece Puzzle is an advertising giveaway, promoting Vess Cola; its pieces are equivalent to the Calumet Puzzle. |


The Vess Mystery Puzzle two versions |

Here is a 3x3 heads/tails that Norman Sandfield found on a visit to the remote Easter Island (Rapa Nui). He bought all he could find, and I got one from him at the 2006 New York Puzzle Party. |



Vess Billion Bubble Beverages Mystery Puzzle - a vintage 9-card advertising edgematching puzzle |
||



Cleo Cola Nine-Piece Puzzle A vintage advertising edge-matching puzzle. |
||

Pepsi edgematching puzzle (Spanish) |

La Canadienne - an advertising promotion edgematching puzzle |
|


The "33 to 1" Puzzle, advertising Pabst beer. Copyright 1940. One version shows bottles, the other cans. |

Pabst 33 - arrange the cards in a 3x3 grid so that the numbers total 33 horizontally, vertically, and along the main diagonals. |

Pel-Freez Puzzle JH Vol.1 p93 - two solns |



A-Treat Mystery Puzzle - A-Treat Bottling Co. PA Three versions. |
Jacques' Compendium, Volume 1, pp72-4, indicates that the following 9-square puzzles are isomorphic and have only one solution:
|


Nestle Nine-Square |

Lionstone Whisky, Kentucky 1973 |

Camel - an advertising promo from a cigarette manufacturer. |

Bits and Pieces - match the color dots on the squares' edges |

Nitty Gritty - Arrange the colored tiles in the tray so that the edge patterns on all adjacent tiles match. |

In Mattel's Mangle Quadrangle one also has to arrange the colored tiles in the tray so that the edge patterns on all adjacent tiles match. One in a series of Brain Drain puzzles. |




Loncraine Broxton/Lagoon Games offers a set of four Professor McBrainy's Zany optical illusion puzzles: Fusion, Cosmos, Vortex, and Kaleidoscope. The patterns are psychedelic. |
|
Ovals - Nob - O-Pico/Color Match Puzzland Hikimi JH Vol.1 p151 - 6 solns |

Chelona Pocket Puzzle - Cats A nine-square edge matching puzzle from Chelona in Greece. Cute, colorful graphics on thin plywood. Novel packaging - an extra backing tile has an attached elastic cord to enclose the stacked tiles. A solution diagram is on the bottom. Available from Padilly. |

Crafty Butterfly |


IZZI - Binary Arts Geo Matrix made by Binary Arts for The Museum Company is the same. (I don't have Geomatrix.) JH Vol.2 p303 |


Zoki See U.S. Patent 5524898 - Pavlovic 1996 |


At the January 2007 Toy Fair, Tomy launched the Eternity II puzzle (Wikipedia entry here) and a contest prize of $2M USD. Eternity II employs 256 square tiles to be arranged in a 16x16 grid, which must have a gray border and a particular tile at a given "starting" position. The "final scrutiny date" passed without a winner, so the prize went unclaimed. |


Scramble Squares Tropical Fish Sea Shells There are many different versions of Scramble Squares, and most of them are in fact distinct puzzles (not just the same puzzle with different pictures). |

12 Ladies, from the Dr. Wood Mind Challenge series. |

A Tens Edgematching puzzle from the Plantecs at PuzzleMePlease.com. Same idea as Le Berger Malin. |

One Tough Puzzle is a 3x3 heads/tails edge-matching puzzle. I solved it using an extension of the technique I describe for the Drive Ya Nuts. JH Vol.1 p107 |

Another Tough Puzzle is a 7-piece hexagonal heads/tails edge-matching puzzle. (I have listed it here with the original One Tough Puzzle.) JH Vol.1 p35 - 1 soln |

Another Tough Puzzle (Triangles) - Great American Puzzle Factory |


The Ultimate Puzzle (4x4 square tiles)
The Ultimate Puzzle Two (3x3 right triangle tiles) Both designed by Lee Willcott of Estonia. The original version has square tiles - each side has a cutout or tab, in one of four shapes: an "in" arrow, an "out" arrow, a cross, or an oval. There are four challenges: build a 2x2; build a 3x3 (find 9 tiles that work); build a 4x4 with no side-up constraint; build a 4x4 with either all smooth sides or all rough sides up. The Ultimate Puzzle Two has 18 right-triangular tiles, pairs of which form squares. Nine squares must be arranged in a 3x3 grid (so I have listed it here in the square tiles section with the original version). Each tile has a cutout on each side - the cutouts form halves of four symbols: crown, heart, spade, and star. On one pair of tiles, a heart on the diagonal is offset - the bumps half is lower and the v half is deeper. Where tiles touch the halves must form a whole symbol, so this is a "heads and tails" type edgematching puzzle. |
||

DaMert 3D Squares Cars |

4D Metapuzzle |

4D Metapuzzle No. 4 |

Instant Insanity - Hexagon Puzzles 1986 JH Vol.1 p151 - 2 solns |

A four-piece glass edge-matching puzzle made by Brett. |

The Great Canadian Puzzle |

Setko Match Heads |


Peterson Uptight Spider JH Vol.1 p149 - 1316 solns |

The Wobbly Web Create a rectangle from the 15 square tiles such that web strands join (edgematching). JH Vol.2 p210 (See the Waddington's series, below.) |

Peek-a-Boo Snakes |

Eye-Cue |

Pin Pin Kan |

New Departure Puzzle - advertising New Departure coaster brakes for bicycles. An uncut card. Copyright 1953. |

Celtic Knotwork |

Lagoon Group Safari series - Tiger Puzzle |

Warning - Lagoon |

Jungle Mega Puzzle - Lagoon |

Vintage Chevrolet advertising edgematch. |


"Ladybugs," a "3D Magna Puzzle" by Caeco, purchased from New England Hobby. 16 magnetic square tiles. A holographic image that is 3D when viewed from two orientations, and flat from two others. This is more of a jigsaw since each edge really has only one mate. |

A British Petroleum (BP) advertising edgematching puzzle from Australia. |

The Crazy Cheese Puzzle, from Blue Orange Games. A nice wooden 3x3 edge-matching puzzle with two levels of challenge. Purchased at The Games People Play. |
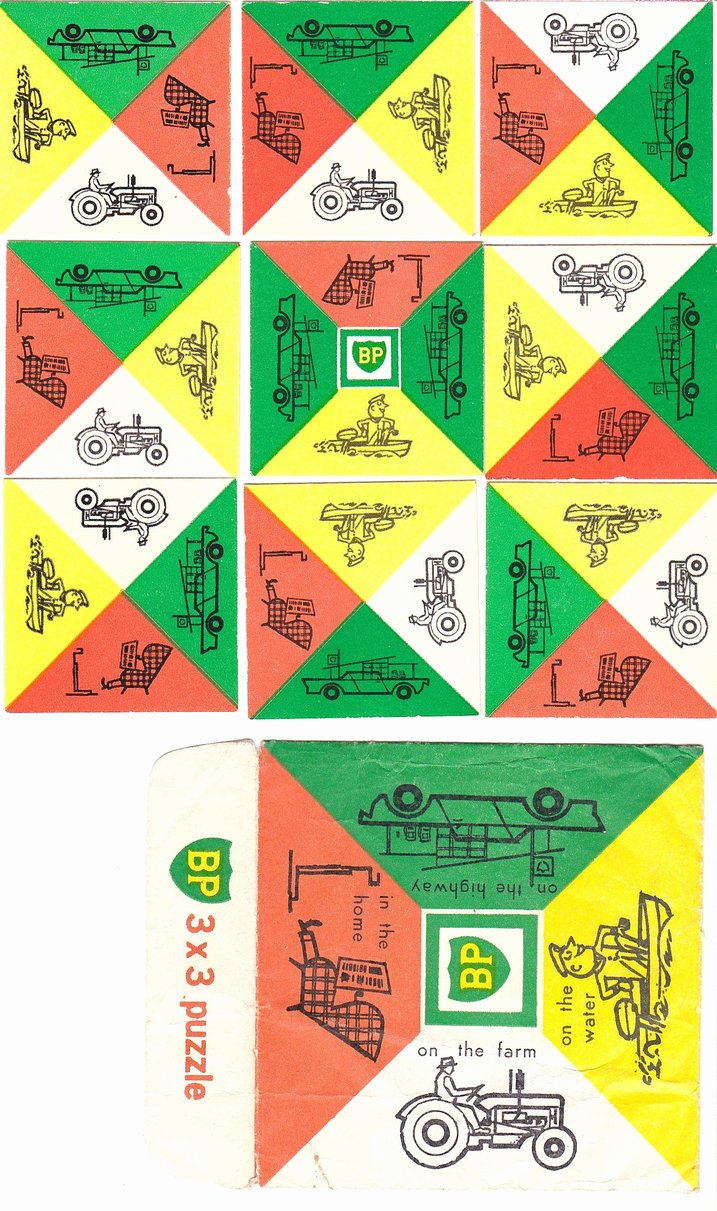

I found a second example of this nice, colorful, vintage edgematching puzzle advertising BP, and made a better image. |
||

Holland America Edgematching puzzle |

Suits Edgematch I found this at Der Verrückte Laden, a puzzle shop in Berlin. |

Perfect 10 from Creative Crafthouse |
A vintage advertising cardboard edgematching challenge, the Snyder Standard Nine Piece Puzzle.
According to the package, "Par is tweleve minutes."


|
||

Norton Abrasives - a vintage 9-piece edgematching advertising puzzle. |
||

 This vintage six-piece, square-tile edgematching puzzle from Germany is called the Matador Dominoes-Puzzle.
This vintage six-piece, square-tile edgematching puzzle from Germany is called the Matador Dominoes-Puzzle.
The backs of the tiles are blank. I have solved it, so it can be done. |
||



Fish Frenzy - arrange the eight cards to form a picture, then move the cards about to form other pictures. |
||


Colour Rings Puzzle-friend Colin James kindly sent me a copy of this nine-square edgematching (or dis-matching) puzzle. Thanks, Colin! |

Quadrant 9 - a 9 square edgematching puzzle by Dan Gilbert, issued by DaMert 1995 Each piece is two-sided. A gift from author Joe Konrath - Thanks! |

Three Pipe Problem - a 9 square edgematching puzzle by Peter Schaefer, issued by International Polygonics 1983 |



The Nine A laser-cut acrylic 3x3 edgematching challenge. From The CraftySmiths (Jeff and Kate Smith) |
||

The Daily Mail World Record Net Sale puzzle was published in 1920 and has only one solution. See British Patent No. 173588 - Hydes and Whitehouse 1921. It was printed and published for Associated Newspapers, Ltd. by the Chad Valley Co. Ltd of Harborne, England. It consists of 19 hexagonal tiles which must be arranged in a large hexagonal grid 3 tiles on a side, while matching the color and the word on adjacent tile sides. The newspaper ran a contest and offered various prizes, and my copy came with a yellowed newspaper clipping showing the winner - one Mr. C. Lewis of Dalston - and the solution. JH Vol.2 p246 |


The Nestle's puzzle, published around 1930-1940, was the first 7-tile hexagonal edgematching puzzle. I found one from Malaysia, and one printed in Spanish. There have been many variants, including the modern "Drive Ya Nuts." JH Vol.1 p30 - 1 soln |
|


To me, the edge-matching puzzle is exemplified by the more recent but none-the-less venerable Drive Ya Nuts. I developed a tabular solution, shown below. There was also a version with red nuts in a silver case - it has the same numbering. |

The Circus Seven by Masudaya is fairly well-known. In principle it is the same as Drive Ya Nuts, but with tents and colors instead of nuts and numbers. I solved mine easily using my tabular technique. |

The Circus Puzzler is a clone - many variations exist. |

7 Nut Puzzler - by Shackman I believe this wooden version predates the Milton Bradley plastic version of "Drive Ya Nuts" (copyright 1987) but this has the same set of nut configurations and the same solution. |
||

Dunlop Hexagons |

Lyons' Tea |

Match the Colors - Adams ca. 1953 |

Gemstone - Nordevco |


Pressman's Think-Ominos |

Melissa & Doug make a similar puzzle called the "Space Edge Matching" brain-teaser |

Spider Puzzle - Toysmith |

Hexamania From The Long Point Toy Co. of Ingersoll, Ontario. 19 single-sided hexagonal tiles numbered 1 through 19, each having the edges differently numbered 2 through 7. Arrange the pieces in an edge-3 hexagonal grid (i.e. 5 rows - 3/4/5/4/3) such that all adjacent edges total 9. A heads/tails type of edgematching puzzle. |

Another Tough Puzzle is a 7-piece hexagonal heads/tails edge-matching puzzle. (I have also listed it with the original One Tough Puzzle.) JH Vol.1 p35 - 1 soln |

Pair It - made by Steve Kelsey Arrange the seven hexagonal pieces such that edges match. |
||

The OXO Triangle puzzle. This was published in 1922 by the OXO Company for a contest. There are 25 equilateral-triangular cards/tiles, numbered 1 through 25. The tiles must be arranged into a side-5 large triangle such that at each point where the corners of different tiles meet, the colors are different, and such that at each point where three tiles meet they spell "OXO" and where six tiles meet they spell "OXOXOX." There are 104,920 solutions but finding even one by hand is very difficult. JH Vol.2 p271 |

Tri-Puzzle - Lagoon |

Contack A game (not really a puzzle), played with 36 triangular pieces. The 3 sides of each triangle are different in colour, and each side has a number from 1 to 10 printed at its edge. Players try, by matching color and number, or matching color and making certain score totals, to play all the triangles from their hand and to make as large a score as possible. Listed at Boardgamegeek. |

Butterflies Mini |

Travel Triazzle |

12 Triangles - Majak |


Playtime Flower Puzzle General Toys No. 210 Hong Kong |

BrainArt Level 4 - Ekos Designed by Klaus Schröer Arrange the 24 equilateral triangular tiles into a hexagon with one lizard in each cube, then solve four riddles. |

BrainArt Infinity - Ekos Designed by Klaus Schröer Arrange the 24 equilateral triangular tiles into a hexagon so that only one continuous snake is formed, then solve a hidden mystery. |


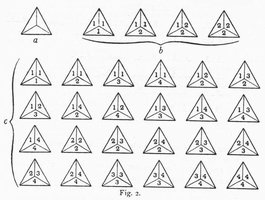

Jinxed, a vintage edgematching puzzle by Tryne. There are 24 triangular tiles, the edges of which are colored with a dot in one of four colors (red, yellow, white, and green). The tiles are to be arranged into a hexagon such that all touching edges match and the border is all red. (It is possible to solve the puzzle with other border constraints, too.) Puzzles using triangular tiles are discussed by MacMahon in New Mathematical Pastimes on pages 2-22. MacMahon shows the possible tile sets for 1, 2, and 4 colors in Figure 2, and gives a solution for the 4-color set. Kadon's Multimatch III is essentially the same puzzle. |
||



Coloured Triangles Puzzles - British Caledonian Airways Magnetic pieces. Similar to Jinxed a vintage edgematching puzzle from Tryne. Puzzles using triangular tiles are discussed by MacMahon in New Mathematical Pastimes on pages 2-22. |
||

Another Tough Puzzle (Triangles) - Great American Puzzle Factory (Also listed with the original One Tough Puzzle that has square tiles.) |

Triazzle - Alice in Wonderland |
|

This is L'Arc en Ciel (The Arc in the Sky - i.e. the Rainbow). There are nine discs on pegs, arranged in a 3x3 grid of holes in a baseboard. Each disc has four diamonds arranged pointing north, south, east, and west. Each diamond is one of eight colors: red, green, yellow, orange, gray, white, pink, and blue. The discs must be arranged such that no color appears more than once in each of the three rows and three columns of six diamonds. In this case, not every color appears in every row or column. There is a second constraint - when a pair of colors is placed adjacent horizontally, then that same pair cannot be placed adjacent again in that direction - likewise for the vertical. JH Vol.1 p162 - 236,326 solns |



Tile-O-Rama Called the "Wonder Mosaic Puzzle" when it first appeared circa 1925, this was the first design with rectangular tiles. (I have a loose copy but it was also included in the F.A.O. Schwartz Deluxe Puzzle Chest No. 3006.) I also have the Mosaik and Tesa Mosaic Square puzzles discussed in Slocum and Botermans' "The Book of Ingenious & Diabolical Puzzles" on p.23. |

Here is a new favorite, an RGB Roundup from Elverson. The basic puzzle is to build a circle in the provided tray, such that adjoining colored dots match. Additional objectives include building various shapes like in Tangrams. The pieces are made of very nice weight plastic material like Mah-Jong tiles. |

Vintage Set of Four Colorful Circular Torture Puzzles by Shackman |


IZZI 2 - Binary Arts Color Matrix made by Binary Arts for The Museum Company is the same. JH Vol.2 p198 |

Domino Match |

Double Half - Interkemia 1981 |

Block Shock |

Ed Pegg, Jr. developed the game Chaos Tiles based on a non-periodic tiling. I've read that Ed has yet to determine if the shapes can in fact completely tile the plane. |





A set of four Jungle Bungle edgematching puzzles designed by Dan Gilbert. Issued by DaMert in 1992. Each has eight pieces - form a square such that pictures on abutting edges match. Large pieces on nice heavy cardstock. Hummingbirds, Flowers, Butterflies, and Beetles. |
||

Around the Barn |

Concentra Atlantis Dan Gilbert 1994 A circular edgematching puzzle with pentagonal pieces. Not too difficult since the die cuts give clues. |

Try Nine - Copyright 1981 Reiss Games Arrange the nine octagons in a 3x3 grid such that abutting edges match. You must simultaneously match edges diagonally across the small void squares! |

Smiley - designed by Kunio Saeki and Frederic Boucher - Frederic's exchange at IPP35. A 3x3 edgematching puzzle. Each piece is basically a 45mm square where each side has one of four types of triangular notches or corresponding tabs. Each piece has a smiley face on only one side, so the pieces cannot be flipped, though they may be rotated. Any piece may be placed in the center. |
||
|
In this group of puzzles, several rods have been cut into fragments of different lengths -
these must be fit into a base containing sockets drilled to different depths, such that the completed stacks all achieve the same height. |
||

In Kohner's Even Steven, match pegs to sleeves such that all pegs align at the same height. U.S. Patent 3375009 - Stubbmann 1968 |

Here is another version of Even Steven, with blue plastic rod pieces to be inserted into a clear base. |
|

In Reiss' Flat Top, arrange the eight pegs in the four holes so that each stack ends up at the same height. |

Tekozuru Z2 from Hikimi - purchased from Torito |

Adele and Peter Plantec at Puzzle Me Please sent me a selection of their beautiful puzzles crafted from exotic woods. This one is called Double Dowel. Thanks! |
|
These three puzzles, Nice Cubes, Mental Blocks, and Double Disaster, each comprise a set of
transparent cubes with colored markings.
Their goals, respectively, are: to line up four cubes so all four long sides each show all four colors;
to create a cube so that embedded colored rods match where the pieces touch; and
to create a cube such that each side shows all four colors, then such that each side shows a solid color.
Double Disaster was offered by Scientific Games Division of KMS Industries Inc. of Ann Arbor Michigan, and its
insert mentions the other two. Mental Blocks was offered by Creative Playthings.
The Nice Cubes in their original package say Copyright 1968 Funtastic, Div. of KMS Industries, Inc., Alexandria, VA. 



|
||

This is Aquarium designed by Kohfuh Satoh. I bought it at Torito.
Three challenges - no incomplete fish ever allowed to show, but unless otherwise noted fish may span edges/turn corners:
1. Use 3 pieces and build a 1x2x3 showing 7 fish. 2. Use all 4 pieces and build a 2x2x2 showing 9 fish. It is also possible to show only 8 or 7. 3. Use all 4 pieces and build a 2x2x2 showing only 6 fish with none turning any corner. |

The Dodeca Nona puzzle comprises a dodecahedral magnetic body, and 12 2-sided pentagonal tiles. The tiles are numbered 1-5 at their vertices in all possible orderings. The objective is to arrange the tiles around the dodecahedron so that the 3 numbers that meet at each vertex add up to nine. JH Vol.2 p202 |

Integr8, from the Dr. Wood Mind Challenge series. Arrange the 8 cubes into a larger cube such that only complete circles show on the sides - no semicircles or lines can be visible. |
Here is a solution for Integr8:


|
||




This puzzle, called Crux, was made (in Hong Kong) back in 1972 by the Hubley Division of Gabriel Industries - it's marked "Copyright 1972 Gabriel Ind. Inc." It is a version of the Piet Hein design Triple Cross (that I do not own). It consists of six plastic pieces, each with four color spots on the sides. Twist the blocks to ensure that at each intersection, there are three different (or same) colored spots. Pieces are paired by elastic cords threaded through the narrow end and anchored inside on hooks molded on the back plates. The elastic cords had long since worn out, but you can easily pop out the back plate by poking an unbent paper clip through the hole. I replaced the cords with rubber bands. If any of the internal plastic hooks are broken, just anchor the band with a paper clip. |
||



Mental Misery (aka Double Trouble) - Lakeside A transparent box, a frame which fits inside the box and will hold four cards vertically against the box sides, and five cards each colored with four colors front and back. The four colors are red, yellow, green, and blue. Arrange the cards on five sides of the cube so that edges match inside and outside the cube. The instructions are marked: Made in Hong Kong, Lakeside Industries, a division of Liesure Dynamics, Inc. Minneapolis Minnesota. Copyright 1970 Leisure Dynamics, Inc. The box is marked: Copyright 1969 L.I.I. Made in Hong Kong. The frame is marked: Copyright 1969 Lakeside Toy Division of Lakeside Industries Inc. Made in Hong Kong. |

The Great Pyramid Pocket Puzzle, by Eliot Inventions Wales 1981, is a tetrahedron with 4 equilateral triangular tiles pegged to each side. The triangles are printed on one side only with a series of radiating wedges of different widths. The objective is to arrange the triangles so the edge patterns on all adjacent triangles match. The larger version with 9 triangles per side carried a 25,000 GBP prize for the first solver. I have no idea if it was ever awarded. The small case is a mini-puzzle in itself - a 2-piece trick box. |
|

Another oldie but goodie is On-the-level by Mag Nif. Fit 9 multi-level pieces into a 3x3 grid such that wherever 2 pieces meet along an edge it is at the same level. In addition, the solution must be "toroidal" - i.e. opposite outside edges must all also match. JH Vol.1 p161 |

In Contoura, arrange the blocks so that the surface contour is correct. |

Four Cube Impossible Puzzle - Binary Arts 1998 Created by Scott Nelson in 1971 - maps the 24 3-color MacMahon squares to the faces of four cubes such that all edges match. The puzzle gives 13 arrangements to make and requires that all adjoining edges match. Analyzed by Jaap. |

Chain of Colors - Haubrich IPP26 |

Ey-Ko-Se Imperial Games Ltd. Southport England Edgematching triangular tiles on the faces of an icosahedron. Alternative challenges include total 15 on every pentagon of five triangular faces, or show a 5-letter word on every pentagon. |

Einstein Cube |

Dodek-Duo Issued by the Dodek Puzzle Company (dead link?) Designed by Jerry Langin-Hooper 12 magnetic pentagonal pyramid pieces form a dodecahedron. The edges of each pentagonal face have a color (one of five), and a small black shape (one of rectangle, semicircle, triangle). Try to assemble the dodecahedron such that the colors match at face edges (only one solution), then such that the small shapes match (47 solutions, but much more difficult to find). It isn't possible to do both simultaneously. Analyzed by Jaap. |

Dodecahedral edgematching - R.D. Rose Purchased from Norman Sandfield at IPP 29 in SF. |
|



The Enigma (a dodecahedral edge-matching puzzle) by Reiss, 1971 |
||

Colin James sent me a rare Twitchit puzzle, issued in 1972 by the Hubley Division of Gabriel Industries of Lancaster PA, and designed by Piet Hein. This is a dodecahedron whose faces turn. One of three symbols (a circle, square, or triangle) is printed at every vertex of every pentagonal face. The objective of the puzzle is to rotate the faces (in place) so that at all 20 vertices of the dodecahedron, three different symbols show. Although discolored with age, the plastic remains intact and the puzzle is playable. I solved it! Thanks very much, Colin! |



I obtained a copy of the Hubley Toys 1972 Catalog, which features a series of four puzzles designed by Piet Hein. With the acquisition of the Twitchit, I now have an example of each of these vintage Piet Hein puzzles. |
|


Hungarian Rock - a vintage 3D edgematching twisty puzzle |
||

Tetra Twist - designed by Marcel Gillen - issued by Brainwright. Tetra Twist comprises four two-layer, four-sided tiles. The layers of a tile rotate relative to each other. Each side posesses a protruding shape - a triangle, semicircle, half-square, or half-hexagon, or a correspondingly-shaped indent. There are several challenges where you must abut corresponding shapes at both levels of tiles simultaneously, including the task of making a 2x2 arrangement where all four bi-layer matings are correct, which has a unique solution. A handy enclosure is included. I really like this one! Thanks, Alison! |


Star Brush Cube - a vintage wooden advertising pattern puzzle |
|
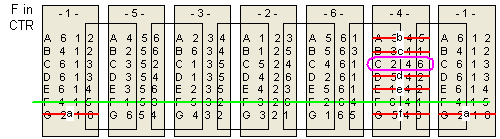
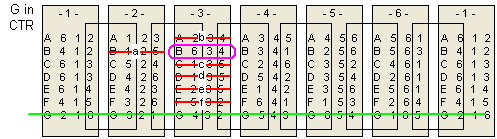
 The following is my graphical (or tabular) solution to the Drive Ya Nuts puzzle.
I have not seen any solution technique like mine applied to this type of puzzle -
even
Jaap's page
says one must try all combinations. My technique is a considerable savings and allows
a solution - and negative results - to be derived easily by inspection - the hallmark of a graphical technique.
I have worked this entirely "by hand."
Using this technique I can prove fairly easily that this puzzle has only one distinct solution.
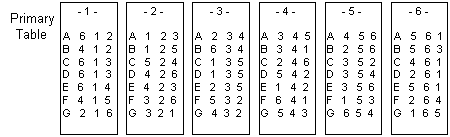
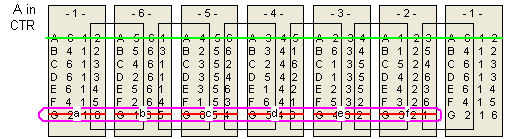
There are seven hexagonal "nuts" that I label A thru G.
For each nut, the six sides are numbered 1 through 6 in some order.
The numbering scheme of each nut, starting with 1 and proceeding CLOCKWISE,
along with the letter ID I arbitrarily assign the nut, is shown below:
The following is my graphical (or tabular) solution to the Drive Ya Nuts puzzle.
I have not seen any solution technique like mine applied to this type of puzzle -
even
Jaap's page
says one must try all combinations. My technique is a considerable savings and allows
a solution - and negative results - to be derived easily by inspection - the hallmark of a graphical technique.
I have worked this entirely "by hand."
Using this technique I can prove fairly easily that this puzzle has only one distinct solution.
There are seven hexagonal "nuts" that I label A thru G.
For each nut, the six sides are numbered 1 through 6 in some order.
The numbering scheme of each nut, starting with 1 and proceeding CLOCKWISE,
along with the letter ID I arbitrarily assign the nut, is shown below:
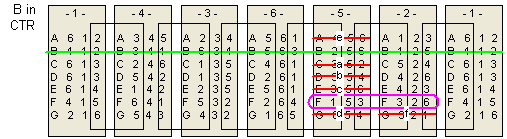
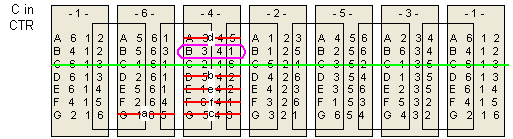
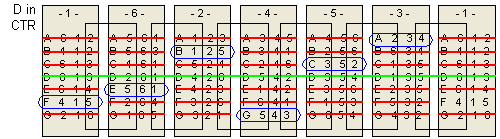
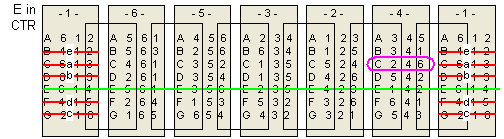
Route Building puzzles are a sub-class of Edge Matching puzzles ("Continuous Path" or CP Edge Matching puzzles according to Jacques Haubrich's classification scheme). Here, one has to arrange pieces so that connections are made, creating a specific route across the pieces according to some rule.


La Chaine Sans Fin - The Endless Chain A vintage version, and a recent laser-cut wooden version by Steve Kelsey. Arrange the pieces in the tray to form a closed loop of chain links. JH Vol.2 p244 |

Tantrix is a well-known modern route-building puzzle/game. [Jaap's Tantrix page.] |

Psyche-Paths (c) 1969 Funtastic, Division of KMS Industries, Inc., Alexandria, VA. A set of 85 hexagonal tiles, each with 3 path segments using up to 3 colors. A solitaire challenge is to build a 9x10 rectangle alternating rows of 9 and 8 tiles. Listed at boardgamegeek.com. Tiles shown here. Play a related game, Kaliko, online here. Here is the included solution to another solitaire challenge: 
|
|


Rubik's Tangle set of #1 thru #4, and the 9 double-sided plastic tiles version The original sets have 25 one-sided cardboard tiles, and come in four versions distinguished by which particular tile is duplicated within the set. JH Vol.2 pp272-3 |
|||

Chicago L - George Miller |

I believe this is the "IQ Chain" puzzle, by D.P.B. Taiwan 1993 JH Vol.2 p172 - 1 soln for a single continuous path. |

Krazee Links - Plastrix 1939 JH Vol.2 p207 |


The Path - from Family Games |

It's Knot Easy - Milton Bradley JH Vol.2 p240 |

Trail Run |


Think Through - Pressman (Equivalent to QED's Set Squares which I don't have.) |

Right Connections - Springbok JH Vol.2 p179 |

Fishy - Melissa & Doug |

Snake Pit - Nature's Spaces / Binary Arts |

Octopus - Nature's Spaces / Binary Arts JH Vol.2 p184 |
|


Go-Getter 3 Prince and Dragon, and Cat and Mouse - DaMert Designed by Raf Peeters - see his website at www.atelier-oker.com |

|

The Path - Waddington's JH Vol.2 p197 (See the Waddington's series, below.) |

Ant Trails |



The Diamond Dilemma puzzle was Copyright by Price Stern Sloan Limited in 1989, and offered prizes for solutions of various complexity. The instructions tell you to "arrange the playing pieces on the diamond so that a continuous unbroken line is formed." |

This is Dice Dominoes. The box says "Made in U.K." but there's no other provenance. There are twelve cubes, each side of which shows a correctly linked arrangement of two or three dominoes. Paraphrasing from the instructions: Using the box base as the playing area, start with a double-six in the top left corner. (There are six faces among four of the cubes showing a double-six.) The box holds a rectangle of 3x4 cubes. Match dice so a continuous pattern is formed, as in regular dominoes. You must use all 28 dominoes and cannot use any domino more than once. Each must line up and doubles must be at right angles. A solution sheet (I haven't looked) is enclosed. |
||


TSL Maze Assemble the pieces to form a maze. |

Daily Sketch Jig-Saw Puzzle Fit the pieces into the tray and build a loop. |

Serpentiles - Thinkfun |

Metroville from Smart Games, designed by Raf Peeters - see his website at www.atelier-oker.com |

HooDoo Loop by Popular Playthings Build a path using the 14 pieces. Designed by Bill Hanlon and Steve Wagner A gift from the folks at Oy Sloyd Ab. Thanks! |

Cobra Cubes, from SmartZone Games. Designed by Ariel Laden. Purchased at Eureka. Four cubes, each a different color. Each cube's sides have various segments of a snake - a head, tail, or body section. A booklet of challenges, graded A, B, C, or D, requires one to arrange the cubes in order to form a snake that spans all visible faces of the required cubes. |

Anaconda - designed by Raf Peeters A 5x5 grid with one corner filled, seven 2-sided pieces, and a 1x1 blank piece. Cover a designated square with the blank, then fill in the rest with the other pieces while building a complete snake. |

Tromino Trails from Pavel Curtis IPP31 Berlin Using subsets of Tromino pieces inscribed with trail segments, make a single closed loop in five different-sized openings in the adjustable tray. |

String Octet Designed by Goh Pit Khiam, made by Walter Hoppe. Purchased from Walter at IPP 29 in SF. 8 1x2 tiles encompassing all the ways a tab and a notch can be arranged, each with a path inscribed connecting the tab and notch. Two 1x1 tiles, one with a notch and one with a tab - the start and end tiles respectively. A 4x5 tray. A sheet with 13 challenges - each specifies positions and orientations for the start and end tiles. The objective is to connect the 1x2 tiles in the tray to create an unbroken path from start to end. I really like this one! |


World Passport, from SmartZone Games. Designed by Tzafrir Kazula. Purchased at Eureka. Fit six poly-hex pieces into a hexagonal grid overlaid on a "country" card such that five points are connected in order by a transparent path, with no backtracking. |
||


Troy Extra Muros from Smart Games, designed by Raf Peeters. I really like this one! A series of challenge cards indicate the placement of up to 4 blue and 4 red soldiers. Place the four wall pieces such that all blue soldiers are completely enclosed and all red soldiers are "outside" the walls ("Extra Muros"). (You are finding the route the walls must take.) Raf gave an interesting talk at IPP31 in Berlin, in which he said that one goal of design is to ensure a customer can apprehend the goal of a puzzle just by looking at it in the package. He achieved that in this case - I could tell what the goal was despite the fact that I found this in Québec City and this box was printed in French! |

Golf Line by Binary Arts 1994 Arrange 20 1x1x2 rectangular cards depicting sections of an 18-hole golf course to form a continuous cart path from hole to hole. Hints and solution are included. |
||
Mall Function, designed and exchanged at IPP32 by Rik van Grol, made by Buttonius |

Network Builder, designed, made, and exchanged at IPP32 by Wei-Hwa Huang |


Temple Trap - designed by Raf Peeters, issued by Smart Games A 3x3 board with an exit space in one corner. Eight sliding blocks representing walls, hallways, and stairs in various configurations, and a player figure. Set up the blocks and figure per the current challenge, then try to solve it by sliding the blocks and moving the figure from block to block to eventually exit the board. The block where the figure resides cannot be moved, and the figure can only be moved to rest on certain blocks. Temple Trap combines a sliding-piece puzzle with route-building challenges and has a great theme reminiscent of Indiana Jones. |
|

Perplexing Python issued by Pentangle |
|||


Roundabout - invented by Volker Latussek Produced by Popular Playthings Use the 18 pieces of four different shapes to build a closed loop - assemble 50 challenges. |

City Maze - designed by Raf Peeters, produced by SmartGames Thanks, Raf! |
||


Puzzle Picks, by Kohner (No. 122) 1967. Includes a set of colorful plastic "matchsticks," a booklet of 80 puzzles, and a solution sheet. |
There are lots of matchstick puzzles on-line...
The book Creative Puzzles of the World by van Delft and Botermans includes a section on matchstick puzzles on pages 49 through 56. |

A set of brightly colored matchsticks, in a matchbox marked "Puzzle" from Japan. |


Allumez les Enigmes, produced by Kikigagne. A set of matches and cards posing 50 matchstick challenges (in French). Thanks, Brett! |
||


33 Problems - issued by Invicta in 1981 A board containing a set of grooves, arranged so as to provide a playing surface on which to try 33 different matchstick puzzles using a bunch of included red panels in lieu of matchsticks. The panels fit into grooves in the board. An included sheet specifies the setup and objective for 33 puzzles, but does not give solutions. |
||

The Case of the Smoking Pipe - Professor Puzzle The Smoking Pipe contains a set of matchstick puzzles and a pipe - remove the ash from the pipe without touching either. |
||
This category requires you to arrange the pieces to satisfy some rule or goal relating to a pattern/silhouette the pieces make. There is no physical mechanism to restrict moves - only rules or the goal govern legal combinations. The piece shapes will be fairly abstract but usually it will be easy to abut them and they will interchange positions easily.
Note: I have created a separate page for Tangrams.

This classic three-piece French puzzle is called Bucephale. Arrange the three pieces to form a horse. Described in Slocum and Botermans' New Book of Puzzles on page 23. Sam Loyd called it his Pony Puzzle. |

Demon Dino - William Waite |

Dino Try - William Waite |

Six Australian Animals designed by René Dawir |




Cliko, by Foxmind Comes with a set of blocks and a booklet of problems. Arrange specific blocks to form different silhouettes. With the Tangramino, Equilibrio, and Architecto books from Foxmind, I can use the pieces in the Cliko set I already have, to try many new challenges. |
|||

Blockistry - from blockistry.com - use the four identical pieces to produce each of the silhouette challenges. Some proved surprisingly difficult - you have to properly account for simplified perspective. |
|||

Copy Device - Hiroshi Yamamoto Place the 3 pieces flat in the tray to create two identical green areas. Winner of a Jury Honorable Mention in the IPP34 Nob Yoshigahara Puzzle Design Competition. |
|||
In this category of puzzle, a set of pieces, often transparent or with cutouts, must be stacked (or folded) over one another in order to achieve some goal.

The Rabbit Silhouette or "Question du Lapin" Layer the five cutouts to form a rabbit Play the rabbit silhouette on-line. |


Arrange the 5 layers so the cumulative cutout area forms the shape of a pipe. You will then have "This is Not A Pipe" - "Ceci n'est pas une pipe" - as from Rene Magritte's "The Treason of Images." A miniature puzzle in a matchbox. |

Mattel's Virtual Illusion puzzle contains a base and a series of transparencies each containing a portion of a three-dimensional image. You need to order the transparencies in the base so that the image appears correctly. |


Two Silhouette Puzzles designed by Diniar Namdarian- make a Pigeon, and make a Dog. |
||







Red All Through |

Animal Land |
Starry Skies |
Transposer 6

|
Bonbons
|
Genesis
|
|
Kaboozle |
Tiffany
|
Tower of London
|
Struzzle |

Along the same lines as the Toyo Glass puzzles, combined with the weave concept, Strip Tease requires you to create a 5x5 weave using 10 clear strips having various arrangements of quarter-squares so that all solid squares result. |

Trixxy designed by Dror Green - superpose four cards having transparent and opaque colored sections in order to produce a solid column of each of the four colors. |

This is the "2D 3D Burr" - stack the transparencies so that the image of a 3-piece burr appears. I bought it at Torito. |

Cover Your Tracks - Thinkfun Four pieces and a set of challenge cards - for each card, pack the four pieces into the tray so that the bootprints on the card are all covered. |

Zoo Panic by Tsugumitsu Noji Purchased at IPP28 in Prague. Four transparent overlays, each with a 6-unit enclosure. On each problem background, fence off unlike things. |

Frustables by Gameophiles Unlimited 1973 Six sets of six cards. Each set of six cards has one colored puzzle on the front and another color on the back - twelve puzzles in all. A card has a given color, and may have some black area. The objective given the six cards belonging to a given puzzle is to pile the cards such that all the black areas are covered but no colored area is covered. These are difficult puzzles! |



Ariel Laden's Kookoo Puzzles - Funny Fliers Four six-card puzzles, and one large puzzle using the backs of all 24 cards. Position and interleave the cards of a set to form a complete picture. This principle is very similar to that of the 1973 puzzle Frustables by Gameophiles Unlimited. |
||




Four well done puzzle challenges (and two expansion packs) from Smart Games.
Booster packs for North Pole Camouflage and Safari Hide & Seek |


Angry Birds Playground Under Construction - designed by Raf Peeters, issued by Smart Games Using the four pieces (non-flippable F, P, T, and U pentominoes), cover the proper selection of faces on the 5x5 gameboard, per each challenge. I admit I had trouble with the very first problem! |
|

Mozaniac: Four Painters By Paradoxy Products. Six square cards, each almost cut into quarters and each bearing a portion of four different images. Interlock and overlap the cards to create each image, in turn. |

The Invisible Puzzle, designed by Rich Garner, from Loncraine Broxton - Lagoon Trading Co. Ltd. Make a large hexagon from 18 transparent trapezoidal tiles, while matching edge colors. |

On the Dot - Gamewright |

Get a Clue from Pavel Curtis. A refined version of Pavel's exchange puzzle from IPP30. Nine transparent pieces, and a frame in the shape of a magnifying glass. Arrange the pieces in three layers inside the frame. Find two distinct overall arrangements to determine "two things given to Snow White." I enjoyed this one - it is not too difficult. |
||

Pathwords invented by Derrick Niederman For each of 40 challenges of graduated difficulty, fit a subset of the supplied transparent pieces to completely cover the field of letters such that each piece covers one word that runs backwards or forwards. |

Cage the Animal, designed by Manabu Satou and Naoyuki Iwase (Osho), made by Woodpecker Hikimi and Lixy, exchanged at IPP32 by Lixy Yamada |

Daily Puzzle - designed by Wei-Hwa Huang and Oskar van Deventer, produced by Thinkfun Six tiles must be paired and overlaid in variuous ways to form 3-latter month abbreviations, and four tiles must be similarly arranged to produce the date. Each tile has either black segments, cutout segments (through which whatever is behind the tile, including the black base) will show, or blank area. |

On the Line - issued by Brainwright A set of graduated overlay-pattern-assembly challenges. Arrange four identical transparencies to form a given shape. |

Star Shuffle 2 Stack the four disks so that a star appears in all twelve holes. From The Puzzle & Craft Factory |
|







This is a vintage Weave-O-Gram puzzle, copyright 1951 by Edcraft-Century. See US Patent 2439583 - awarded to Israel Shamah of London on Apr. 13, 1948.
From the patent description - the Weave-O-Gram "comprises a framework and a plurality" (patent lawyers love that term) "of flexible bands some extending in one direction and the others at right angles thereto, the various bands being interwoven... and each being capable of relative movement. On each band there is provided a number of sections of a picture... by relative adjustment of the individual bands the various sections of the picture may be juxtaposed so that a complete picture is formed. Each band will be provided with the sections of a number of different pictures so that a number of different complete pictures may be made up." My copy allows one to make six different circus scenes. The bands move pretty freely, occasionally catching on small rough edges or tears. It is best to use both hands to move a band, slowly, from both edges of the frame simultaneously. As you might expect, Weave-O-Gram is not too challenging, however the graphics are nice and this is a great implementation of one of those ideas that seems obvious once you've seen it done. Also see the earlier US Patent 1903226 awarded to Harry Lawson Perry of Jamaica, New York on Mar. 28 1933. Perry's device employs linear strips rather than looped bands. Then see the later US Patent 3235262 - awarded to Ernest Frankl of Middleboro, MA on Feb. 15, 1966. It is pretty much a copy of Shamah's idea - Frankl's improvements are to "effect economies of manufacture and assembly and to provide for ease of manipulation and attractiveness." Frankl assigned his patent to Winthrop-Atkins Co. Inc. of Middleboro MA, a printing company now owned by Chilcote Co. of Ohio. From the book Classic Century Powerboats by Frank, Trudi, and Paul Miklos copyright 2002, published by MBI Publishing Company of St. Paul MN. I learned that the company Century (as of March 2012 purchased by Allcraft Marine) makes powerboats, and was founded in Milwaukee in 1926. In 1948, F. L. "Ted" Hewitt Jr. became president. Since boat production orders were seasonal - heavy from March through July and slack during the rest of the year, one of Hewitt's initiatives was to offset the downtimes by producing other, stable products such as toys. Century produced a line of educational toys under the brand Edcraft, including Weave-O-Gram. Shamah also patented (in the UK) a locking mechanism for a money box.
|
||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||


The Frustr8tor From my friends at Puzzlemaster.ca - thanks, guys! 28 versions of the 8 Queens to solve. The front side shows an 8x8 grid. The back side has 8 tracks corresponding to the 8 columns of the grid. Along each track, each of the 8 row positions is marked by a number from 1 to 28 - some appear three times, some two. One red and one green tab ride in each track - green at the top and red below. To try a puzzle, choose a number and set a red tab at every position marked by that number. Then, using the green tabs in the remaining six columns, fill in the grid according to the usual rules - a dot appears in the grid on the front at the position where a tab is set. |


This vintage French boxed version called "Jeu des Manifestants" uses 8 tiles, and is available in two versions with either triangular or rectangular tiles. Jeu des Manifestants is shown in Slocum and Botermans' "Puzzles Old & New" on page 37. For another version using battleships, see U.S. Patent 1151615 - Reibstein 1915. |
|||||||||||||||||||||||||||||||||||||||||||

Lots O Spots by Peterson - "an L. J. Gordon creation." 16 tiles, each divided into four quadrants, and with 1 or 2 spots on each. When the tile are arranged in a 4x4 grid, the quadrants define 8 rows and 8 columns. The spots come in three colors - red, purple, and green - and are distributed so that there are 8 of each color. In the hardest of four challenges, you must arrange the tiles in a 4x4 grid such that all rows, columns, main diagonals, and all short diagonals contain no more than one spot of each color. This amounts to solving the 8 queens problem simultaneously for 3 colors of queens. |


The Schpotz puzzle by Peterson Games. Arrange the nine tiles in a 3x3 grid such that every row, column, and main diagonal contains exactly three spots. |

This is Out of Line by Crisloid Plastics of Providence RI. The objective is to arrange the eight pegs in the 8x8 grid so that no more than one peg is in any row, column, or diagonal. In addition, at least one peg must be in each of the five differently shaded areas - one of the areas is a single position at the lower right corner. The cover shows a motorcycle gang - I think they're supposed to be "out of line." |
||||||||||||||||||||||||||||||||||||||||||
|

 The first two challenges cited on the first instructions, on the 4x4 and 6x6 grids, are easy since you can use more than 4 and 6 colors respectively.
However, the 8x8 challenge amounts to superimposing 8 solutions of the 8 queens problem, and is impossible!
This puzzle is interesting because it requires superposition, and also because it seems to be one of those rare instances where prize money is offered for an impossible challenge.
The first two challenges cited on the first instructions, on the 4x4 and 6x6 grids, are easy since you can use more than 4 and 6 colors respectively.
However, the 8x8 challenge amounts to superimposing 8 solutions of the 8 queens problem, and is impossible!
This puzzle is interesting because it requires superposition, and also because it seems to be one of those rare instances where prize money is offered for an impossible challenge.
|
||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||

The Pin and Dot puzzle - "Insert six pins, each in a separate dot, so that no two pins shall be on the same line." This is equivalent to a six-queens puzzle. (I don't have this - shown for reference.) |
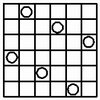
The six-queens puzzle has only one unique solution.
Since that solution is 180-degree symmetric, it has only four rotations and reflections.
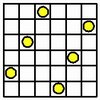
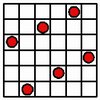
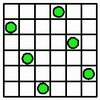
|





La Strategie des Nippons, Strategie des Boers, and Nouvelle Strategie These vintage French boxed puzzles are all instances of the six-queens puzzle. (I don't have these - shown for reference.) |
||||||||||||||||||||||||||||||||||||||||||


Jeu des Sentinelles "A police chief represented by the red piece, with 7 sentinels represented by the white pieces, must position himself and his sentinels so that no man can see any of the other men along any straight vertical, horizontal, or diagonal line." This vintage French boxed puzzle is an instance of the eight-queens puzzle. (I don't have this - shown for reference.) |

L'Intraitable - "The Intractable" Given a 6x6 grid and 24 tokens - six each of four colors, arrange the tokens on the grid so that no horizontal, vertical, or diagonal line contains more than one token of the same color. This vintage French boxed puzzle is an instance of a superposition of four six-queens puzzles. (I don't have this - shown for reference.) The four rotations and reflections of the six-queens solution can be superimposed: 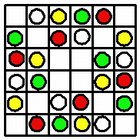
|



L'Embarras du Brigadier and L'Embarras du Caporal Given a 5x7 grid of points and 12 men, arrange the men on the grid to form six rows with four men in each row. Both of these vintage French boxed puzzles are instances of, using Singmaster's notation, a (12,6,4) configuration problem. (I don't have these - shown for reference.) Singmaster cites several appearances of the (12,6,4) problem, including in The Sociable of 1858 (as Problem 26, The Gardener's Puzzle), The Book of 500 Curious Puzzles of 1859, and Hoffmann (1893) Chapter VI, No. V.  There is a second solution (see
The Sociable, or Hoffmann), but it does not fit on the 5x7 grid.
Note that some (a,b,c) configuration solutions rely on the trick of stacking more than one token at a given point.
There is a second solution (see
The Sociable, or Hoffmann), but it does not fit on the 5x7 grid.
Note that some (a,b,c) configuration solutions rely on the trick of stacking more than one token at a given point.
|
||||||||||||||||||||||||||||||||||||||||||
The Five-Queens puzzle has only two unique solutions.
 The asymmetric solution has eight rotations and reflections.
The symmetric solution has only two, giving a total of 10.
A selection of five can be superimposed.
The asymmetric solution has eight rotations and reflections.
The symmetric solution has only two, giving a total of 10.
A selection of five can be superimposed.

|
The Seven-Queens puzzle has six unique solutions, and 40 rotations/reflections.
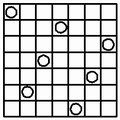
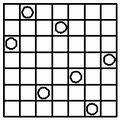
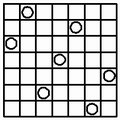
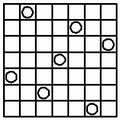
|
|||||||||||||||||||||||||||||||||||||||||||

The Elusive Spy - by Alexander Beresford, produced by Creative Crafthouse Includes eight 1x2 tiles wherein one must position the Spy tile such that no arrow anywhere on the grid points to the Spy, each arrow points to at least one blank on the grid, and no arrow points to any other arrow anywhere on the grid (all diagonals included in both cases). |
||||||||||||||||||||||||||||||||||||||||||||

SafeCracker 50 - a reproduction of a classic design style, from Dave Janelle at Creative CraftHouse. Thanks very much, Dave! Arrange the five layers so that the five numbers appearing in each of the 16 radial columns total 50. There are many vintage paper/cardboard puzzles using this theme - Dave's is made from laser-cut wood and is far sturdier. With the base plate and four additional movable disks, there are 65,536 combinations to try! |
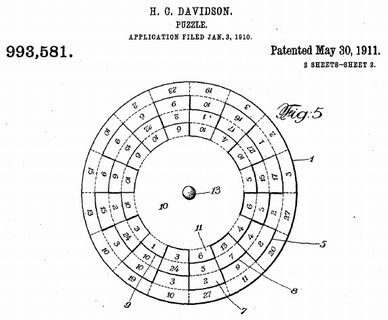
This "SafeCracker" type of puzzle was the subject of U.S. patent 993581, granted to H. Davidson in 1911. But, see below for versions with earlier dates... |
|
The Davidson patent seems to have been applied to the "Great Burglar Puzzle"
which requires columns to
total 40. I obtained the example shown here.
You can see the reference to the patent near the center.
Here is an image of another copy showing an envelope the puzzle evidently came in. (I don't have this.) 
Even earlier, the Hegger's Century Puzzle says "Patent applied for, Copyright 1891 by G. A. Bobrick, New York." (I don't have this puzzle.) G. might stand for Gabriel, since he holds other patents from the late 19th century. Unfortunately I could not find a patent pertaining to the puzzle. While the USPTO website does allow searching for applications (as opposed to granted patents), the database only contains records from 2001 onwards. The USPTO allows one to search for granted patents from 1790 through 1975 but only by issue date, patent number, and current U.S. classification. 

|
|
For reference, here are several more vintage "SafeCracker"-type puzzles:


I obtained an original White Sewing Machine Sixty Puzzle - it says "Copyrighted by A. L. Vandyke 1890." I don't have these:


 Note the swastikas that appear on the
Huntley & Palmers puzzle -
the symbol actually means "that which is associated with well-being" so this likely predates
WWII and the darker usage of the symbol and was probably issued somewhere in the period from 1841
(when Palmers joined Huntley) to 1920 (when the Nazis rose to power).
The "Capture U-Boat 40" puzzle, however, obviously comes from the WWII period.
It was manufactured by the Geiger Bros., Newark N.J.
Note the swastikas that appear on the
Huntley & Palmers puzzle -
the symbol actually means "that which is associated with well-being" so this likely predates
WWII and the darker usage of the symbol and was probably issued somewhere in the period from 1841
(when Palmers joined Huntley) to 1920 (when the Nazis rose to power).
The "Capture U-Boat 40" puzzle, however, obviously comes from the WWII period.
It was manufactured by the Geiger Bros., Newark N.J.
The following photos are from Jerry Slocum's collection, courtesy, The Lilly Library, Indiana University, Bloomington, Indiana. They can be found under classification section 1.3, Miscellaneous Put-Together. 

 "The Jayne Problem" is Copyright 1906 by George H. Vickers.
I don't know what is on the back of the Leinbach puzzle (another sum-to-40 type) or the
"Safe Combination Puzzle" (make all 12 columns sum to 55), but their fronts display no dates.
"The Jayne Problem" is Copyright 1906 by George H. Vickers.
I don't know what is on the back of the Leinbach puzzle (another sum-to-40 type) or the
"Safe Combination Puzzle" (make all 12 columns sum to 55), but their fronts display no dates.


 The Hecker's puzzle says "Pat. applied for" and "Since 1840" so probably dates post 1840, but
displays no other info and I don't know what the back might say.
The Steinfeld puzzle says "Pat. June 20th, 1882" - with a bit of research I found that
the patent in question is
US259920
issued to William H. Reiff of Philadelphia on June 20, 1882.
That makes this the oldest version as far as I know.
The Hecker's puzzle says "Pat. applied for" and "Since 1840" so probably dates post 1840, but
displays no other info and I don't know what the back might say.
The Steinfeld puzzle says "Pat. June 20th, 1882" - with a bit of research I found that
the patent in question is
US259920
issued to William H. Reiff of Philadelphia on June 20, 1882.
That makes this the oldest version as far as I know.
|
|
|
Dave Janelle at
Creative Crafthouse occasionally finds interesting historic puzzles on my website
and creates modern versions, making them available to the puzzling public. Recently he created the 60 Alpha puzzle, based on a design patented in the 1800s.
|
Dave at
Creative Crafthouse
has brought back the 1882 puzzle and issued
the Word Wheel. Thanks for the copy, Dave!

|
Another type of "combination" puzzle relies on a large combinatorial space to be explored, in which one must find particular combinations. An example is this vintage Little Giant Puzzle from the Rogers Novelty Co. of Illinois. Includes four (single-sided) cards, each containing four variations on one quadrant of a caricature of a head - more card sets were offered.




The prototypical example of this type of "puzzle" (or toy) is Ole' Million Face, created by Carey Orr, a Pulitzer Prize winning cartoonist for the Chicago Tribune. It was patented Feb. 3 1925, and was produced in 1925 by the Face Corporation of Philadelphia. The derivative Changeable Charlie was produced in the 1940's (copyright 1948) and onwards. There was also a Changeable Charlie's Aunt.
Ln = n!(n-1)!Rn
| Order n | Enumerator(s) Year |
# Reduced Rn | # Distinct Ln |
| 2 | Euler 1782 |
1 | 2 |
| 3 | Euler 1782 |
1 | 12 |
| 4 | Euler 1782 |
4 | 576 |
| 5 | Euler 1782 |
56 | 161,280 |
| 6 | Fisher and Yates 1934 |
9408 | |
| 7 | Norton 1939 |
16,942,080 | |
| 8 | Wells 1967 |
535,281,401,856 | |
| 9 | Bammel and Rothstein 1975 |
377,597,570,964,258,816 | |
| 10 | McKay and Rogoyski 1995 |
7,580,721,483,160,132,811,489,280 |

The Safari Puzzle by the German company "Pussy" or "Pussycat." A 7x7 Latin Square puzzle presented as a sliding-piece puzzle. Arrange the pieces (7 each of a Hippo, Lion, Elephant, Rhino, Giraffe, Zebra, and Tree) so that only one of each appears in each row and column. |

More Madness by Parker - The Fun and Game Name. No Date. It comes as a single 5x5 plastic sheet, scored with grooves along which you are to break apart the pieces. Each square is one of five colors - yellow, red, blue, green, or white. The unbroken sheet shows the solution - this is a Latin Square puzzle and in the grid, no color occurs more than once in each row or column. There are nine pieces - two are 1x2, seven are 1x3. |

Bird's Puzzle, by Chad Valley. The Bird's Puzzle is very similar to the More Madness puzzle. There are nine pieces, two 1x2 and seven 1x3, colored with five colors - yellow, red, blue, green, and a Bird's logo - to be arranged into a 5x5 grid such that no color appears more than once in each row and column. |

The Missionary Puzzle and Four Others - Five (5) Old Time Puzzles by The Embossing Company of Albany NY. Includes: Missionaries and Cannibals; Staggered Colors; Change About; Double Up; and Sorting Out. |

A vintage French boxed puzzle called Les 15. An order-5 Latin Square. |

Testa Cross Colour Same as Bird's. |
 A vintage cardboard advertising puzzle, "Say Cheese Louder."
Nine pieces to be arranged in a square such that only one of the five symbols appears in each horizontal or vertical line.
A vintage cardboard advertising puzzle, "Say Cheese Louder."
Nine pieces to be arranged in a square such that only one of the five symbols appears in each horizontal or vertical line.
I have highlighted the scored lines separating the pieces. |
||

The "Sudoku 9 Abstract" puzzle from the Plantecs at PuzzleMePlease.com. Form a 9x9 Latin Square using the pieces made from colored woods. |

Utopia issued by Popular Playthings 2009 invented by Sjaak Griffioen Sixteen "buildings" - four each of four different heights. Place on the 4x4 grid according to rules and hints given on 50 challenge cards divided into 25 Phase 1 and 25 Phase 2. I enjoyed Phase 1 but Phase 2 seems overly confusing. (NOTE: this may seem to belong in the Graeco-Latin section, but notice that all buildings of the same height are the same color, so height is really the only differentiator.) |
|



Setko Scramble Arrange the pegs so that no row, column, or main diagonal contains a duplicate letter, and so that "SETKO" is not spelled in any line. |
||
| Aα | Bβ | Cγ | Dδ |
| Cδ | Dγ | Aβ | Bα |
| Dβ | Cα | Bδ | Aγ |
| Bγ | Aδ | Dα | Cβ |

Bali Buttons Requires you to place the sixteen tokens - all combinations of four different shapes with four different colors - on the 4x4 board so that no row, column, or main diagonal contains more than one token with a given shape or color. This is a Graeco-Latin Square puzzle. |

Four Square from the Embossing Company, Albany, NY Combines a Graeco-Latin Square puzzle with two sliding piece challenges.
FIRST.
Place the blocks in the box so that no two of the same number nor of the same color
are in any of the 10 horizontal, vertical, or diagonal lines.
SECOND.
Remove one of the 4's, then, by sliding them about, arrange them in horizontal rows,
each of a different color, and in the order of 1,2,3,4. The fourth or bottom row should be 1,2,3.
THIRD.
After completing the second, slide them about again to arrange them as in second, but in a vertical position.
|

Brain Strain An advertising puzzle consists of sixteen small playing cards - the Jack, Queen, King, and Ace in each suit. As with any Graeco-Latin square puzzle, the objective is to arrange the pieces in a square grid so that neither of the two kinds of feature (in this case, face value and suit) appears more than once in each row, column, or main diagonal. This puzzle was first proposed by Jacques Ozanam. |
||

Quintessence Copyright 1970 by gametime, Inc. of NY, NY A 5x5 Graeco-Latin Square - arrange the 25 pieces in a 5x5 grid such that no row, column, or diagonal contains more than one instance of a circle color or tile color. |


A Floral Derangement - Peterson Games 1972 |

A vintage advertising Graeco-Latin Square puzzle issued by Stephens Motor Works "of the Moline Plow Co., Freeport, Illinois." There are 16 cards: four of each color - orange, purple, green, and yellow; four of each car model - roadster (92), touring (94), touring (96), and sedan (93); and each with a "license number" 1 through 16. The objective is to arrange them in a 4x4 grid such that rows, columns, and main diagonals contain cars of all different models and colors, and the sum of license numbers is 34 in all rows and columns and the four corners, the four centers, and each group of four in a corner! |
||
|
||||


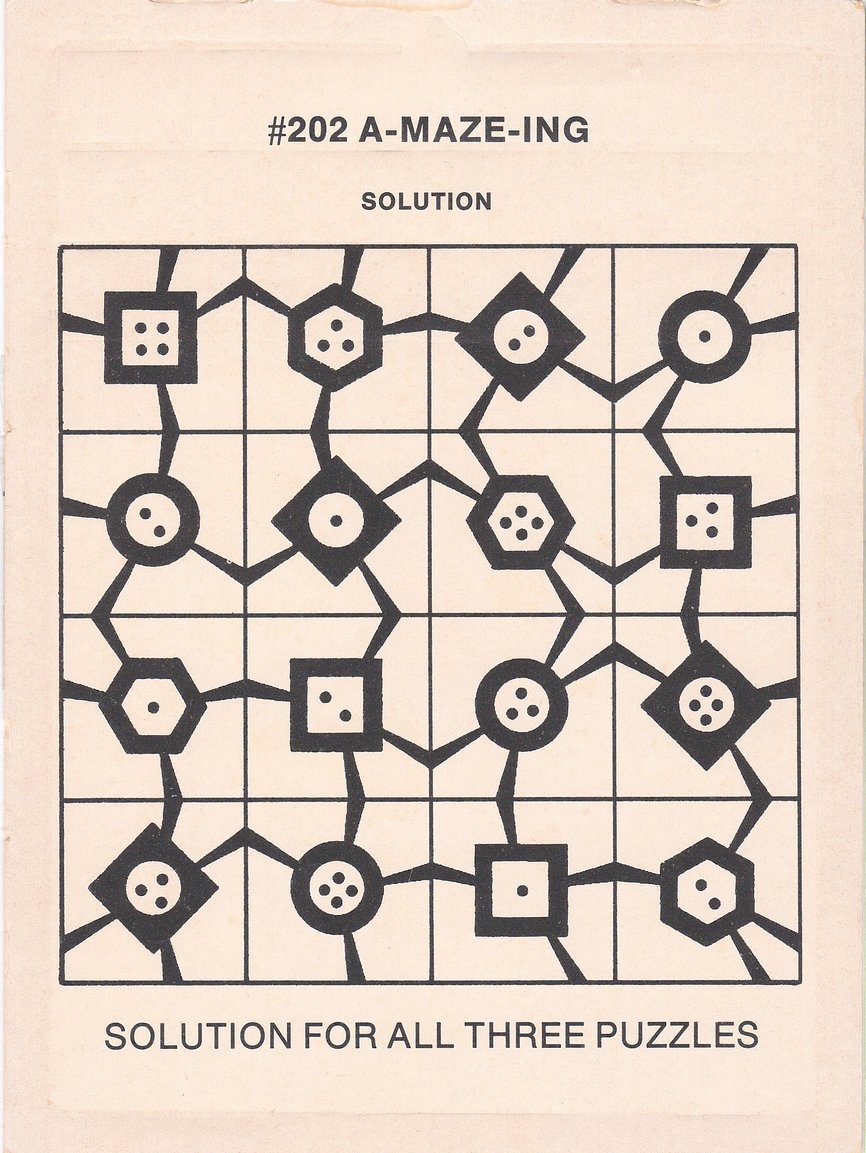
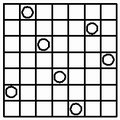
a-maze-ing - a vintage hybrid edge-matching / Greco-Latin Square puzzle, copyright 1975 by H. A. Peterson. Arrange the 16 tiles in a 4x4 grid, first such that the paths match at tile edges, then such that no central shape is repeated in any row, column, or main diagonal, then such that every row, column, and main diagonal contains ten dots, and finally satisfy all constraints simultaneously. If you want to try it yourself, print the solution and cut it into 16 tiles and mix them up. I am pretty sure most folks won't remember the solution offhand! (Right-clicking on an image and opening it in a new tab shows it at enhanced resolution in most cases.) |
||||
| 4 | 9 | 2 |
| 3 | 5 | 7 |
| 8 | 1 | 6 |
Magic Squares exist for all orders except N=2. There is only one distinct Magic Square of order N=3. Supposedly the order 3 magic square was invented in China between 650 and 400B.C. and known as Lo Shu. There are 880 of order 4, and over 275 million of order 5.
In the order 3 normal square, all rows, columns, and the main diagonals total 15. The magic constant for a normal magic square of order n is given by the formula:
Mn = n(n2+1)/2
An order 4 Magic Square appears in Albrecht Durer's famous engraving called Melencolia I:
| 16 | 3 | 2 | 13 |
| 5 | 10 | 11 | 8 |
| 9 | 6 | 7 | 12 |
| 4 | 15 | 14 | 1 |
Each row, column, and main diagonal sum to 34, as do the four corners and the four central cells. Note that this is a solution to Skor Mor's Thinking Man's 34, and Reiss' 34 Skidoo of 1971.

Fascinating 15 - Crestline Crestline put out this order-3 magic square - what could be simpler to manufacture, eh? (I don't have this.) |


Thinking Man's 34 - Skor Mor. Also 34 Skidoo by Reiss, 1971. Sixteen wooden tiles printed with the numbers one through sixteen. Arrange them in a 4x4 grid such that every row and column and main diagonal totals 34. Also find an arrangement in each of 12 distinct classes/patterns. |

Mystifying 65 - Crestline An order-5 magic square from Crestline. (I don't have this.) |
18 17 3
11 1 7 19
9 6 5 2 16
14 8 4 12
15 13 10
|



Pinwheel:27 from Are-Jay Game Company of Ohio |
|

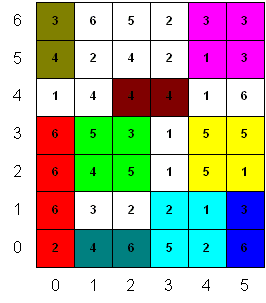 Here is my solution "diary" for the 2nd side puzzle of Catch-21.
Please refer to the diagram at left.
This shows the 6x7 board - the number inside each square indicates the pattern on the board.
The numbers outside the board label the x (horizontal) and y (vertical) coordinate axes.
I will refer to locations on the board via a pair of x and y coordinate pairs.
The tiles consist of the 21 "dominoes" representing all ways of pairing the numbers 1 through 6.
Getting started here is not as easy as for the puzzle on the first side,
since here there are multiple possible locations for every tile.
Begin by considering where the 6/6 tile could be placed - there are only two possibilities:
(0,2)/(0,3) or (0,1)/(0,2) shown in red.
Choose to place it at the latter location. This forces 2/4 to go at (0,0)/(1,0).
Now review possible locations for the 4/6 tile - there were only two possibilities:
(0,2)/(1,2) or (1,0)/(2,0) but the former has been eliminated by our choice of location for 6/6, and
the latter has been eliminated by the forced placement of 2/4.
Ergo we have made an error and must backtrack.
The only decision point is our choice of placement for 6/6, so we must undo everything back to that point
and choose the only available alternative, placing 6/6 at (0,3)/(0,2).
This still precludes one location for 4/6 and forces 4/6 to go at (1,0)/(2,0).
The 2/6 tile must go at (0,0)/(0,1).
Now consider the 6 at location (5,0). It could be covered by either the 2/6 tile or the 3/6 tile, but
2/6 has been used so 3/6 must go at (5,1)/(5,0).
Next consider the 3 at location (0,6). It could be covered by the 3/6 tile or the 3/4 tile, but 3/6 has been used so
3/4 must go at (0,6)/(0,5).
All squares in column 0 have been covered except for (0,4), which now must be covered using the 1/4 tile
at (0,4)/(1,4).
Now look at the 6 at location (1,6).
It could be covered by the 2/6 tile or the 5/6 tile, but 2/6 has been used so the 5/6 tile must go at
(1,6)/(2,6).
This forces us to place the 2/4 tile at (1,5)/(2,5).
Now consider the 6 at location (5,4). It could be covered by 1/6, 3/6, or 5/6, but we have used the latter two
so it must be 1/6 at (4,4)/(5,4).
Now consider the 4/4 tile. The only remaining possible location for it is at (2,4)/(3,4).
Likewise consider the 1/1 tile. It can only go at (3,3)/(3,2).
Next consider the 5 at location (4,3). Either way it must be covered by the 5/5 tile.
This implies that the 1/5 tile must be aligned next to it. There are two ways of placing them and either is OK.
Consider the 1 at location (4,1). Either way, it must be covered by the 1/2 tile. This implies that the
2/5 tile must be aligned next to it. There are two ways of placing them and either is OK.
Now look at the 2 at location (2,1). Since the 2/5 tile is used, we must use the 2/3 tile here.
Next consider the 4 at (1,2). Either way it must be covered by the 4/5 tile and the 3/5 must be aligned next to it.
There are two ways of placing them and either is OK.
There remains only 1 location for 2/2, at (3,6)/(3,5).
Lastly, consider the 3 at (5,6). It must be covered by the 3/3 tile and the 1/3 must be aligned next to it.
Again, two arrangements are possible and either is OK.
Here is my solution "diary" for the 2nd side puzzle of Catch-21.
Please refer to the diagram at left.
This shows the 6x7 board - the number inside each square indicates the pattern on the board.
The numbers outside the board label the x (horizontal) and y (vertical) coordinate axes.
I will refer to locations on the board via a pair of x and y coordinate pairs.
The tiles consist of the 21 "dominoes" representing all ways of pairing the numbers 1 through 6.
Getting started here is not as easy as for the puzzle on the first side,
since here there are multiple possible locations for every tile.
Begin by considering where the 6/6 tile could be placed - there are only two possibilities:
(0,2)/(0,3) or (0,1)/(0,2) shown in red.
Choose to place it at the latter location. This forces 2/4 to go at (0,0)/(1,0).
Now review possible locations for the 4/6 tile - there were only two possibilities:
(0,2)/(1,2) or (1,0)/(2,0) but the former has been eliminated by our choice of location for 6/6, and
the latter has been eliminated by the forced placement of 2/4.
Ergo we have made an error and must backtrack.
The only decision point is our choice of placement for 6/6, so we must undo everything back to that point
and choose the only available alternative, placing 6/6 at (0,3)/(0,2).
This still precludes one location for 4/6 and forces 4/6 to go at (1,0)/(2,0).
The 2/6 tile must go at (0,0)/(0,1).
Now consider the 6 at location (5,0). It could be covered by either the 2/6 tile or the 3/6 tile, but
2/6 has been used so 3/6 must go at (5,1)/(5,0).
Next consider the 3 at location (0,6). It could be covered by the 3/6 tile or the 3/4 tile, but 3/6 has been used so
3/4 must go at (0,6)/(0,5).
All squares in column 0 have been covered except for (0,4), which now must be covered using the 1/4 tile
at (0,4)/(1,4).
Now look at the 6 at location (1,6).
It could be covered by the 2/6 tile or the 5/6 tile, but 2/6 has been used so the 5/6 tile must go at
(1,6)/(2,6).
This forces us to place the 2/4 tile at (1,5)/(2,5).
Now consider the 6 at location (5,4). It could be covered by 1/6, 3/6, or 5/6, but we have used the latter two
so it must be 1/6 at (4,4)/(5,4).
Now consider the 4/4 tile. The only remaining possible location for it is at (2,4)/(3,4).
Likewise consider the 1/1 tile. It can only go at (3,3)/(3,2).
Next consider the 5 at location (4,3). Either way it must be covered by the 5/5 tile.
This implies that the 1/5 tile must be aligned next to it. There are two ways of placing them and either is OK.
Consider the 1 at location (4,1). Either way, it must be covered by the 1/2 tile. This implies that the
2/5 tile must be aligned next to it. There are two ways of placing them and either is OK.
Now look at the 2 at location (2,1). Since the 2/5 tile is used, we must use the 2/3 tile here.
Next consider the 4 at (1,2). Either way it must be covered by the 4/5 tile and the 3/5 must be aligned next to it.
There are two ways of placing them and either is OK.
There remains only 1 location for 2/2, at (3,6)/(3,5).
Lastly, consider the 3 at (5,6). It must be covered by the 3/3 tile and the 1/3 must be aligned next to it.
Again, two arrangements are possible and either is OK.
 You can make and play this type of puzzle with just some paper and a set of dominoes.
Wonder Workshops had this inexpensive version of a domino puzzle (I don't have it).
An arrangement of pips is presented on a card. Using a set of dominoes, cover the card by matching
pairs.
You can make and play this type of puzzle with just some paper and a set of dominoes.
Wonder Workshops had this inexpensive version of a domino puzzle (I don't have it).
An arrangement of pips is presented on a card. Using a set of dominoes, cover the card by matching
pairs.

Other good resources for Domino Puzzles:
 One of the earliest mechanical puzzles I ever had was an Instant Insanity
given to me by my mother.
(Thanks, Mom! BTW, this puzzle obsession is all your fault!)
Instant Insanity was invented by
Franz O. (Frank) Armbruster, a California computer programmer,
and marketed by Parker Brothers during 1966-67. It sold about 12 million copies.
I have an original from Parker Brothers, and copies from Winning Moves (found in a shop in Mystic) and Kadon.
There are many puzzles in what I call the "Instant Insanity Family."
Typically, the puzzle comprises four colored cubes. Four colors are used, and each of the cubes' faces are colored with one of the four colors.
The objective is to find a linear arrangement of the cubes (a rectangular prism) such that all four long sides
show each color only once.
The faces on the ends and in between cubes don't matter.
There are 41,472 distinct ways to line up the four cubes, so exploring them all by hand will take a while!
One of the earliest mechanical puzzles I ever had was an Instant Insanity
given to me by my mother.
(Thanks, Mom! BTW, this puzzle obsession is all your fault!)
Instant Insanity was invented by
Franz O. (Frank) Armbruster, a California computer programmer,
and marketed by Parker Brothers during 1966-67. It sold about 12 million copies.
I have an original from Parker Brothers, and copies from Winning Moves (found in a shop in Mystic) and Kadon.
There are many puzzles in what I call the "Instant Insanity Family."
Typically, the puzzle comprises four colored cubes. Four colors are used, and each of the cubes' faces are colored with one of the four colors.
The objective is to find a linear arrangement of the cubes (a rectangular prism) such that all four long sides
show each color only once.
The faces on the ends and in between cubes don't matter.
There are 41,472 distinct ways to line up the four cubes, so exploring them all by hand will take a while!

 The number of ways to color a cube, allowing repeated colors, with at most k colors is given by
Polya's Enumeration Formula,
which follows from
Burnside's Lemma.
The formula for a cube is:
The number of ways to color a cube, allowing repeated colors, with at most k colors is given by
Polya's Enumeration Formula,
which follows from
Burnside's Lemma.
The formula for a cube is:
This gives the following values for k=2,3,4,... (Sloane's integer sequence A047780):
10, 57, 240, 800, 2226, 5390, 11712, 23355, 43450... So for four-color type puzzles such as Instant Insanity, there are 240 possible cubes to choose from when creating the puzzle. The trick is to find a set that guarantees a solution, and preferably only one solution! The cubes are typically diagrammed by "unfolding" them and representing them as a cross:

Note that when coloring a cube, once you've colored two pairs of opposing faces, then given colors for the last pair of opposing faces, you define a pair of mirror image cubes by assigning the colors to those two remaining faces in one way or the other. For purposes of this type of puzzle, mirror image cubes are identical and distinctions between them are immaterial to the solution.
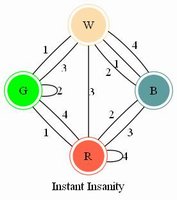 Ivars Peterson's MathTrek article of August 9, 1999, "Averting Instant Insanity," is devoted to graphical solution techniques
pertaining to this type of puzzle.
Ivars Peterson's MathTrek article of August 9, 1999, "Averting Instant Insanity," is devoted to graphical solution techniques
pertaining to this type of puzzle.
Here is my copy of the solution letter sent out by Parker Brothers on request:

| The Schossow / Katzenjammer Puzzle | ||
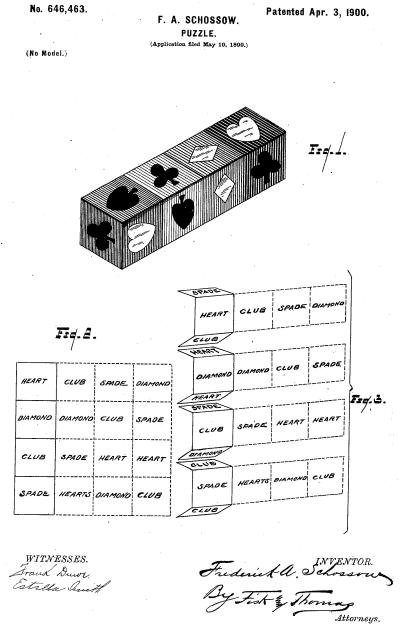
|

|
|
Here is a graph of the Katzenjammer puzzle, side-by-side with the graph for Instant Insanity:
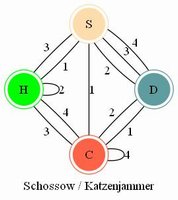

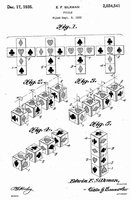
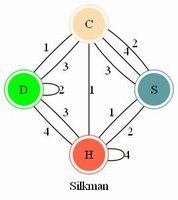
|
||
|
So, how does one establish that two such puzzles are in fact isomorphic? Well, I read up on the Graph Isomorphism Problem mentioned previously, and found references to nauty by Brendan McKay, which is evidently the best publicly available software. However, it seems like overkill for my purposes. One also needs a way to represent graphs as data - there seem to be two good standards, DOT and GXL. I've chosen DOT since the graphviz package is handy. I categorize these puzzles by a numeric shorthand: the number of faces per element, the number of elements, and the number of colors/symbols in total. II-type (Instant Insanity - type) puzzles, with 6 faces per cubic element, four cubes, and four colors, are (6,4,4) in my scheme. (6,4,4) puzzles are represented by pseudographs having exactly four nodes and exactly twelve labeled, undirected edges. For now I'll omit puzzles with fewer or more cubes, non-cubes, and fewer or more symbols/colors. Many approaches to graph isomorphism entail establishing some way to convert a graph to a canonical form, and showing that two graphs with the same canonical form are in fact isomorphic. Another useful concept is the invariant - some property of a graph, that all graphs isomorphic to it must share - e.g. the number of nodes. Obviously, two invariants that apply here are four nodes and twelve edges. One can also try to define a complete or sufficient invariant which completely decides isomorphism - the number of nodes and edges doesn't meet this need. Yet another useful concept is the signature or certificate of a graph - a way of assigning a coded ID to the graph as a whole, that plays the role of a sufficient invariant. I've come up with what I believe is a good way of assigning certificates to II-type puzzles. First, encode the nodes using four hex digits (0-F) based on their connectedness: The rightmost or least significant place counts the number of self-loops on the node. The other three places give the counts of connections to the other three nodes in no particular order, but sorted in increasing value from left to right. For twelve-edge graphs, we really only need up to digit 'C' and in practice most counts are only as high as 3. For the II/SK puzzle, the four node codes are: 0221 (the green or heart node), 0230 (the blue or diamond node), 1221 (the red or club node), and 1230 (the white or spade node). This is convenient since each node gets a unique code. Next, encode the cubes themselves, each as a series of six node-codes derived previously - remember, an edge on the graph was defined by a pair of opposing faces on the cube. So an edge can be encoded with 8 digits by concatenating the codes for the two nodes it connects, sorted in lexicographic order (the edges are undirected, after all). And, a cube can be represented with 24 digits by concatenating the codes for the three edges it contributes to the graph, again sorted. These two sorting steps mean that we lose info to distinguish mirror image cubes, but as previously established, that doesn't matter to the solution! Finally, the whole puzzle's 96-digit certificate is the four codes for the cubes, again sorted. And here again, the sorting doesn't matter, since the order of the cubes doesn't matter to the solution. For the both the Instant Insanity puzzle and the Schossow/Katzenjammer design, this certificate is (shown with some punctuation to aid understanding):
02211230023012300221122102301230 12211221022112300230122112211230 |
||

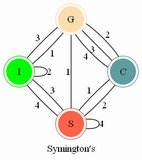
This is a vintage advertising premium called Symington's Puzzle. It contains four cardboard cubes, each with a different arrangement of four Symington's product advertisements on their faces: Soup, Custard Powder, Ideal Cream, and Gravy. It is shown in Slocum and Botermans' "Puzzles Old & New" on page 38. Isomorphic to SK. |

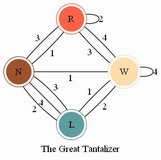
The Great Tantalizer Isomorphic to SK. |

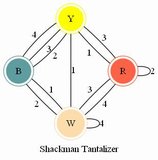
Tantalizer - Shackman #7415 Isomorphic to SK. |
|||

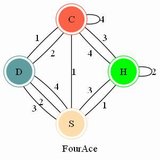
Here is another vintage cube matching puzzle called The FourAce Puzzle. The four wooden cubes are decorated with various arrangements of the four playing card suite symbols: hearts, diamonds, clubs, and spades. The box says "Provisionally Protected" but does not identify the manufacturer or date of manufacture. According to Slocum, this puzzle was sold in Britain at Gamage's in 1913. Isomorphic to SK. |

An advertising version of the Tantalizer puzzle, from Bass. |
I am not sure what this puzzle is actually called, but on the bottom of the tray it says "Masudaya Made in Hong Kong" so I call them the Masudaya Cubes. This may be the same as Ideal's Face Four puzzle, which I also found. 
Ideal's Face Four - Celia Seide (a German collector) notes that in Germany these are known as "Trikki 4." |
|||

Logi-Qubes |

Those Blocks |

Krazi Kubes |
|||

Taktikolor |

Devil's Dice - Pressman |

Devil's Dice - made in Hong Kong No.104A |
|||

Daffy Dots - Reiss 1971 |

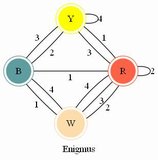
Enigmus Not isomorphic to SK. |

Logicubes by Kaufmann / Galil Isomorphic to SK. |
|||



"Can you solve those Damblocks?" were offered by the Schaper Manufacturing Company, Minneapolis, Minn. in 1968. I have examples in red, white, and black. |


I got Mutando by Logika at Games People Play, and Mutando II from Time Machine Hobby. |
||||

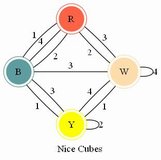
Nice Cubes Isomorphic to SK. |

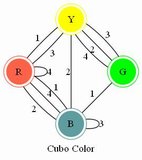
The vintage Cubo Color Puzzle. Not isomorphic to SK. |

Coloured Cubes Peter Pan Series Regd. |
|||

Color Cubes |

Crazy Blocks Color Puzzle Created for Jak Pak Inc. of Milwaukee Made in British Crown Colony of Hong Kong |

Levenger Cubes |
|||
|
|||||

Idiot's Delight - Field Mfg. Co. Inc. NY Cube set signature 01143639 - Isomorphic to SK |

Suits Me - Steve Kelsey Arrange the four cubes in a row such that all four long sides show each suit once. (Eq. to SK) |
||||
|
There can be more than four cubes and four colors... |
|||||

The Allies Flag Puzzle is another very old example of this family. This puzzle has five cubes, and each cube has some arrangement of five flags on its faces. According to Slocum, this puzzle was sold in Britain at Gamage's in 1915. |


Dorobo - Hanayama |

Hlavolam Iribako |
|||
This is Meffert's "Drives You Crazy." It includes six cubes instead of the usual four. |

six cubes |
||||
|
The pieces aren't always cubic... |
|||||

This is the Masudaya Hexagon Mind Exerciser. It has six hexagonal pieces. The objective is to line up the six hexagons so that each of the six rows of six faces shows all six colors. Unlike a set of cubes, where on each cube two faces are not used in a solution, here all six faces of every hexagon will be used. This means that there must be in total six faces of each of the six colors. In my copy of the puzzle, all six hexagons have distinct color arrangements - i.e. there are no duplicate pieces. I have found at least one solution - one can employ the graphical technique, but not in exactly the same way as for cubic puzzles - here, three mutually consistent sub-graphs are needed, and they are not independent. |
A vintage Cylinder Ten by Masudaya. Ten rotating disks each with ten color segments. The English instructions say, "Arrange 10 different colors in a line to get all rows correct. The probability of getting the correct order is one in a billion. This puzzle will give the whole family hours of amusement. Note: it is packed in the factory with colors in the correct order (i.e. the solution)" There is no date I can find on any of the material. However, I translated "Cylinder 10" into Japanese and did a search on Google Japan just to see what would turn up, and I found a "FrogPort" blog article from April 2008 talking about the release of this puzzle and how it is in a series with Masudaya's other puzzles Face 4, Hexagon Mind Exerciser, and Circus 7. Here is a link to the blog via google translation to English. The instructions say "10 different colors in a line" but do NOT stipulate that the SAME ten colors must be in every line! This is unlike the traditional Instant Insanity type where one of each color must be present. This allows the rotating disks to have repeated or missing colors. A "line" is a row of stickers across all ten disks. There are ten disks each with ten positions/stickers, so they are accurate in saying one in a billion, since there are 10^9 possible settings (the setting of the first disk is immaterial). |


Go Crazy Embree Manufacturing Co. NJ 1969 Arrange the five disks so that alternate rows have five different colors, then three different colors. The five disks are separate and may be removed from the case and re-ordered. |
|||

The Buvos Golyok is a clever variant using balls enclosed in a tube. |


Bognar Planets (Bolygok) - brown, white |

Hungarian Tactics |
|||
Stan Isaacs sent me examples of his Doctor Octo and Dr. High Octane puzzles.
These versions use octahedrons rather than cubes,
and a clever mirrored base to allow one to see all faces.
Thanks, Stan!


|
|||||
|
The cubes are usually labeled with colors, but sometimes numbers are used... |
|||||

Twenty Teazer Arrange the cubes so that each side totals 20. |


Crazy Cubes |

Tantalizing Ten - Shackman |
|||
|
|||||

Kathy's Kubes by R. Gee Arrange so dots total 10 on each long side. |
|||||
|
Steiffel Tower |

Totemania |

Match 'Em High - Roads |

Match 'Em High - Pipes |



MindBlocks - issued by Play With Your Mind, Inc. of Long Beach California Copyright 1989 by Jeff Merrill and Myron Nickerson One of the puzzles, called "Conceptual Block" calls for you to make a 2x2x2 cube such that each side has four matching shapes. |
|||
[60]
I used the graphical technique to solve Nice Cubes:
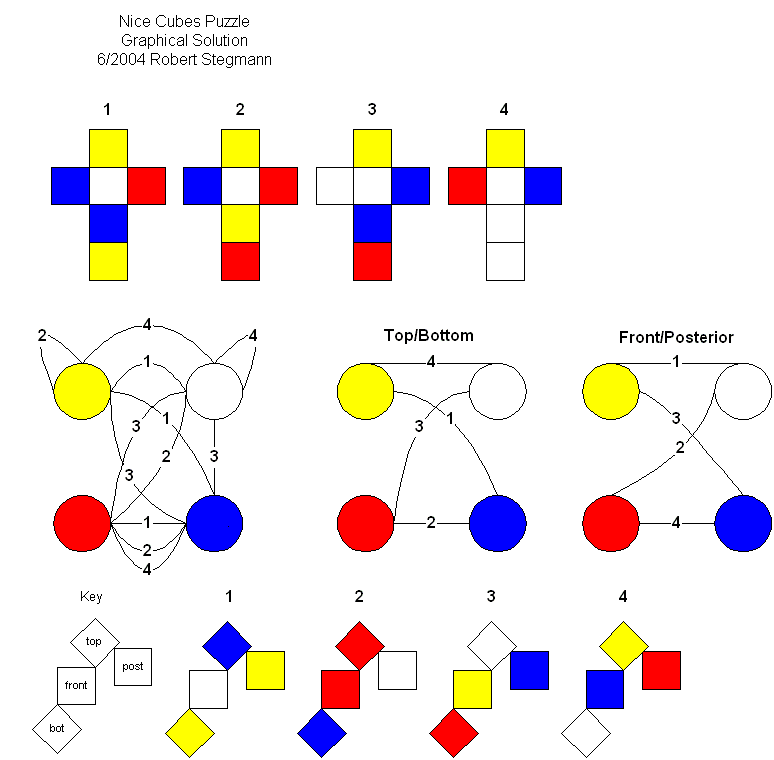
Below is my solution to the Masudaya Cubes, using the graphical technique. The connectivity of this graph is similar to that of the Nice Cubes, though its edges seem differently labeled. Are the puzzles in fact isomorphic?
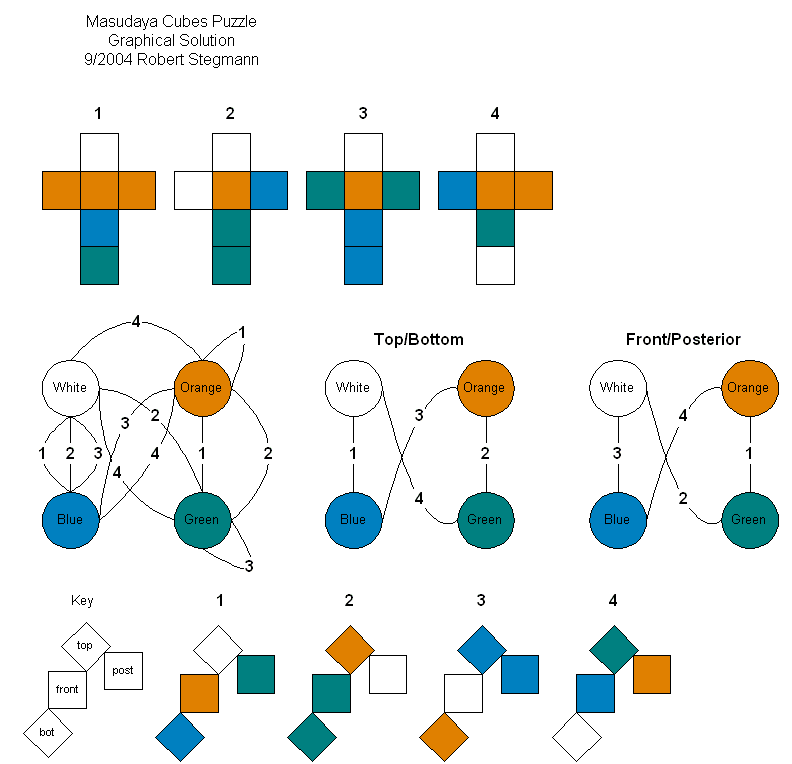
Recall that there are 240 ways to color a cube using 4 colors. Given a "stable" of 240 cubes from which to choose four, how many possible 4-cube sets are there? To allow repeats but eliminate sets that are identical (since the ordering of the 4 cubes does not matter), we use the formula for a multicombination:
(n+k-1)_C_k
In our case, n=240 and k=4, (240+4-1)_C_4 = 141,722,460. So, we've got over 140 million sets to explore! Also, for a set of 4 cubes, there are 41,472 possible ways to arrange them - that's going to be a lot of work.
But we can reduce this by eliminating from consideration all cubes that do not have at least one face of each color. It's a little arbitrary, and it means my conclusions are not universal over the entire universe of possible puzzles, but I think it's reasonable - most commercial puzzles comply. Of the 240 possible four-color cubes, there are 68 that use all four colors at least once each. Each cube can be represented by a four-node, 3-edge pseudograph, where the nodes are the four colors symbolized by the letters ABCD and each edge corresponds to a pair of opposing faces on the cube. The graphs are the same for mirror-image cubes, since the edges are undirected. The 68 cubes give rise to only 52 unique graphs. Those 52 graphs can be grouped into 6 groups - each group is closed with respect to a permutation of the node/color assignments, of which there are 24 (4!). Below is a chart I made identifying the 52 graphs/cubes by unique ID number (00-51) and a small diagram showing the 3 edges. The colors identify the six groups. It should be easy to construct a cube given its little diagram and the key on the lower right. You just have to decide on your assignment of actual colors to ABCD, and then be sure to remain consistent.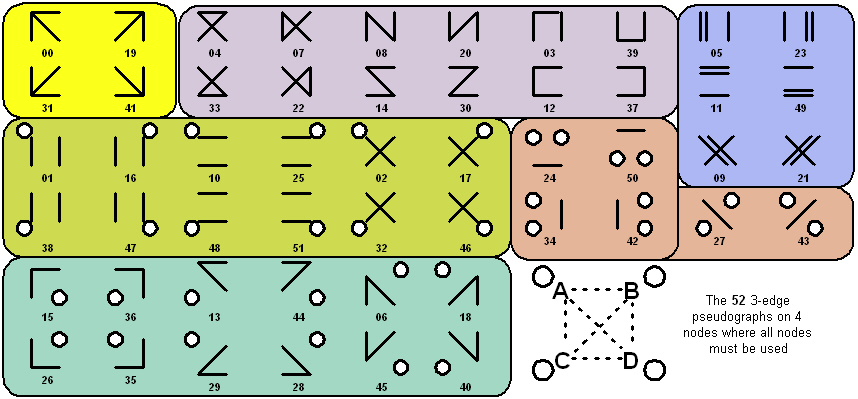 Rick Eason worked on this problem, too, after we talked at NYPP2010.
Rick Eason worked on this problem, too, after we talked at NYPP2010.
|
|



0) 132647 00010203 1) 5160 00010218 2) 21186 00010234 3) 3428 00010329 4) 38466 00010318 5) 2088 00011839 6) 8070 00011631 7) 612 00031631 8) 28626 00010518 9) 702 00032939 10) 3276 00012039 11) 282 00031839 12) 7310 00011639 13) 312 00032637 14) 1380 00032651 15) 144 00033539 |
16) 9060 00012750 17) 120 00033139 18) 360 00032039 20) 1980 00032549 22) 111 00052039 23) 12 03082645 24) 2340 00032338 26) 204 00162238 27) 1 00193141 28) 486 00033847 29) 18 00194045 30) 30 00163147 32) 1188 00051639 34) 18 01163246 36) 114 01033839 |
40) 420 00163841 44) 156 01030539 48) 94 00274250 52) 12 01164045 53) 3 06184045 54) 6 01283844 56) 96 01063847 60) 6 03113949 64) 120 01030523 72) 51 01032338 80) 3 24274350 96) 12 01233438 128) 6 03052339 140) 3 01163847 160) 6 01052338 |
01 04 20 40 01 14 36 39 02 03 22 45 02 12 33 44 03 07 17 40 03 14 26 47 03 30 35 38 04 08 16 45 |
04 12 28 32 04 29 37 46 06 20 33 47 06 22 32 39 07 10 28 30 07 14 44 48 07 18 39 46 08 10 26 37 |
08 12 36 51 08 18 33 38 12 20 25 35 13 17 33 37 13 22 30 51 14 22 25 29 15 16 30 39 15 20 37 48 |
00 03 04 19 00 03 04 20 00 03 04 30 00 03 04 31 |
00 03 04 39 00 03 14 19 00 03 14 20 00 03 14 22 00 03 14 37 |
00 03 14 39 00 03 14 41 03 04 08 12 03 04 12 20 |
The table below lists, in (mostly) alphabetical order (I tried to keep sequels together), those I know of and shows images where I either have a copy or have been able to find pictures. I don't have them all and I will note the ones I don't have. Those I have are highlighted like this. Those I do not have are highlighted like this.
I would like to acknowledge the following:
|
Bananas

Bananas 1982 Onsworld Ltd. "Arrange cubes to show four complete bananas each with a label." There are four cubes, and four types of side: a banana tip, stem, middle segment with no label, and middle segment with label. Unlike a standard II-type puzzle, the images have distinct orientations which must be respected to form the complete bananas. The tips, stems, and middle segments must all be aligned properly. A little analysis reveals that the usual four-in-a-row arrangement of the cubes cannot satisfy the goal - but then, the objective does not stipulate that arrangement, does it? |
Bananas II

Bananas II |
Blue Movie

Blue Movie - 1986 Wellingtons I don't have this. |
Body Job

Body Job - Onsworld I don't have this. |
|
Boob Cube

Boob Cube - Wellingtons I don't have this. |
Booby Trap

Booby Trap - 1986 Wellingtons I don't have this. |
Bunkered


Bunkered 1987 Wellingtons "Tee-off by placing the cubes together then rearrange them to show, simultaneously, TWO identical golf courses." |
The Cat Puzzle

The Cat Puzzle - Wellingtons I don't have this. Image from Jim Storer's collection. |
|
Cash 22

Cash 22 - Wellingtons 1992 |
Computer Challenge
 Computer Challenge - 1984 Wellingtons Computer Challenge - 1984 Wellingtons
I don't have this. |
Computer Magic Square Challenge


Computer Magic Square Challenge 1995 Images & Editions |
Computer Word Challenge

Computer Word Challenge - 1985 Wellingtons I don't have this. |
|
Crossword Cubes



Crossword Cubes - 1989 Wellingtons I don't have this. Here is a possible alternative package: 
|
Cubix 3D



I don't have this, but see Rebus in the Pattern Blocks section below. |
||
|
Cuss

Cuss 1980 Onsworld Ltd. "Simply arrange the blocks in a row so that each side carries a dictionary four letter word, all reading from left to right. No foreign words or proper names allowed. A clue in case you get stuck and a solution are included." "This is one of a unique range of cube puzzles devised for Onsworld by Stephen Leslie. The series includes Cuss, Diabolical, Footsie, Frantic, Son of Cuss, and Walk Up." |
Son of Cuss

Son of Cuss 1982 Wellingtons Devised by Stephen Leslie "Arrange the cubes to show at least 24 different four-letter (dictionary) words." |
Diabolical

Diabolical (Onsworld) "Arrange the dice in a row so that the four long sides all carry the same total number of spots." Multiple solutions exist - the set of addends doesn't have to be same for each side. |
Double Cross

Double Cross Wellingtons 1991 |
|
Fascinating Felines



Fascinating Felines - 1993 Wellingtons |
Footsie

Footsie 1982 Wellingtons "Arrange the four cubes in a square so that wherever the surfaces of two cubes join (top, bottom, and sides) pairs of feet are formed." Devised by Stephen Leslie. |
Frantic

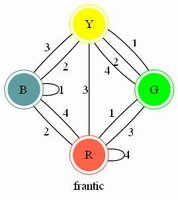
Frantic 1980 Onsworld Ltd. "Place the four cubes in a row and simply rearrange them so that one of each colour shows on each long side." Devised by Stephen Leslie. Isomorphic to SK!
I also have Brainstorm by Onsworld which looks the same...
|
Frantic (alt.)

An alternative version of Frantic, with solid colors. Colin says it is the same graph. 
Also issued with black backgrounds. |
|
Frantic II

Frantic II "Place the cubes together in a square so that wherever they meet, top, bottom, and sides, the coloured squares match." Frantic II was invented by Dr. Kenneth Miller. |
Golf

Golf - Wellingtons "Places the cubes together to show the word GOLF four times. The letters must all point the same way. Try it - then baffle them at the 19th." |
Golf Crazy


Golf Crazy - Wellingtons |
Grandstand


I don't have this. |
|
The Great British Puzzle

The Great British Puzzle - 1997 Images & Editions |
The Kitten Puzzle


The Kitten Puzzle - 1999 Images & Editions by Dr. Kenneth Miller |
Knickers

Knickers - Wellingtons I don't have this. "Arrange the knickers in a line so that there is one of each colour on each long side - they can be in any order and face any direction." |
Marilyn - The Eternal Puzzle


Marilyn - The Eternal Puzzle - 1989 Wellingtons |
|
Match of the Play


Match of the Play 1989 Wellingtons "Solve the puzzle by placing all six cubes together so that both sides show a player being tackled." |
Monkey Business Spring Fever

Monkey Business Spring Fever - Wellingtons I don't have this. |
Nuts

Nuts 1982 Wellingtons "Place the four cubes in a row and simply rearrange them so that one of each kind of nut shows on each long side." Isomorphic to SK! |
180 Top Dart

180 Top Dart 1990 Wellingtons "Place the cubes in a straight line so that all four long sides add up to the magic number... one hunder and eighty!" There are six cubes, and the following 12 symbols appear: inner bullseye (50 pts), triple 2 (6 pts), double 3 (6 pts), triple 4 (12 pts), double 6 (12 pts), 9, double 9 (18 pts), triple 9 (27 pts), 12, double 17 (34 pts), 18, triple 20 (60 pts). |
|
The Pig Puzzle


The Pig Puzzle Images & Editions |
Poker Puzzle

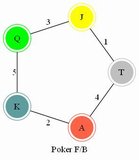
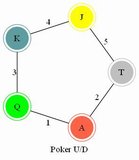
Poker Puzzle 1987 Wellingtons "Place the dice in a line so that one of each design appears on each of the four long sides - the order and directions of the designs are not important." There are 5 cubes. The designs are: 10, Jack, Queen, King, Ace. I received an email from Alvaro Ledesma back in 2016 and he informed me that this set has two solutions - "the second solution has the same UD solution but the FB is made of a different set of axis." Can you find Alvaro's second FB solution? Interestingly, back in 2015, Mike Beeler informed me that he had found another solution, where "F/B = same as yours; U/D = T -5- J -2- Q -4- K -1- A -3- T." |
Rugby

Rugby - 1995 Images & Editions - Dr. Kenneth Miller Two puzzles based on the two versions of Rugby - for the Rugby League fan, place the cubes in a straight line so that each long side shows exactly 13 pieces of muddy lace. For the Rugby Union fan, place the cubes in a straight line so that each long side shows exactly 15 pieces of muddy lace. I don't have this. |
|
|
Seams Impossible

Seams Impossible - 1986 Wellingtons I don't have this. "Place the cubes in a square so that wherever two cubes join (top, bottom, and sides) complete legs are formed." |
Snookered

Snookered - Wellingtons "Place the cubes together in two rows of four, to make a snooker "table." Then rearrange them to show three sets of snooker balls: one on the top, one on the bottom, and one on the four sides of the "table." A set of snooker balls comprises: 15 reds and one each of white, black, pink, blue, brown, green, and yellow." |
Snookered Again

Snookered Again - Wellingtons "Arrange the cubes in a block (two rows of three) so that one, and only one, of each of the eight colours shows on the top, sides, and base of the block." |
Soccer


Soccer - "You may need extra time!" Appears in a box and a blister package. Images & Editions 1996 - designed by Dr. Kenneth Miller Thanks to Rob Hegge for photos. |
|
Soccer



Soccer Puzzle - "Make it your Goal" - Wellingtons 1987 |
Spellbound

Spellbound |
Spellbound (alt.)

Spellbound - alternative version - Onsworld Ltd. 1980 |
Suit Yourself

Suit Yourself 1990 Wellingtons "Place all six cubes together in a block of two rows of three to show (on top, bottom, and sides) a full pack of 52 cards with no duplicates." |
|
Tantalizer
Crossword 


I don't have this. This and the other Tantalizer puzzles seem to be more dexterity than Insanity-type. |
Tantalizer
Frustration 
I don't have this. (Photo from Slocum collection.) |
Tantalizer
Jet Set 
I don't have this. (Photo from Slocum collection.) |
|
|
Top Dart


Top Dart |
Total Distraction

Total Distraction 1988 Wellingtons "Put the cubes together to form one large cube with all rows, columns, and diagonals having the same total: 99." |
Walk Up

Walk Up 1980 Onsworld Ltd. "Place the four cubes on top of each other in a column. Arrange cubes so that ladybird (sic) tracks reach from top to bottom on all four sides. Ladybirds need not point all the same way." Devised by Stephen Leslie. |
Watch It

Watch It - 1998 Images & Editions I don't have this. |
|
World Puzzle


World Puzzle - Wellingtons I don't have this. |
|||
[29/56]
The Lagoon Group also has offered 4-cube puzzles...


The most frequently mentioned, most dating from 1969, are:
|
Less often mentioned, dating from 1970 and 1971, are:
|
|
|||||
|
The Perfect Square 1969 #505 Assemble a square using 12 pieces - like colors must not touch. |

The Tricky Triangle 1969 #505 Using 10 barbell-shaped pieces composed of two linked circles each, and one single circle, build an edge-6 equilateral triangle (of 21 circles) such that "no two circles of the same color are in the same line of the triangle." Each circle is 1 of 6 colors. The Tricky Triangle puzzle by Waddingtons is a 2-dimensional analogue of Oops Again. |
The Perfect Circle 1969 #505 Assemble a circle from 16 pieces in 4 basic shapes and 3 different colors, such that like-colored pieces don't touch. |
|||

The Wobbly Web Copyright 1969 No. 505 Create a rectangle from the 15 square tiles such that web strands join (edgematching). JH Vol.2 p210 |

The Perplexing Pyramid 14 square tiles each of which has a colored circle in each corner. Create a "pyramid" of cards - a 3x3 base, then a 2x2 layer, then one card on top - layers must align over spots, and spot colors must match vertically. |

The Reluctant Rectangle 1970 #345 Form a rectangle from the 12 3x2 L-shaped pieces such that no two pieces of the same color touch in any way. There are 3 pieces each of four colors. All the pieces are "normally-handed" L's except for two of one color are reversed. |
|||

Little Circles 1970 #346 Pack 18 pieces formed from circles into the box. (The instructions are printed on the box, and there is no mention of a color-dismatching constraint.) No Pamphlet. |

Coloured Square 1971 #340-E Form a square from 12 L-shaped colored tiles such that like colors don't touch. |

Rectangle Tangle 1971 #340-F Form a rectangle with a bi-color perimeter from the 10 tri-color and 2 bi-color L-Trominoes. |
|||

Beat the Elf - by House of Games Corp. Ltd. Don Mills, Ontario 1970 Build a 3x3x3 cube with the 13 blocks so that no face shows three squares in a row of either color, horizontally, vertically, or diagonally. There are 11 1x1x2 blocks of 1 light and 1 dark. There is one 1x1x2 block of two darks. There is one 1x1x3 block of two lights (adjacent) and 1 dark. |

Kolor Kraze - by House of Games Corp. Ltd. Don Mills, Ontario 1970 Discussed in Slocum and Botermans' Puzzles Old and New on page 43. The Kolor Kraze puzzle consists of 12 dicubes and a tricube, each made of differently colored cubes. There are 3 each of 9 different colors. As in the Gram's Cube, the goal is to create a 3x3x3 cube from the pieces, such that each of the 9 colors appears only once in each of the six faces of the cube. Sivy Fahri wrote an article about the Kolor Kraze and the Nine Color Puzzle called "Nonahuebes" he developed based on it. A PDF of Fahri's article is available at the Gathering 4 Gardner Wiki. |

Cube Fusion Alright, it's a game not a puzzle, but I remembered these pieces from my childhood and now I know what they belonged to! |
|||

Gram's Cube was made by Gram Toys of Birkerod, Denmark. The puzzle consists of 27 Lego-like cubies that mate side-to-side as well as up-and-down. There are 3 cubies each of nine different colors. The objective is to construct a 3x3x3 cube such that each side shows all 9 colors. At first I thought a trick was necessary, but I found a solution using all 27 cubies. I picked this up in a trade with Norman Sandfield, at the January 2005 New York Puzzle Party. |


Level Q, by Eng's IQ Co. Ltd. 1987 Hong Kong. I purchased this quite some time ago. Level Q consists of a hexagonal board and twelve bar-bell shaped pieces. There are three challenges - first, build seven stacks of six disks each. Next, again build seven stacks of equal height, but such that one bar lies on each side of the hexagon and on each of the six spokes. Finally, satisfy the constraints already mentioned, and also ensure that each stack contains only one of each color disk. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


The Trapagon and Magzphere Six pieces interlock - arrange them so that there are five different colors on each "face." |


The object of Oops Again is to build a pyramid with the 2-sphere pieces so that no two spheres of the same color touch at all. The Golf Smarts Pyramid (a gift from Brett) is similar. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

Tetraball - designed by John Conway and Richard Esterle You can read about this puzzle at ludus-opuscula.org. You may notice the label on mine is mirror-written. That's intentional - I bought a rarer version. Purchased at NYPP 2016. Make a set of small 4-ball tetrahedrons, then assemble them into a large tetrahedron such that like colored balls do not touch. |

Icosa - issued by Brainwright Several challenges, including to twist the balls so that none of the same color touch, or to twist them so that there are all groups of three like-colored balls touching in triangles. Thanks, Alison! |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

Spot Cube - Hikimi Designed by Ichiro Sengoku, this puzzle was entered in the 2004 IPP Design Competition. I bought it at Torito.
|

Vier Farben Block (Four Color Block) - designed by Theo Geerinck and produced by Logika exchanged by Theo at IPP25 Helsinki Build a cube with the 12 u-shaped pieces such that like colored pieces do not touch. Each piece is one of four colors. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

Instant Indecision marked "Patent Pending" - the Green Gate Co. Sherman Oaks CA, 1972 Four cubic frames and a stepped pedestal. Each cubic frame contains twelve bars, 3 each of four overall different colors, arranged in various patterns. The four cubes are of graduated sizes and nest on the pedestal. The objective is to arrange the cubes in nested form on the pedestal so that each of the twelve sets of four aligned bars, one from each cube, contains one of each of the four colors. My version has a nice key-like tab that locks into the pedestal and holds the cubes in place for storage/transport. |

Cube Edu - eLogIQ Build a 2x2x2 cube and match colors on all faces. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

miQube - Mindware Copyright 1993-2006 IQideas, New Zealand - designed by Andrew Baker Discontinued by Mindware, but available direct from IQideas. Four multi-player games and a solitaire puzzle - assemble the 13 unique pieces (each is a four or five-unit polycube) into a 4x4x4 cube such that every side is a single (different) color. Here is a review at Boardgamegeek. The puzzle solution is available at IQideas. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

Octamania Arrange the 8 cubes into a 2x2x2 cube such that each face shows four copies of a digit. |

The vintage 8 Blocks to Madness puzzle - invented by Eric Cross of Ireland, and issued by Austin Enterprises of Ohio. Create a 2x2x2 cube having a single color on each side. Then create a 2x2x2 with each of four colors on every side. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
The Maze Cube - stack the four bricks together to make a 2x2x2 having four colors on each face. |

Poker Cubes I don't have any documentation with this puzzle, so I don't know the provenance or goal. However, I suspect the goal is to create a 2x2x2 having one of each of the four suit symbols on every side, while also ensuring each 2x2 face is a single color with each face a different color. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

The Ten Spot Domino Puzzle Issued by Valentine & Sons, Ltd. Westfield Works Dundee The instructions inside the box top read, "Valentine's Series of Popular Puzzles The New 10 Spot Domino Puzzle Instructions - Arrange the four pieces so that they form a solid square block, every side of which shows 10 spots. Solution sent on receipt of 1d. stamp." Discussed by Slocum & Botermans in their 1994 book The Book of Ingenious & Diabolical Puzzles, on page 34. The layout of the pieces and one solution are provided on page 143. Analyzed by Len Gordon and found to have seven solutions. Len also found that the pieces could be arranged to show 11 on all faces in two ways. |
I finally found a Cover Up - issued by Ideal in 1982, it originally appeared as
Hepta in 1974 and was designed by the famous Alex Randolph.
See the
entry for Hepta at Boardgamegeek.
I had wanted to try this puzzle since reading about it at
Celia Seide's website.
Celia also pointed out
Spielarchiv.de which has a reference to a version called Magic 7 under Spiele->nach Autoren->R->Randolph,Alex -> Magic 7.
There are seven plastic 1x3 straight pieces and seven angle pieces. The plastic 7x7 board is colored using 7 colors each of which appears 7 times. For each of the 7 colors, use all the pieces to cover all the spots not of the target color. It's pretty large - I put a quarter coin on the cover. 



|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

Cubic Mania Puzzle Blocks was issued by Dale Seymour Publications. It comprises eight cubes, each colored with four colors. Each cube uses each color at least once. Using the chart of cube graphs I developed, the included cubes can be mapped to the tan set { 24 x 3, 27, 34, 42, 43 x 2 }. There are several challenges, including building a 2x2x2 where every side shows all four colors, and another where every side is a solid color. |

Brain Wave Arrange the bi-colored pieces in the slots so that no color is repeated along any line of the triangle on both sides of the head. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 Lucky 13, Edition No. 7, by Fireside Games Inc. of Northbrook Illinois, 1973.
Lucky 13, Edition No. 7, by Fireside Games Inc. of Northbrook Illinois, 1973.
Comes with 38 translucent plastic pieces, each being one of 5 colors and 13 different shapes composed of unit squares joined by sides (square polyominoes) - each shape has a letter ID. The table below gives the shapes, grouped by color. The color cell gives x @ y, the count x of each piece type and the number y of unit squares the piece occupies.
Always use 3 x A, 3 x B, and 3 x F. For the remaining four pieces, pick a puzzle number from 1 through 24 and find it in the chart below. Each row and column is labeled with a piece ID. Use two copies of the piece identified by the row in which the puzzle number appears, and two copies of the piece identified by the column in which the puzzle number appears.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 Percy Alexander MacMahon
was a mathematician who lived from 1854 to 1929.
He is noted for, among other accomplishments, his results in the field of combinatorics.
In 1915 and 1916 MacMahon produced a two-volume treatise on Combinatory Analysis which
remains a respected work today.
MacMahon also produced New Mathematical Pastimes, published in 1921.
This work discusses his Colored Cubes, first introduced in a lecture he gave in 1893 [4].
If each of the n faces of a regular solid is colored with one of n colors,
the number of different ways the solid
can be colored with all n colors excluding rotations but including reflections
is given by n!/(2*E) where E is the number of edges of the solid.
For cubes with 6 faces and 12 edges, the number of possible colorings is 6!/(2*12) = 720/24 = 30.
These 30 cubes form the set of MacMahon Colored Cubes.
You can choose any of the 30 cubes to use as a "prototype" and it will be possible to
find eight other cubes in the set which can be used to build a 2x2x2 model of the prototype having the
same arrangement of solid colors on the six external 2x2 faces as on the prototype's six faces, and
also satisfying the additional constraint that internal touching faces are colored alike.
MacMahon credited his friend Colonel Julian R. Jocelyn with the discovery that this can always be done
regardless of which of the 30 cubes is chosen as the prototype.
For each prototype, there is only one set of eight cubes which will work, and there will always be two ways to
build the prototype with these eight cubes.
A procedure to transform one solution into the other was devised by L. Vosburgh Lyons and is shown in
[2] on page 190.
The eight cubes to be selected will not possess any of the same pairs of opposing face colors as the prototype.
This means that 13 of the 29 cubes can be eliminated as candidates, leaving 16 from which to choose.
Lyons also discovered that after a 1st prototype is selected along with the eight cubes to model it,
it is always possible to select another prototype from the remaining 21 cubes, and
find another 8 cubes from the remaining 20 to model this 2nd prototype.
The 2nd prototype must be a mirror image of the 1st, and the eight cubes to model it are the eight not chosen from
the 16 eligible for the modeling of the 1st prototype [2].
MacMahon sold an eight-cube puzzle patented in 1892
(UK 8275?)
to the London company R. Journet,
which marketed it as the Mayblox puzzle [4].
Its eight cubes are one of the sets which can model a prototype and meet the internal color-matching constraint.
However, the Mayblox puzzle does not specify the configuration of the prototype - so it must be deduced, which
makes the puzzle more difficult.
I made my own version of a Mayblox puzzle using LiveCube.
I chose a prototype arrangement of six colors at random, then colored the
8 sub-cubes as required based on the solution instructions in [1].
I finally found a good use for the LiveCube face plates!
Fortunately, they provide enough different colors with the addition of cyan and
pink to their previously available
black, red, yellow, green, and blue.
Percy Alexander MacMahon
was a mathematician who lived from 1854 to 1929.
He is noted for, among other accomplishments, his results in the field of combinatorics.
In 1915 and 1916 MacMahon produced a two-volume treatise on Combinatory Analysis which
remains a respected work today.
MacMahon also produced New Mathematical Pastimes, published in 1921.
This work discusses his Colored Cubes, first introduced in a lecture he gave in 1893 [4].
If each of the n faces of a regular solid is colored with one of n colors,
the number of different ways the solid
can be colored with all n colors excluding rotations but including reflections
is given by n!/(2*E) where E is the number of edges of the solid.
For cubes with 6 faces and 12 edges, the number of possible colorings is 6!/(2*12) = 720/24 = 30.
These 30 cubes form the set of MacMahon Colored Cubes.
You can choose any of the 30 cubes to use as a "prototype" and it will be possible to
find eight other cubes in the set which can be used to build a 2x2x2 model of the prototype having the
same arrangement of solid colors on the six external 2x2 faces as on the prototype's six faces, and
also satisfying the additional constraint that internal touching faces are colored alike.
MacMahon credited his friend Colonel Julian R. Jocelyn with the discovery that this can always be done
regardless of which of the 30 cubes is chosen as the prototype.
For each prototype, there is only one set of eight cubes which will work, and there will always be two ways to
build the prototype with these eight cubes.
A procedure to transform one solution into the other was devised by L. Vosburgh Lyons and is shown in
[2] on page 190.
The eight cubes to be selected will not possess any of the same pairs of opposing face colors as the prototype.
This means that 13 of the 29 cubes can be eliminated as candidates, leaving 16 from which to choose.
Lyons also discovered that after a 1st prototype is selected along with the eight cubes to model it,
it is always possible to select another prototype from the remaining 21 cubes, and
find another 8 cubes from the remaining 20 to model this 2nd prototype.
The 2nd prototype must be a mirror image of the 1st, and the eight cubes to model it are the eight not chosen from
the 16 eligible for the modeling of the 1st prototype [2].
MacMahon sold an eight-cube puzzle patented in 1892
(UK 8275?)
to the London company R. Journet,
which marketed it as the Mayblox puzzle [4].
Its eight cubes are one of the sets which can model a prototype and meet the internal color-matching constraint.
However, the Mayblox puzzle does not specify the configuration of the prototype - so it must be deduced, which
makes the puzzle more difficult.
I made my own version of a Mayblox puzzle using LiveCube.
I chose a prototype arrangement of six colors at random, then colored the
8 sub-cubes as required based on the solution instructions in [1].
I finally found a good use for the LiveCube face plates!
Fortunately, they provide enough different colors with the addition of cyan and
pink to their previously available
black, red, yellow, green, and blue.



 Odd Man Out is a version of the Mayblox puzzle, produced in wood using numbers rather than colors, by Dave Janelle at Creative Crafthouse.
You are to build a 2x2x2 cube using 8 of the 9
included numbered dice, so that every
face displays a unique number.
Odd Man Out is a version of the Mayblox puzzle, produced in wood using numbers rather than colors, by Dave Janelle at Creative Crafthouse.
You are to build a 2x2x2 cube using 8 of the 9
included numbered dice, so that every
face displays a unique number.
There have been several issues of sets of "pattern blocks" under various names.

Pattern Pending designed by Fred Horowitz and issued by Parker Brothers (General Mills) in 1971. A set of 12 black and white cubes. Fred had the basic idea for these in the 50's, and intended these to be more of an open-ended creative playset than a puzzle. |

K-Dron - Janusz Kapustra (I don't have this.) |

Trac 4 game issued in 1976 by Lakeside. Red-and-white blocks and cards specifying various patterns to construct. (Sadly, this got lost in the mail and I never received it.) |


Quiet Cubes (I don't have these.) Also designed by Fred Horowitz, a set of 18 cubes, issued in Holland. |

Rebus A set of nine patterned blocks, issued by the German company "Pussy." Create various silhouettes. |

Magritte Cube |

Tedco Mirage Numbers Up |

At Games People Play, I found a Magic Mirror puzzle from Schmidt Spiele. |


Escher Blocks from RecentToys, purchased from Bits & Pieces. |

Puzzling Reflections Ivan Moscovich 1990 Tarquin Publications |

The Mirror Puzzle Book Marion Walter Tarquin 1986 ISBN 0906212391 |

Splitting Image - from Fatbrain. Only 30 challenges. Intended for kids - very easy. |

You and Einstein Mirrorkal Invented by Ivan Moscovich Produced 2010 Recent Toys USA |

You and Mona Lisa Mirrorkal Invented by Ivan Moscovich Produced 2011 Recent Toys USA |

This is the "Fool's Spool" (made in Hong Kong). "Mix up the four wheels - rearrange them so that all lines total twelve!" One of my kids found the following solution in minutes: 5115, 1254, 5223, 4341, 2334, 3513, 4422, 3333. |



Here are more puzzles with a math theme. One is "Digi-Disc" - arrange the discs so that all equations are true. The discs adhere via magnets and I also show this puzzle in the Magnetic category. Another, from Asia, is a similar stack of discs with the same goal, but it is not magnetic. Yet another is an elongated stack, non-magnetic, called "Magic Numbers." |

Sudoku 3D Ball - 22 Advance www.3d-jp.com There are 5 circular indents on each pentagonal face of the spherical dodecahedron, and 10 indents in a "ring" bordering each face. Each indent is a member of 2 "rings" - those around the two faces adjacent to the vertex where the indent is located. Some indents already contain a digit from 0 through 9. Fill in empty indents with digits from 0 through 9 such that every ring contains all 10 digits. (The sphere is not meant to be disassembled.) |
||
|
||||

A Washington Monument "sums" puzzle, from Lambert Bright. Thanks! |

Kenken 4 - in maple, from the kind folks Adele and Peter Plantec at Puzzle Me Please. Arrange 1x1x2 blocks in the frame to form a 4x4x4 cube such that a valid KenKen 4 appears on each face. The blocks only have figures on the outside. |

Kenken 6 - in maple, from PuzzleMePlease.com Arrange 27 cubelets in the frame to form a 3x3x3 (6x6x6) cube such that a valid KenKen 6 appears on each face. The cubelets only have figures on the outside - the central cubelet has none. So, all figured faces will be used in the solution. |
||

The Enigma puzzle is a representative of this type, but with letters rather than numbers on the wheels. Form words. |

This is the Daily Mail Crossword Disc puzzle by Chad Valley. |

Daily Mirror Double Words |
||

There are several "Slivers" puzzles - this is the Anakin Skywalker version. |

Zen Blocks |

Cubits |
||

That-A-Way by Binary Arts. Introduced at IPP 20 by its creator Greg Dye. There are 10 cards/tiles each with two arrows in various orientations, and a booklet of problems and solutions. Play That-A-Way on-line. |

Flower Finder - William Waite Arrange the six pieces in the tray so that every flower has six petals. Also solve so that every flower has three petals. |

Rubik's Dice flop interior plates around until all pips show red. |
||




Binary Arts, now Thinkfun, has supplied many puzzles, including their various "something by something" puzzle/games: Brick by Brick, Square by Square, Block by Block, and Shape by Shape. |
||||

Dice Stacker by Elverson Eight wooden dice, each with a unique arrangement of spots - form a cube having four of a kind (one through six) on each side. Also, form a cube such that diagonals on each side add to seven. |

Chainbox 1981 Yonezawa - made in Japan Purchased at IPP28 A case containing four identical "chains" each made of eight black plastic links. Some of the links have orange shapes on them, front or rear. Includes a booklet of patterns to be made in the tray, using the four chains folded and arranged in different ways. |


Pakostar Purchased during IPP28 in Prague |
||


Ubongo Purchased in Berlin on the way to IPP28 in Prague. Really a game for 2-4 players, but can be played solitaire. Given a set of pieces and a deck of cards showing shapes made from those pieces, take a card and try to arrange the pieces to match the silhouette. |

Identica-L episode II Concept by Tadao Kitazawa, 2008. Purchased from Torito. Four pieces, each of which has a pattern of light and dark squares on each side. Arrange the four pieces so that the light squares form a connected shape, and the dark squares form the same shape simultaneously. The pieces can be flipped. See analysis at Ishino's site. |
|||

Hinomaru by Pavel Curtis Build the Japanese flag in the tray, using the 12 two-sided domino pieces. |


Anansi's Maze by Pavel Curtis. Purchased at IPP 29 in SF. Also available via Pavel's website. A multi-stage challenge. |

The Blockword Crosspuzzle from "Products of the Behavioral Sciences" ca. 1970 |
||

Gamesters of Triskelion, a multi-stage challenge by Pavel Curtis. |

Tiger and Panther - designed by Takahisa Nakanishi - IPP30 There are four T-tetromino and four P-pentomino pieces, each checkered. Pack them in the 6x6 tray to make stripes, and then to make a checkerboard. |

Figure Puzzle - designed by Hide Ue presented at IPP30 by Naoyuki Iwase (Osho) Seven pieces, colored light and dark variously on both sides. Arrange the pieces in the tray to form each digit 0-9 in turn. |
||

Twins - designed, made, and exchanged at IPP35 by Gary Foshee Assemble the three pieces so that each light or dark cube touches a like colored cube on at least one face, and the light and dark shapes are identical (mirror images OK). |

Cubemaker - designed by Volker Latussek, made by Pelikan Arrange the five pieces so that you form five dark cubes. Exchange puzzle of Marty Reis, entered in the 2017 Design Competition Didn't win anything, but I like this one. |

Irresistable - designed and made by Jürgen Reiche, issued at IPP35 in Ottawa. Assemble the pieces so that the two halves display identical patterns. |
||

Tridio Twist! by FatBrain Toy Co. Three mutable pieces and 48 pattern challenges. Designed by Marijn van Herel and Eliane Scharten. |

Designer Colin James very kindly sent me a copy of his Qboid puzzle. It offers over 1000 challenges at four different levels. 12 cubes, with patterned faces. When properly arranged, the patterns form digits and letters. Entered in the 2009 IPP Design Competition. Thanks, Colin! |

Royal Flush Arrange the seven L trominoes and 2 dominoes in a 5x5 grid such that every row, column, and both main diagonals contain a Royal Flush (in spades). Thanks, Dave! |
||

Dewey's Dilemma From Dave Janelle at Creative CraftHouse. Arrange 12 consecutively numbered "books" - each being one of three heights, and by one of three authors - on the included "bookshelf" such that no adjacent books are the same height, or by the same author, or consecutively numbered. |

PrimEvil, designed and made by Louis Toorenburg, exchanged at IPP32 by Paul Dudding |

Liberty Cubes, designed and exchanged at IPP32 by Kate Jones, made by Kadon Enterprises Inc. |
||

Double D Insanity, designed, made, and exchanged at IPP32 by Louis Toorenburg |

The Bricklayer's Challenge, purchased at IPP32 from Pavel Curtis |

Nats Win! aka the Baseball Scoreboard puzzle, originally designed in 1938 by the Atlantic Refining Company, publishers of the "Atlantic Baseball Book" of 1938, a giveaway. This version made by Creative Crafthouse and exchanged at IPP32 in Washington DC in 2012 by Michael Tanoff. |
||
 Bendit - from
Smart Games.
Bendit - from
Smart Games.
Designed by Raf Peeters. I purchased this at a Barnes & Noble store near me. Six different pieces, each having a sequence of black and white segments and hinged in two places. Based on a booklet of 60 challenges, fold and place the pieces in the 6x6 tray to compose a target pattern. |



Ji-Ga-Zo - website - issued by Tenyo in Japan and Hasbro in the US. Designed by puzzle-friend and magician Mark Setteducati. Kind of a color-by-number set. 300 pieces, in various shades of a color. Use supplied software to input an image and receive instructions on how best to arrange the pieces to produce the image. Similar to the art of Ken Knowlton. |

J Puzzle, designed and exchanged at IPP32 by Tsugumitsu Noji, made by ASUNARO Four pieces, three challenges: make a symmetric shape from 3 pieces; make four holes with an arrow pointing at each hole; make outlines of two pentominoes. |
||


Noah's Ark - designed by Raf Peeters, issued by Smart Games My daughter's favorite. Place the pairs of animal pieces in the ark, ensuring that the animals are upright and mates touch. Each challenge specifies the required position of one or more pieces. |
||||
|
||||


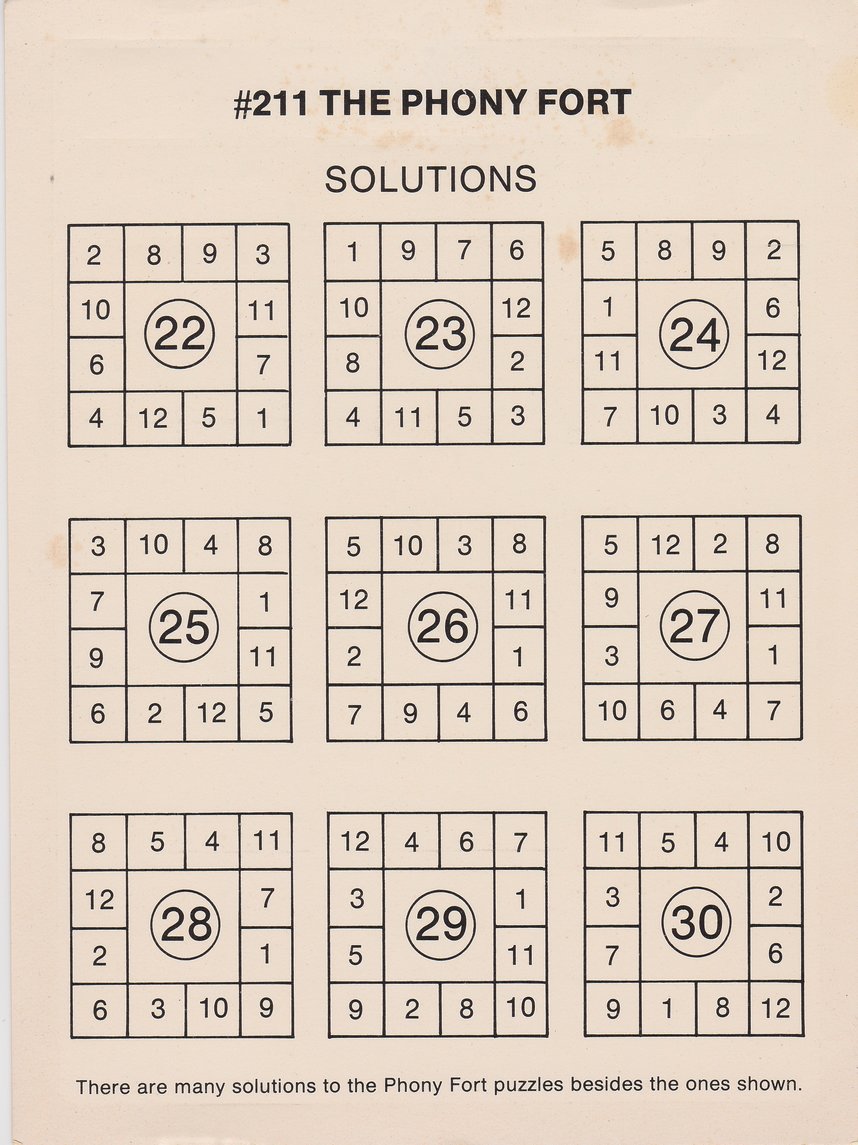
The Phony Fort - 1975 Peterson Games a number arrangement puzzle |
||||



Dinosaurs Mystic Islands - SmartGames Arrange the six 1x2 rectangular pieces in the 3x4 grid such that the red and green dinosaurs are on separate islands. Graduated challenges, becoming surprisingly difficult. A favorite! |
||||



International Puzzle Party Airports - designed by Juozas Granskas Sadly, Juozas explained to me how, try as he might, he could not fit in our IPP35 Ottawa airport YOW. Very disappointed, Jouzas! But still a fun puzzle :-) Thank you! |
||||