Rob's Puzzle Page - Interlocking Puzzles

This section covers interlocking puzzles - wherein multiple pieces fit together such that the puzzle does not fall apart and presents a challenge to disassemble and re-assemble. Use the links in the panel below to jump to a section of interest.

Happy Cubes/Snafooz (Foam Assemblies)
Cube-and-Plank (or Plate) Assemblies
Polyhedral Assemblies

Pinned Assemblies
Irregular Assemblies

The Puzzle Sculptures of Miguel Berrocal

Traditional 6-Piece Burrs

Any story about interlocking puzzles has to start with the traditional six-piece burr puzzle. This puzzle is known by several names, including the "puzzle knot," the "Devil's Knot" ( Teufelsknoten in German), the "Chinese Cross," the "Lock of Luban" (Luban Suo 魯班鎖) or the "Lock of Kongming" (Kongming Suo 孔明鎖). The term "burr" is thought to have been first used by Edwin Wyatt in Puzzles in Wood (1928), but Wyatt seems to use the term as if it was already commonly understood to apply. Supposedly whoever coined the term did so because the puzzle resembles the clinging burrs of some plants.

Like other well-known vintage puzzles, the burr has acquired a probably-fanciful backstory, and details of its history are lost. Some say it is a Chinese invention, along with the Patience Tanglement, the Sliding Piece Puzzle known as "The Huarong Path," and the Tangram, and date it to ancient times (see Wei Zhang's Chinese Puzzles Blog and chinesepuzzles.org).

According to the literature, the earliest relevant U.S. Patent seems to be 1225760 - filed by O. W. Brown on June 27, 1916 and granted on May 15, 1917. But take a look at U.S. Patent 1261242 , filed by J. W. Keiser on March 16, 1915, and granted on April 2, 1918. Keiser seems to have filed earlier but his patent was granted later. (Keiser's pieces are the Chinese Cross set; those pieces are shown in an 1857 book so Keiser did not invent them.)

A traditional six-piece burr appears in Hoffmann's 1893 book Puzzles Old and New in Chapter III as No. XXXVI "The Nut (or Six-piece) Puzzle." Another six-piece burr is shown in the 1889 Chinese book Chinese and Western Magic With Diagrams: Compilation of Magic by Tang Yunzhou. His pieces seem to be { 1, 208, 256, 670, 1024x2 } though the diagrams are a bit hard to follow. Jerry Slocum and Dieter Gebhardt put together a compendium of puzzle advertisements found in the 1785 catalogue of the merchant Peter Friedrich Catel, who established a retail store in Berlin in 1780. The 1785 catalogue contains an ad for a traditional six-piece burr puzzle called "The Small Devil's Hoof" (in addition to an ad for the Large Devil's Hoof which is a 24-piece cage burr), but the individual pieces are not shown.

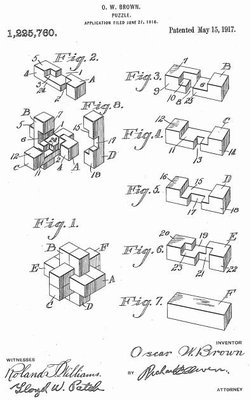
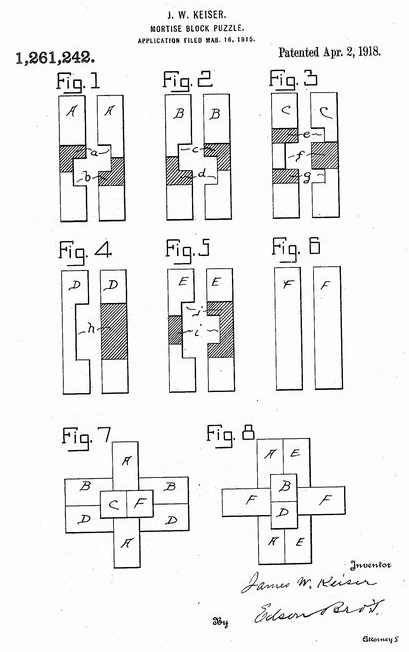
Brown's 1917 Patent filed June 1916	Keiser's 1918 Patent filed March 1915
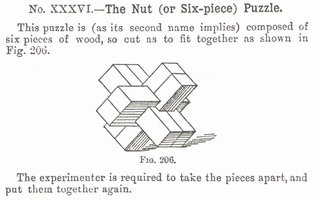
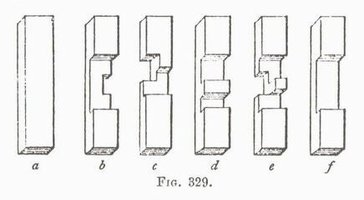
		Hoffmann's "Nut" Puzzle (1893)

One early depiction of the six-piece burr puzzle and specific pieces occurs in a Spanish book, primarily on the topic of magic, by the many-talented Pablo Minguet y Irol (b. 1700 d. ca. 1775) with a rather lengthy title that begins Enga�os � Ojos Vistas, which translates as "Deceptions in Plain Sight." (The text says the two other pieces are the solid key, and a copy of the piece labeled 3 in the diagram.)

As of Jan 2024, I am informed by Tyler Anderson that Pablo's 1733 edition does not include the pictured burr puzzle, but that it appeared in the 1755 edition. Anderson says the book was still being updated and expanded at least until 1822. Here are references:

1733 version, no burr puzzle: archive.org - 1733
1755 version, with puzzle on pages 58-59 in book / digital 78-79: archive.org - 1755
1822 version (book pp 122-3): archive.org - 1822

Minguet y Irol's Burr (1755)

Ephraim Chambers Cyclopedia frontispiece by John Sturt

In his 2007 book Geometric Puzzle Design, Stewart Coffin discusses the six-piece burr in chapter 7, and reports that Jerry Slocum's New Findings on the History of the Six Piece Burr traces the six-piece burr back to Germany in 1698. See the 1728 Cyclopedia of Ephraim Chambers (online at the University of Wisconsin Digital Collection; additional commentary at www.cyclopedia.org).

You can see a six-piece burr in the lower left area of the frontispiece by John Sturt (above on the left), which is a modified and left-to-right inverted copy of a 1698 engraving entitled "L'Acad�mie des Sciences et des Beaux Arts" by S�bastien Leclerc (or Le Clerc) (above on the right, detail at left).

Read about this engraving at the University of Oxford. It is also noted in David Singmaster's Sources in Recreational Mathematics.

Leclerc Burr 1698

Stewart Coffin's book The Puzzling World of Polyhedral Dissections hosted on John Rausch's site contains a good introduction to this type of puzzle. Martin Gardner discusses burrs briefly (as an introduction to the puzzle sculptures of Miguel Berrocal) in his 1989 book Penrose Tiles to Trapdoor Ciphers, and most of the key puzzle authors mention the puzzle. There have been sporadic fits of research into the six-piece burr, including an extensive analysis by hand by the Dutch mathematician J. H. de Boer, and work by Tom O'Beirne and Arthur Cross, but William (Bill) Cutler has performed (starting in 1975) the definitive computer analysis, and the statistics cited below are based on his analysis.

The Traditional Six-Piece Interlocking Burr Puzzle Shape

One can visualize an individual burr piece as being composed of unit cubes arranged in a 2 x 2 x 2n prism where n is greater than or equal to (and usually) 3. A solid piece will contain 24 unit cubes, and other piece types will have some of the cubes removed, resulting in notches. See diagram above left.

The burrs in this section are composed of six such pieces, often but not always distinct, selected from the overall set of possible such pieces (of a given length), and interlocked in a characteristic 2x2x2 pattern along 3 orthogonal axes. The burr shape is tricky to envision without an example in front of one, but it gets easier with practice. See diagram above right.

The Burr Shape, layer by layer

In the burr shape there are 32 internal cube positions where the pieces would overlap, but musn't in order to fit together. See above layer-by-layer diagram of an assembled burr - the internal cubies have dotted borders. These 32 internal cubes must be distributed among the six pieces in some way that (a) permits every piece to remain undivided, (b) permits the six pieces to interlock together, and (c) permits the pieces to be assembled and disassembled - i.e. it is constructible (some groups of pieces can be fit together without overlap internally, but they interlock in such a way that they could never actually be put together from scratch that way - these are called "apparent" or "false" assemblies). These constraints mean that all six pieces to be combined in a single burr puzzle, except a maximum of one possible "key" piece, must be notched to remove some cubes, and that only certain sets of notchings will work together.

One may only remove up to 10 of 12 specific cubes from a 2x2x6 prism before it becomes disjoint or improperly notched for this type of puzzle (for example, showing notches on the outside where they shouldn't be visible). Overall, this results in 837 distinct physical pieces. Cutler determined that there are 35,657,131,235 ways that six pieces drawn from the universe of 837 fit together in the requisite shape (allowing dups of pieces within a set, but discarding rotations and mirror image assemblies of sets), but of those 35 billion, "only" about 5.95 billion (estimated) are constructible puzzles.

There is a distinction made between burr puzzles that contain no internal "holes" or voids - termed solid burrs, and those that do contain one or more - termed holey burrs. There are 119,979 solid burrs, and there are 369 piece types needed to produce them. Of those 369, 112 are used in duplicate and 2 in triplicate, making a useful set of 485 pieces to make all the solid burrs. The rest of those 5.95 billion puzzles are holey burrs. A holey burr can contain from 1 to 20 holes. The weight of a burr relates to the number of internal holes it has, and can range from 32 (no internal holes), down to 12 (the maximum of 20 holes). The weight of a piece refers to the number of cubies not removed from it, and can range from 12 (the key) down to 2 (the Y). If the sum of the weights of six pieces exceeds 32, it is impossible to construct a valid burr from that set.

Also, there is a distinction made among the pieces which can be produced without hard-to-manufacture blind (or internal) corners (i.e. where the sides of at least 3 cubies meet in concavity) versus those that cannot. Any piece without any such blind corner can be made using a milling machine and is millable, otherwise it is a general type piece. (In a millable piece, any cut parallel to the long axis of the piece is bounded on both ends by a cut perpendicular to the long axis.) There are 78 millable pieces. However, to produce pieces on a table saw (with a dado blade), or by hand without resorting to a chisel, one must also avoid internal edges that run parallel to the piece's long axis, and employ only cuts running perpendicular to the long axis. These pieces are called notchable, and there are only 59 of them (they're all millable, too). Only 25 of those 59 pieces are useful to build solid burrs, and only 314 solid burrs can be made from that set of 25 (some dups are required, so you need a set of 42 pieces with dups). Overall, the 59 notchable pieces can be used to make 13,354,991 assemblies.

The level of a burr puzzle is the number of distinct linear moves (a shift of one or more pieces together, sometimes by one unit but usually by an arbitrary number of units, in just one direction) that must be performed to remove the first piece or pieces - there can be a concatenation of figures usually separated by dots - these are the numbers of steps to remove successive pieces. All solid burrs are level 1 - they come apart without any preliminary shifting. Burrs with internal holes can achieve higher levels, and one goal of research has been to delimit what is possible in terms of level complexity.

Bill Cutler has done extensive analysis on both the "holey" six-piece burr and all six-piece burrs in general, and Bill offers several burrs for sale.

Ed Pegg wrote a good survey article about burrs. Peter Roesler's site also discusses burr puzzles, and has an interesting history of Willem van der Poel's Grandfather 6x6x6 burr. You can see some burrs at John Rausch's Puzzleworld. Bruno Curfs' site (now defunct?) offered additional analysis. You can use Andreas Röver's Burr Tools to model, solve, and design burr puzzles.

Jürg von Känel created the wonderful Burr Puzzles Site that was hosted at IBM Research but now sadly seems defunct. Jürg's site offered a solution analyzer applet and historical info about burrs. In lieu of the applet, you can use BurrTools to analyze burr puzzles.

If you're interested in collecting 6-piece burrs, I suggest you first check out Ishino's "Puzzle Will Be Played" site to get some idea of the variety available. Look under "Interlocking (6 piece burr: traditional)." Though they may be sold under different names and by different vendors, burr puzzles that use the same set of six pieces are isomorphic and have identical solutions (although using pieces longer than six units might eliminate some solutions). That site also provides a comprehensive catalogue of burr pieces.

Note that when discussing traditional burrs, twists or rotations of pieces typically are not required or allowed. It is possible, however, to design burrs that appear traditional but require such moves and frustrate the usual computer analysis - for example, see Bill Cutler's Programmer's Nightmare burr. For some burr designs, twisting a piece might be possible and might offer a shortcut, but isn't strictly required. It is also possible to mimic the outer appearance of a traditional burr but use different internal notchings - but such designs are outside the scope of this section (e.g. Cutler's Explode-A-Burr).

See U.S. Patent 5040797 - Dykstra 1991 for an interesting burr that can be assembled in two distinct ways.

I admit that, early on, I didn't like burr puzzles. But as I read more about them, and tried various designs, my appreciation for them grew.
I put together the diagram below to try to summarize and organize some of the facts I learned about this category of puzzle.

Burr Analysis

Check out a nice writeup on how to go about solving 6-piece burrs, written by Guillaume Largounez, over at the Puzzle Place Wiki.

Identifying Burr Pieces

Over the years, different researchers and writers have employed different schemes to identify the pieces. Some have used rather arbitrary letters or numbers; others have devised more systematic schemes employing a mathematical calculation based on assignments of binary values to "cubies" (or "cubelets") to be removed from the unnotched basic block. I use Jürg von Känel's numbering system and I have adopted Jürg's ASCII character piece diagrams. To map my ID to Ishino's scheme, subtract 1 from my ID. For symmetric pieces without a mirror image, this gives Ishino's ID. For pieces that have a mirror image, the result gives Ishino's ID for the mirror image piece.

My piece ID is 1 plus the value, shown below, of each cubie removed.
The cubies behind cubies 256 and 512 can be removed, too, and have respective
values 1024 and 2048. Such pieces appear infrequently.

    +----+----+----+----+----+----+
   /    / 16 / 32 / 64 / 128/    /|
  +    +----+----+----+----+    + |
 /    /  1 /  2 /  4 /  8 /    /  +
+----+----+----+----+----+----+   |
|    |    |    |    |    |    |   |
|    |    |    |    |    |    |   +
+    +----+----+----+----+    +  / 
|         |    |    |         | +  
|      a  | 256| 512|  b      |/   
+----+----+----+----+----+----+

When trying to identify an arbitrary piece, rotate it about its long axis
(and maybe flip it end-for-end) until you find an orientation where
the cubies marked 'a' and 'b' and the cubies behind them are present.
Sometimes a piece could be assigned more than one number - use the smaller
number. This entails orienting it so that cubies 1024 and 2048 are present if possible.

I created a "Burr ID Tool" in JavaScript which will display an ASCII character picture of any given burr - you just check off the particular cubies that are present in the piece. (The ASCII character-based renderings rely on fixed-width fonts and won't display well on some devices, particularly phones.)

The 25 Notchable Pieces Used in Solid Burrs

Shown below is the set of 25 notchable pieces used in solid burrs. These are depicted as length-6; for longer pieces simply extend the 2x2 solid burr equally on each end.

The first number is the piece ID as described above.
The first letter, in bold, is the "standard" letter ID for the piece, and is used in Pentangle's set.
The second letter is as assigned by Curfs and is also used in Wayne Daniel's (i.e. the Interlocking Puzzles or "IP") set.
The third letter, if present, is that assigned by Edwin Wyatt in Puzzles in Wood.
A [pn] suffix, if present, indicates the piece is included in the Professor burr set and n is the count (1 if absent).
The next number is the count of this piece in a 42-piece set that allows you to construct 314 solid burrs.
The last number is the count of this piece in the Level-5 set.

I have lately given names to some of the pieces, which I find more helpful than the letters or numbers when trying to remember sets of pieces I have seen before.

Piece #1 is the "key" piece. No more than one Key appears in any puzzle. Also, when the key #1 is used, neither #18 nor #35 can be used in the same puzzle with it. (Can you tell why?) Piece 1024 (Y) is the "minimal" piece - no more material can be removed without the piece falling apart.

I have located some of the pieces out of numerical sequence, to show related pieces together.

1 A A A [p] 1 0 +----+----+----+----+----+----+ / /\| + + \| / / + +----+----+----+----+----+----+ \| \| \| \| \| \| + + + / \| \| + \| \|/ +----+----+----+----+----+----+ The Key
All six positions and widths of a single slot...
18 B B L [p] 2 0 +----+ +----+----+----+----+ / /\| / /\| + + \| + + \| / / +-/ / + +----+ / +----+----+----+----+ \| \| \| + \| \| \| \| \|/ \| \| + + +----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ Local Mail	35 C E 1 0 +----+----+ +----+----+----+ / /\| / /\| + + \| + + \| / / +-/ / + +----+----+ / +----+----+----+ \| \| \| + \| \| \| \| \|/ \| \| + + +----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ Out of Town Mail	52 D P J [p] 2 0 +----+ +----+----+----+ / /\| / /\| + + \| + + \| / / +----+-/ / + +----+ / +----+----+----+ \| \| \| + \| \| \| \| \|/ \| \| + + +----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ The Side Tray	103 F S H 1 1 +----+----+ +----+----+ / /\| / /\| + + \| + + \| / / +---+--/ / + +----+----+ / +----+----+ \| \| \| + \| \| \| \| \|/ \| \| + + +----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ The Half-Tray	120 G U 1 1 +----+ +----+----+ / /\| / /\| + + \| + + \| / / +----+---+--/ / + +----+ / +----+----+ \| \| \| + \| \| \| \| \|/ \| \| + + +----+----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ The Three-Quarters Tray	256 J X B [p2] 3 2 +----+ +----+ / /\| / /\| + + \| + + \| / / +----+----+----+-/ / + +----+ / +----+ \| \| \| + \| \| \| \| \|/ \| \| + + +----+----+----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ The Tray
Three possible dual slots...			Three symmetric pieces...
86 E H 1 0 +----+ +----+ +----+----+ / /\| / /\| / /\| + + \| + + \| + + \| / / +-/ / +-/ / + +----+ / +----+ / +----+----+ \| \| \| + \| \| + \| \| \| \| \|/ \| \|/ \| \| + + +----+ +----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ The Mailbox	154 H K I [p] 1 1 +----+ +----+----+ +----+ / /\| / /\| / /\| + + \| + + \| + + \| / / +-/ / +-/ / + +----+ / +----+----+ / +----+ \| \| \| + \| \| + \| \| \| \| \|/ \| \|/ \| \| + + +----+ +----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ The Toaster	188 I M M [p] 2 1 +----+ +----+ +----+ / /\| / /\| / /\| + + \| + + \| + + \| / / +----+-/ / +-/ / + +----+ / +----+ / +----+ \| \| \| + \| \| + \| \| \| \| \|/ \| \|/ \| \| + + +----+----+ +----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ The (Bottle) Opener	871 M T K 2 0 +----+----+ +----+----+ / /\| / /\| + + \| + + \| / / +----+-/ / + +----+----+ / +----+----+ \| \| \| +----+--\| \| \| \| \| \| \| \| + + + \| + + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ The Barbells	928 V L D 2 1 +----+ +----+----+ +----+ / /\| / /\| / /\| + + \| +----+----+ \| + + \| / / +--\| \| +-/ / + +----+ / \| \|/ +----+ \| \| \| + + + \| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ The Tongue	1024 Y Y F [p2] 3 1 +----+ +----+ / /\| / /\| + + \| + + \| / / +----+----+----+-/ / + +----+ / +----+ \| \| \| + +----+----+ \| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ The Y
There are six pairs of mirror image pieces...
359 L F 1 0 +----+----+----+ +----+----+ / /\| / /\| + +----+ \| + + \| / /\| \| +-/ / + +----+----+ \| \|/ +----+----+ \| \| \| + +--\| \| \| \| \| \| \| \| + + + \| + + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+	615 K G 1 0 +----+----+ +----+----+----+ / /\| / /\| + + \| +----+ + \| / / +--\| / / + +----+----+ / \| +----+----+ \| \| \| +----+ \| \| \| \| \| \| \| \| + + + \| + + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+	792 R D 2 0 +----+ +----+----+----+----+ / /\| / /\| + + \| +----+----+ + \| / / +--\| / / + +----+ / \| +----+----+ \| \| \| + + \| \| \| \| \|/ /\| \| \| + + +----+ \| + + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+	911 N C G 2 0 +----+----+----+----+ +----+ / /\| / /\| + +----+----+ \| + + \| / /\| \| +-/ / + +----+----+ \| \|/ +----+ \| \| \| + + \| \| \| \| \| \| / \| \| + + + \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+	824 T R C [p] 2 1 +----+ +----+----+----+ / /\| / /\| + + \| +----+ + \| / / +----+--\| / / + +----+ / \| +----+----+ \| \| \| + +----+ \| \| \| \| \|/ /\| \| \| + + +----+ \| + + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+	975 O Q E [p] 2 1 +----+----+----+ +----+ / /\| / /\| + +----+ \| + + \| / /\| \| +----+-/ / + +----+----+ \| \|/ +----+ \| \| \| + +----+ \| \| \| \| \| \| / \| \| + + + \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+
The Notched Half-Trays		The Walls		The Offsets
856 S J 1 1 +----+ +----+ +----+----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +--\| \| +-/ / + +----+ / \| \|/ +----+----+ \| \| \| + + +--\| \| \| \| \|/ /\| \| \| + + +----+ \| + + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+	943 P I 1 1 +----+----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +--\| \| +-/ / + +----+----+ / \| \|/ +----+ \| \| \| +----+ + \| \| \| \| \| \| / \| \| + + + \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+	888 U W 2 1 +----+ +----+----+ / /\| / /\| + + \| + + \| / / +----+----+-/ / + +----+ / +----+----+ \| \| \| + +----+--\| \| \| \| \|/ /\| \| \| + + +----+ \| + + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+	1007 Q V 2 1 +----+----+ +----+ / /\| / /\| + + \| + + \| / / +----+----+-/ / + +----+----+ / +----+ \| \| \| +----+----+ \| \| \| \| \| \| / \| \| + + + \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+	960 X N 2 2 +----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +-------\| \| +-/ / + +----+ / \| \|/ +----+ \| \| \| + +----+ + \| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+	992 W O [p] 2 2 +----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +--\| \| +----+-/ / + +----+ / \| \|/ +----+ \| \| \| + + +----+ \| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+
The Fingered Clubs		The Clubs		The Fingers

Selected Other Burr Pieces

The following are only a small selection of additional pieces (or 'non-25' pieces - i.e. pieces not in the set of 25 given above), used in some of the burrs mentioned below, where they will be highlighted like this.

The pieces are in numerical order from top down left to right, but I show mirror image pairs together using an arbitrary color. Notchable pieces will have an N after the ID#, non-notchable but millable pieces will have an M. Non-millable (and therefore non-notchable) pieces have internal corners and are more difficult to manufacture. Remember, there are 837 pieces in total - if you want to see them all, you'd best visit Ishino's site - though Ishino uses a different numbering scheme.

I have added the 20 non-25 pieces from the 27-piece Ultimate Burr Set - they're labeled UBS.n where n is the piece number as given within the set.
The UBS set includes 7 of the 25 pieces above (shown as 'UBS number = my ID'):
0=1, 25=188, 9=256, 10=928, 5=1024, 7/6=960/992

I have also included the 20 non-25 pieces from the 35-piece Interlocking Puzzles Level-5 Set - they're labeled IPL5S.n x where n is the piece number as given within the set and x is the count included in the set.
The IPL5 set includes 15 of the 25 pieces above (shown as 'IPL5 number = my ID'):
46=103, 22=120, 56=154, 26=188, 00=256, 35=928, 01=1024, 30/08=824/975, 09/29=856/943, 03/02=888/1007, 28/07=960/992

20 +----+ +----+----+----+----+ / /\| / /\| + + \| +----+ + \| / / +--\| / / + +----+ / \| +----+----+----+ \| \| \| + +--\| \| \| \| \|/ \| \| + + +----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ Filipiak #67	56 +----+ +----+----+----+ / /\| / /\| + + \| +----+ + \| / / +----+--\| / / + +----+ / \| +----+----+ \| \| \| + +--\| \| \| \| \|/ \| \| + + +----+----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ Triple Slide	60 +----+ +----+----+----+ / /\| / /\| + + \| + +----+ + \| / / +----+-/ /\| / / + +----+ / +----+ \| +----+ \| \| \| + \| \| +--\| \| \| \| \|/ \| \|/ \| \| + + +----+----+ +----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ UBS.1	64 +----+ +----+----+----+ / /\| / /\| + + \| +----+----+ + \| / / +----+--\| / / + +----+ / \| +----+ \| \| \| + +----+--\| \| \| \| \|/ \| \| + + +----+----+----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ UBS.24	72 +----+----+----+ +----+----+ / /\| / /\| + +----+----+ \| + + \| / /\| \| +-/ / + +----+ \| \|/ +----+----+ \| \| \| +----+----+ \| \| \| \| \|/ \| \| + + +----+----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ Interrupted Slide	88 M +----+ +----+ +----+----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +--\| \| +-/ / + +----+ / \| \|/ +----+----+ \| \| \| + +----+ \| \| \| \| \|/ \| \| + + +----+----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ Piston, Hordern, Dozen, BB31-10-40
94 +----+ +----+ +----+----+ / /\| / /\| / /\| + + \| + + \| +----+ + \| / / +-/ / +--\| / / + +----+ / +----+ / \| +----+ \| \| \| + \| \| + +--\| \| \| \| \|/ \| \|/ \| \| + + +----+ +----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ Triple Slide	109 +----+----+ +----+----+ / /\| / /\| + +----+ +----+ + \| / /\|----\| / / + +----+----+----+ \| \| +----+ \| \| \| + +--\| \| \| \| \|/ \| \| + + +----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ BCL6000	112 +----+----+ +----+----+ / /\| / /\| + +----+ \| +----+ + \| / /\| \| +-------\| / / + +----+ \| \|/ \| +----+ \| \| \| +----+ +--\| \| \| \| \|/ \| \| + + +----+----+----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ Interrupted Slide	124 +----+ +----+----+ / /\| / /\| + + \| +----+----+ + \| / / +----+-/ /\| / / + +----+ / +----+ \| +----+ \| \| \| + \| \| +--\| \| \| \| \|/ \| \|/ \| \| + + +----+----+ +----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ UBS.22	126 +----+ +----+----+ / /\| / /\| + + \| +----+ +----+ + \| / / +-/ /\|----\| / / + +----+ / +----+ \| \| +----+ \| \| \| + \| \| + +--\| \| \| \| \|/ \| \|/ \| \| + + +----+ +----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ STC#36	216 +----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+ \| +----+ + \| / / +--\| \| +-/ / + +----+ / \| \|/ +----+----+ \| \| \| + +----+ \| \| \| \| \|/ \| \| + + +----+----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ Eight is Enough
128 +----+ +----+----+ / /\| / /\| + + \| +----+ + \| / / +------------\| / / + +----+ / \| +----+ \| \| \| + +--\| \| \| \| \|/ \| \| + + +----+----+----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ Hedgehog, Kaldeway, UBS.15	240 +----+----+ +----+ / /\| / /\| + +----+ \| + + \| / /\| \| +----+----+-/ / + +----+ \| \|/ +----+ \| \| \| +----+ \| \| \| \| \|/ \| \| + + +----+----+----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ Avenger (pc. #4)	156 +----+ +----+----+ +----+ / /\| / /\| / /\| + + \| +----+ + \| + + \| / / +--\| / / +-/ / + +----+ / \| +----+ / +----+ \| \| \| + +--\| \| + \| \| \| \| \|/ \| \|/ \| \| + + +----+----+ +----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ Triple Slide	160 M +----+ +----+----+ +----+ / /\| / /\| / /\| + + \| +----+----+ \| + + \| / / +--\| \| +-/ / + +----+ / \| \|/ +----+ \| \| \| + +----+----+ \| \| \| \| \|/ \| \| + + +----+----+----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ (many)	192 M +----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +----+--\| \| +-/ / + +----+ / \| \|/ +----+ \| \| \| + +----+ \| \| \| \| \|/ \| \| + + +----+----+----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ #G, UBS.17	224 M +----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +--\| \| +----+-/ / + +----+ / \| \|/ +----+ \| \| \| + +----+ \| \| \| \| \|/ \| \| + + +----+----+----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ JVK, Millable 5.4, UBS.14
327 N +----+----+----+ +----+----+ / /\| / /\| + +----+ \| + + \| / /\| \| +-/ / + +----+----+ \| \|/ +----+----+ \| \| \| + + \| \| \| \| \| \| / \| \| + + + \| +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ IPL5S.39 1	551 N +----+----+ +----+----+----+ / /\| / /\| + + \| +----+ + \| / / +--\| / / + +----+----+ / \| +----+----+ \| \| \| + + \| \| \| \| \|/ /\| \| \| + + +----+ \| + + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+ BC-L5N, IPL5S.45 1	344 N +----+ +----+ +----+----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +--\| \| +-/ / + +----+ / \| \|/ +----+----+ \| \| \| + + + \| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ IPL5S.25 2	687 N +----+----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +--\| \| +-/ / + +----+----+ / \| \|/ +----+ \| \| \| + + + \| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+ IPL5S.33 1	376 N +----+ +----+----+ / /\| / /\| + + \| + + \| / / +----+----+-/ / + +----+ / +----+----+ \| \| \| + +----+ \| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ IPL5S.21 1	751 N +----+----+ +----+ / /\| / /\| + + \| + + \| / / +----+----+-/ / + +----+----+ / +----+ \| \| \| + +----+ \| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+ IPL5S.05 1
410 +----+ +----+----+ +----+ / /\| / /\| / /\| + + \| + + \| + + \| / / +-/ / +-/ / + +----+ / +----+----+ / +----+ \| \| \| + \| \| + \| \| \| \| \|/ \| \|/ \| \| + + +----+----+ +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ UBS.2	412 N +----+ +----+----+ +----+ / /\| / /\| / /\| + + \| +----+ + \| + + \| / / +--\| / / +-/ / + +----+ / \| +----+ / +----+ \| \| \| + + \| \| + \| \| \| \| \|/ /\| \| \|/ \| \| + + +----+ \| + +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ (many), UBS.23, IPL5S.53 1	670 N +----+ +----+----+ +----+ / /\| / /\| / /\| + + \| + +----+ \| + + \| / / +-/ /\| \| +-/ / + +----+ / +----+ \| \|/ +----+ \| \| \| + \| \| + + \| \| \| \| \|/ \| \| \| / \| \| + + +----+ + \| +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+ IPL5S.40 1	414 +----+ +----+----+ +----+ / /\| / /\| / /\| + + \| + +----+ \| + + \| / / +-/ /\| \| +-/ / + +----+ / +----+ \| \|/ +----+ \| \| \| + \| \| +----+ \| \| \| \| \|/ \| \|/ \| \| + + +----+----+----+----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ UBS.3	416 M +----+ +----+----+ +----+ / /\| / /\| / /\| + + \| +----+----+ \| + + \| / / +--\| \| +-/ / + +----+ / \| \|/ +----+ \| \| \| + + +----+ \| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ UBS.20	442 +----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+ + \| + + \| / / +-/ / +-/ / + +----+ / +----+----+ / +----+ \| \| \| + \| \| + \| \| \| \| \|/ \| \|/ \| \| + + +----+----+ +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ UBS.4
444 N +----+ +----+ +----+ / /\| / /\| / /\| + + \| + + \| + + \| / / +----+-/ / +-/ / + +----+ / +----+ / +----+ \| \| \| + +--\| \| + \| \| \| \| \|/ /\| \| \|/ \| \| + + +----+ \| + +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ UBS.18, IPL5S.49 1	734 N +----+ +----+ +----+ / /\| / /\| / /\| + + \| + + \| + + \| / / +-/ / +----+-/ / + +----+ / +----+ / +----+ \| \| \| + \| \| +----+ \| \| \| \| \|/ \| \| \| / \| \| + + +----+ + \| +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+ IPL5S.10 1	448 M +----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +----+--\| \| +-/ / + +----+ / \| \|/ +----+ \| \| \| + +----+----+ \| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ Interrupted Slide, UBS.12	736 M +----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +--\| \| +----+-/ / + +----+ / \| \|/ +----+ \| \| \| + +----+----+ \| \| \| \| \|/ /\| / \| \| + + +----+----+ \| +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+ BCL6000, #G	463 N +----+----+----+ +----+ / /\| / /\| + +----+ \| + + \| / /\| \| +----+-/ / + +----+----+ \| \|/ +----+ \| \| \| + + \| \| \| \| \| \| / \| \| + + + \| +----+----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ Tenyo Brother, IPL5S.24 1	568 N +----+ +----+----+----+ / /\| / /\| + + \| +----+ + \| / / +----+--\| / / + +----+ / \| +----+----+ \| \| \| + + \| \| \| \| \|/ /\| \| \| + + +----+----+ \| + + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+ IPL5S.34 1
464 +----+----+----+ +----+ / /\| / /\| + +----+----+ \| + + \| / /\| \| +----+-/ / + +----+ \| \|/ +----+ \| \| \| +----+ + \| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ Brown's	576 +----+ +----+----+----+ / /\| / /\| + + \| +----+----+ + \| / / +----+--\| / / + +----+ / \| +----+ \| \| \| + + +--\| \| \| \| \|/ /\| / \| \| + + +----+----+ \| +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+ D. Kriz II	474 +----+ +----+ +----+ / /\| / /\| / /\| + + \| + +----+ + + \| / / +-/ /\|-+-/ / + +----+ / +----+----+ \| +----+ \| \| \| + \| \| + \| \| \| \| \|/ \| \|/ \| \| + + +----+----+ +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ UBS.26	476 +----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+----+ + + \| / / +--\| / /\|-+-/ / + +----+ / \| +----+ \| +----+ \| \| \| + + \| \| + \| \| \| \| \|/ /\| \| \|/ \| \| + + +----+ \| + +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ Prog. Nightmare, UBS.21	702 +----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+----+ \| + + \| / / +-/ /\| \| +-/ / + +----+ / +----+ \| \|/ +----+ \| \| \| + \| \| + + \| \| \| \| \|/ \| \| \| / \| \| + + +----+ + \| +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+ BC-CCU10, Mega-6	478 +----+ +----+ +----+ / /\| / /\| / /\| + + \| + + \| + + \| / / +-/ / +----+-/ / + +----+ / +----+ / +----+ \| \| \| + \| \| + \| \| \| \| \|/ \| \|/ \| \| + + +----+----+----+----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ UBS.16
480 N +----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +--\| \| +----+-/ / + +----+ / \| \|/ +----+ \| \| \| + + + \| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ UBS.13, IPL5S.23 3	704 N +----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +----+--\| \| +-/ / + +----+ / \| \|/ +----+ \| \| \| + + + \| \| \| \| \|/ /\| / \| \| + + +----+----+ \| +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+ (many), IPL5S.32 2	495 N +----+----+ +----+ / /\| / /\| + + \| + + \| / / +----+----+-/ / + +----+----+ / +----+ \| \| \| +----+ \| \| \| \| \| \| / \| \| + + + \| +----+----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ IPL5S.20 1	632 N +----+ +----+----+ / /\| / /\| + + \| + + \| / / +----+----+-/ / + +----+ / +----+----+ \| \| \| + +--\| \| \| \| \|/ /\| \| \| + + +----+----+ \| + + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+ IPL5S.06 1	499 +----+ +----+ / /\| / /\| + +----+ +----+----+ + \| / /\|-+-/ / + +----+----+ \| +----+----+----+ \| \| \| +--\| \| \| \| \| \| \| \| + + + \| + + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ BC-CC5H	757 +----+ +----+ / /\| / /\| + +----+----+ +----+ + \| / /\|-+-/ / + +----+----+----+ \| +----+----+ \| \| \| +--\| \| \| \| \| \| \| \| + + + \| + + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+ Prog. Nightmare
506 +----+ +----+ / /\| / /\| + + \| +----+----+ + + \| / / +-/ /\|-+-/ / + +----+ / +----+----+ \| +----+ \| \| \| + \| \| + \| \| \| \| \|/ \| \|/ \| \| + + +----+----+ +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ UBS.19	508 M +----+ +----+ / /\| / /\| + + \| +----+ + + \| / / +----+-/ /\|-+-/ / + +----+ / +----+ \| +----+ \| \| \| + +--\| \| + \| \| \| \| \|/ /\| \| \|/ \| \| + + +----+ \| + +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ UBS.11	511 +----+ +----+ / /\| / /\| + +----+ + + \| / /\|-+----+----+-/ / + +----+----+ \| +----+ \| \| \| +----+ \| \| \| \| \| \| / \| \| + + + \| +----+----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ Interrupted Slide, #D, F#73	760 +----+ +----+ / /\| / /\| + + \| +----+ + \| / / +----+----+-/ / + +----+ / +----+----+ \| \| \| + +--\| \| \| \| \|/ /\| \| \| + + +----+----+ \| + + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+ Baffling, Brother	512 N +----+ +----+ / /\| / /\| + + \| + + \| / / +----+----+----+-/ / + +----+ / +----+ \| \| \| + +----+ \| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ (many), UBS.8, IPL5S.19 1	768 N +----+ +----+ / /\| / /\| + + \| + + \| / / +----+----+----+-/ / + +----+ / +----+ \| \| \| + +----+ \| \| \| \| \|/ /\| / \| \| + + +----+----+ \| +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+ (many), IPL5S.04 1
564 +----+ +----+----+----+ / /\| / /\| + + \| + + \| / / +----+-/ / + +----+ / +----+----+----+ \| \| \| + \| \| \| \| \|/ \| \| + + +----+----+----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+ Tenyo Brother	624 +----+----+ +----+----+ / /\| / /\| + +----+ \| +----+ + \| / /\| \| +----+--\| / / + +----+ \| \|/ \| +----+ \| \| \| +----+ +----+--\| \| \| \| \|/ /\| / \| \| + + +----+----+ \| +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+ BC-CCU10	800 +----+ +----+----+----+----+ / /\| / /\| + + \| +----+----+----+ + \| / / +--\| / / + +----+ / \| +----+ \| \| \| + + +--\| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ Brown's	820 +----+ +----+----+----+ / /\| / /\| + + \| + + \| / / +----+-/ / + +----+ / +----+----+----+ \| \| \| + +--\| \| \| \| \|/ /\| \| \| + + +----+ \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ STC#36	832 +----+ +----+----+----+ / /\| / /\| + + \| +----+----+ + \| / / +----+--\| / / + +----+ / \| +----+ \| \| \| + +----+ +--\| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ Brown's, G4	976 +----+----+----+ +----+ / /\| / /\| + +----+----+ \| + + \| / /\| \| +----+-/ / + +----+ \| \|/ +----+ \| \| \| +----+ +----+ \| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ D. Kriz II, Enigma, #G
880 +----+----+ +----+----+ / /\| / /\| + +----+ \| +----+ + \| / /\| \| +----+--\| / / + +----+ \| \|/ \| +----+ \| \| \| +----+----+----+--\| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ Dubois/Gaby	883 +----+ +----+----+ / /\| / /\| + +----+ +----+ + \| / /\|-+-/ / + +----+----+ \| +----+----+----+ \| \| \| +--\| \| \| \| \| \| \| \| + + + \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ BC-CCU10	896 +----+ +----+----+ / /\| / /\| + + \| +----+ + \| / / +----+----+--\| / / + +----+ / \| +----+ \| \| \| + +----+----+--\| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ Avenger (pc. #2)	1008 +----+----+ +----+ / /\| / /\| + +----+ \| + + \| / /\| \| +----+----+-/ / + +----+ \| \|/ +----+ \| \| \| +----+----+----+ \| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ (many)	909 +----+----+----+----+ +----+ / /\| / /\| + +----+ \| + + \| / /\| \| +-/ / + +----+----+----+ \| \|/ +----+ \| \| \| + + \| \| \| \| \|/ / \| \| + + +----+ +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ Tenyo Brother	922 +----+ +----+----+ +----+ / /\| / /\| / /\| + + \| + + \| + + \| / / +-/ / +-/ / + +----+ / +----+----+ / +----+ \| \| \| + \| \| + \| \| \| \| \|/ \| \|/ \| \| + + +----+----+----+----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ Piston
926 +----+ +----+----+ +----+ / /\| / /\| / /\| + + \| + +----+ \| + + \| / / +-/ /\| \| +-/ / + +----+ / +----+ \| \|/ +----+ \| \| \| + \| \| + + \| \| \| \| \|/ \| \|/ / \| \| + + +----+----+ +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ BC-CC5H	927 +----+ +----+----+ +----+ / /\| / /\| / /\| + +----+----+----+ \| + + \| / /\| \| +-/ / + +----+----+ \| \|/ +----+ \| \| \| + + \| \| \| \| \| \| / \| \| + + + \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ Tenyo Brother	956 +----+ +----+ +----+ / /\| / /\| / /\| + + \| + + \| + + \| / / +----+-/ / +-/ / + +----+ / +----+ / +----+ \| \| \| + +--\| \| + \| \| \| \| \|/ /\| \| \|/ \| \| + + +----+ \| +----+----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ Prog. Nightmare, BC-CC4H	990 +----+ +----+ +----+ / /\| / /\| / /\| + + \| + + \| + + \| / / +-/ / +----+-/ / + +----+ / +----+ / +----+ \| \| \| + \| \| +----+ \| \| \| \| \|/ \| \|/ / \| \| + + +----+----+ +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ Interrupted Slide	984 +----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+ \| +----+ + \| / / +--\| \| +-/ / + +----+ / \| \|/ +----+----+ \| \| \| + + +--\| \| \| \| \|/ /\| \| \| + + +----+ \| + + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ Avenger (pc. #7)	996 +----+----+ +----+ / /\| / /\| + +----+ \| +----+----+ + \| / /\| \| +-/ / + +----+ \| \|/ +----+----+----+ \| \| \| +----+--\| \| \| \| \|/ /\| \| \| + + +----+ \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ Baffling
1015 +----+ +----+ / /\| / /\| + +----+ +----+ + \| / /\|-+----+-/ / + +----+----+ \| +----+----+ \| \| \| +----+--\| \| \| \| \| \| \| \| + + + \| + + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ (many)	1016 +----+ +----+ / /\| / /\| + + \| +----+ + \| / / +----+----+-/ / + +----+ / +----+----+ \| \| \| + +----+--\| \| \| \| \|/ /\| \| \| + + +----+ \| + + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ Tenyo Brother	1021 +----+ +----+ / /\| / /\| + +----+----+ + + \| / /\|-+----+-/ / + +----+----+----+ \| +----+ \| \| \| +----+ \| \| \| \| \|/ / \| \| + + +----+ +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ Prog. Nightmare	1023 +----+ +----+ / /\| / /\| + +----+ + + \| / /\|-+----+----+-/ / + +----+----+ \| +----+ \| \| \| +----+----+ \| \| \| \| \| \| / \| \| + + + \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ Teufelsknoten Schlüsselanhänger	1933 N +----+----+----+----+ +----+ / /\| / /\| + +----+ \| + + \| / /\| \| +-/ / + +----+----+----+ \| \|/ +----+ \| \| \| + + \| \| \| \| \|/\| / \| \| + + +----+ \| +----+ + / \| \| + +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ Avenger (pc. #9), IPL5S.38 1	2836 N +----+ +----+----+----+----+ / /\| / /\| + + \| +----+ + \| / / +--\| / / + +----+ / \| +----+----+----+ \| \| \| + + \| \| \| \| \|/ /\| \| \| + + +----+ \| +----+ + / \| \| +----+ \| \| + \| \|/ \| \|/ +----+----+ +----+----+ IPL5S.44 1

There are 59 notchable pieces - they include the 25 shown above used in solid burrs, and there are another 10 mirror pairs shown in the table above (marked as 'N'). Besides those 45 pieces, there are an additional 14 notchable pieces (six mirror pairs and 2 mirror symmetric pieces) that seem to appear infrequently, if at all - I call them the 14 Obscure Notchables and I show them in the table below.

276 N

    +----+    +----+----+----+----+
   /    /|   /                   /|
  +    + |  +----+              + |
 /    /  +--|   /              /  +
+----+  /   |  +----+----+----+   |
|    | +    +  |              |   |
|    |/    /|  |              |   +
+    +----+ |  +              +  / 
|         | +--|              | +  
|         |/   |              |/   
+----+----+    +----+----+----+

653 N

    +----+----+----+----+    +----+
   /                   /|   /    /|
  +              +----+ |  +    + |
 /              /|    | +-/    /  +
+----+----+----+ |    |/ +----+   |
|              | +    +  |    |   |
|              | |   /   |    |   +
+              + |  +----+    +  / 
|              | +--|         | +  
|              |/   |         |/   
+----+----+----+    +----+----+

291 N

    +----+----+    +----+----+----+
   /         /|   /              /|
  +         + |  +              + |
 /         /  +-/              /  +
+----+----+  / +----+----+----+   |
|         | +--|              |   |
|         | |  |              |   +
+         + |  +              +  / 
|         | +--|              | +  
|         |/   |              |/   
+----+----+    +----+----+----+

(291 has no mirror)

308 N

    +----+         +----+----+----+
   /    /|        /              /|
  +    + |       +              + |
 /    /  +----+-/              /  +
+----+  /      +----+----+----+   |
|    | +    +--|              |   |
|    |/    /|  |              |   +
+    +----+ |  +              +  / 
|         | +--|              | +  
|         |/   |              |/   
+----+----+    +----+----+----+

717 N

    +----+----+----+         +----+
   /              /|        /    /|
  +              + |       +    + |
 /              /  +----+-/    /  +
+----+----+----+  /      +----+   |
|              | +----+  |    |   |
|              | |   /   |    |   +
+              + |  +----+    +  / 
|              | +--|         | +  
|              |/   |         |/   
+----+----+----+    +----+----+

395 N

    +----+----+----+----+    +----+
   /                   /|   /    /|
  +         +----+    + |  +    + |
 /         /|   /    /  +-/    /  +
+----+----+ |  +----+  / +----+   |
|         | +  |    | +  |    |   |
|         | |  |    |/   |    |   +
+         + |  +    +----+    +  / 
|         | +--|              | +  
|         |/   |              |/   
+----+----+    +----+----+----+

534 N

    +----+    +----+----+----+----+
   /    /|   /                   /|
  +    + |  +    +----+         + |
 /    /  +-/    /|   /         /  +
+----+  / +----+ |  +----+----+   |
|    | +  |    | +  |         |   |
|    |/   |    | |  |         |   +
+    +----+    + |  +         +  / 
|              | +--|         | +  
|              |/   |         |/   
+----+----+----+    +----+----+

427 N

    +----+----+    +----+    +----+
   /         /|   /    /|   /    /|
  +         + |  +    + |  +    + |
 /         /  +-/    /  +-/    /  +
+----+----+  / +----+  / +----+   |
|         | +--|    | +  |    |   |
|         | |  |    |/   |    |   +
+         + |  +    +----+    +  / 
|         | +--|              | +  
|         |/   |              |/   
+----+----+    +----+----+----+

598 N

    +----+    +----+    +----+----+
   /    /|   /    /|   /         /|
  +    + |  +    + |  +         + |
 /    /  +-/    /  +-/         /  +
+----+  / +----+  / +----+----+   |
|    | +  |    | +--|         |   |
|    |/   |    | |  |         |   +
+    +----+    + |  +         +  / 
|              | +--|         | +  
|              |/   |         |/   
+----+----+----+    +----+----+

1417 N

    +----+----+----+----+    +----+
   /                   /|   /    /|
  +                   + |  +    + |
 /                   /  +-/    /  +
+----+----+----+----+  / +----+   |
|                   | +  |    |   |
|                   |/   |    |   +
+         +----+    +----+    +  / 
|         | +  |              | +  
|         |/   |              |/   
+----+----+    +----+----+----+

(1417 has no mirror)

1419 N

    +----+----+----+----+    +----+
   /                   /|   /    /|
  +         +----+    + |  +    + |
 /         /|   /    /  +-/    /  +
+----+----+ |  +----+  / +----+   |
|         | +--|    | +  |    |   |
|         |   +|    |/   |    |   +
+         +  / +    +----+    +  / 
|         | +  |              | +  
|         |/   |              |/   
+----+----+    +----+----+----+

1449 N (2582)

    +----+    +----+----+----+----+
   /    /|   /                   /|
  +    + |  +    +----+         + |
 /    /  +-/    /|   /         /  +
+----+  / +----+ |  +----+----+   |
|    | +  |    | +--|         |   |
|    |/   |    |   +|         |   +
+    +----+    +  / +         +  / 
|              | +  |         | +  
|              |/   |         |/   
+----+----+----+    +----+----+

1449 N (rotated)

    +----+----+    +----+    +----+
   /         /|   /    /|   /    /|
  +         +----+    + |  +    + |
 /                   /  +-/    /  +
+----+----+----+----+  / +----+   |
|                   | +  |    |   |
|                   |/   |    |   +
+         +----+    +----+    +  / 
|         | +  |              | +  
|         |/   |              |/   
+----+----+    +----+----+----+

1935 N

    +----+----+----+----+    +----+
   /                   /|   /    /|
  +         +----+----+ |  +    + |
 /         /|         | +-/    /  +
+----+----+ |         |/ +----+   |
|         | +----+    +  |    |   |
|         |   +  |   /   |    |   +
+         +  /   |  +----+    +  / 
|         | +    +--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

2840 N

    +----+    +----+----+----+----+
   /    /|   /                   /|
  +    + |  +----+----+         + |
 /    /  +--|        /         /  +
+----+  /   |       +----+----+   |
|    | +    +    +--|         |   |
|    |/    /|    | +|         |   +
+    +----+ |    |/ +         +  / 
|         | +----+  |         | +  
|         |/        |         |/   
+----+----+         +----+----+

There are 78 millable pieces, including the 59 notchables - leaving 19 pieces that are millable but not notchable. Such pieces require cuts that parallel the long axis of the piece but are bounded on either end by a cut perpendicular to the long axis of the piece. Several of them have been used in existing named designs and are shown in the table of "other" pieces above. All 19 are shown below for reference. There are 9 mirror pairs and only one mirror symmetric piece, shown first and out of sequence for convenience. The pieces highlighted like this have not appeared in any of the named puzzles I mention, so could be considered the Obscure Millables.

160 M +----+ +----+----+ +----+ / /\| / /\| / /\| + + \| +----+----+ \| + + \| / / +--\| \| +-/ / + +----+ / \| \|/ +----+ \| \| \| + +----+----+ \| \| \| \| \|/ \| \| + + +----+----+----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+
88 M +----+ +----+ +----+----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +--\| \| +-/ / + +----+ / \| \|/ +----+----+ \| \| \| + +----+ \| \| \| \| \|/ \| \| + + +----+----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+	118 M +----+ +----+----+ / /\| / /\| + + \| +----+ + + \| / / +-/ /\|-+-/ / + +----+ / +----+ \| +----+----+ \| \| \| + \| \| + \| \| \| \| \|/ \| \|/ \| \| + + +----+ +----+ + / \| \| + \| \|/ +----+----+----+----+----+----+	192 M +----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +----+--\| \| +-/ / + +----+ / \| \|/ +----+ \| \| \| + +----+ \| \| \| \| \|/ \| \| + + +----+----+----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+	224 M +----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +--\| \| +----+-/ / + +----+ / \| \|/ +----+ \| \| \| + +----+ \| \| \| \| \|/ \| \| + + +----+----+----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+	399 M +----+----+----+----+ +----+ / /\| / /\| + +----+----+ \| + + \| / /\| \| +-/ / + +----+----+ \| \|/ +----+ \| \| \| + +----+ \| \| \| \| \| \| / \| \| + + + \| +----+----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+	536 M +----+ +----+----+----+----+ / /\| / /\| + + \| +----+----+ + \| / / +--\| / / + +----+ / \| +----+----+ \| \| \| + +----+ \| \| \| \| \|/ /\| \| \| + + +----+----+ \| + + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+
416 M +----+ +----+----+ +----+ / /\| / /\| / /\| + + \| +----+----+ \| + + \| / / +--\| \| +-/ / + +----+ / \| \|/ +----+ \| \| \| + + +----+ \| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+	672 M +----+ +----+----+ +----+ / /\| / /\| / /\| + + \| +----+----+ \| + + \| / / +--\| \| +-/ / + +----+ / \| \|/ +----+ \| \| \| + +----+ + \| \| \| \| \|/ /\| / \| \| + + +----+----+ \| +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+	431 M +----+----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +--\| \| +-/ / + +----+----+ / \| \|/ +----+ \| \| \| +----+----+ \| \| \| \| \| \| / \| \| + + + \| +----+----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+	600 M +----+ +----+ +----+----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +--\| \| +-/ / + +----+ / \| \|/ +----+----+ \| \| \| + +----+--\| \| \| \| \|/ /\| \| \| + + +----+----+ \| + + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+	448 M +----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +----+--\| \| +-/ / + +----+ / \| \|/ +----+ \| \| \| + +----+----+ \| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+	736 M +----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +--\| \| +----+-/ / + +----+ / \| \|/ +----+ \| \| \| + +----+----+ \| \| \| \| \|/ /\| / \| \| + + +----+----+ \| +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+
491 M +----+----+ +----+ / /\| / /\| + + \| +----+ + + \| / / +-/ /\|-+-/ / + +----+----+ / +----+ \| +----+ \| \| \| +--\| \| + \| \| \| \| \| \| \| \|/ \| \| + + + \| + +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+	630 M +----+ +----+----+ / /\| / /\| + + \| +----+ + + \| / / +-/ /\|-+-/ / + +----+ / +----+ \| +----+----+ \| \| \| + \| \| +--\| \| \| \| \|/ \| \| \| \| \| + + +----+ + \| + + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+	508 M +----+ +----+ / /\| / /\| + + \| +----+ + + \| / / +----+-/ /\|-+-/ / + +----+ / +----+ \| +----+ \| \| \| + +--\| \| + \| \| \| \| \|/ /\| \| \|/ \| \| + + +----+ \| + +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+	766 M +----+ +----+ / /\| / /\| + + \| +----+ + + \| / / +-/ /\|-+----+-/ / + +----+ / +----+ \| +----+ \| \| \| + \| \| +----+ \| \| \| \| \|/ \| \| \| / \| \| + + +----+ + \| +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+	1423 M +----+----+----+----+ +----+ / /\| / /\| + +----+----+ \| + + \| / /\| \| +-/ / + +----+----+ \| \|/ +----+ \| \| \| +----+----+ \| \| \| \| \| + / \| \| + + + / +----+----+ + / \| \| + \| \| + \| \|/ \| \|/ +----+----+ +----+----+----+	1513 M +----+----+ +----+ / /\| / /\| + +----+----+ + + \| / /\|-+-/ / + +----+----+----+----+ \| +----+ \| \| \| + \| \| \| \| \|/ \| \| + + +----+ +----+ + / \| \| + \| \| + \| \|/ \| \|/ +----+----+ +----+----+----+

Some Common Six-Piece Burr Designs

I have noticed the following four designs recur over and over again in different products.

They are: The Diabolical Structure (which really isn't all that diabolical), the Chinese Cross, the Six-Way Set, and the Yamato Block. It should be fairly easy for you to find contemporary examples using these pieces, and these four burr puzzles are a reasonable introduction to the category.

The Diabolical Structure

1 A A [p]

    +----+----+----+----+----+----+
   /                             /|
  +                             + |
 /                             /  +
+----+----+----+----+----+----+   |
|                             |   |
|                             |   +
+                             +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The Key

256 J X [p2]

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +                 |    |   |
|    |/                  |    |   +
+    +----+----+----+----+    +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The Tray

256 J X [p2]

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +                 |    |   |
|    |/                  |    |   +
+    +----+----+----+----+    +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The Tray

256 J X [p2]

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +                 |    |   |
|    |/                  |    |   +
+    +----+----+----+----+    +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The Tray

928 V L

    +----+    +----+----+    +----+
   /    /|   /         /|   /    /|
  +    + |  +----+----+ |  +    + |
 /    /  +--|         | +-/    /  +
+----+  /   |         |/ +----+   |
|    | +    +         +  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

The Tongue

928 V L

    +----+    +----+----+    +----+
   /    /|   /         /|   /    /|
  +    + |  +----+----+ |  +    + |
 /    /  +--|         | +-/    /  +
+----+  /   |         |/ +----+   |
|    | +    +         +  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

The Tongue

The pieces include: 1, 3x256, and 2x928 (AJ-VV-JJ or ALLXXX). The colorful burr from "Melissa & Doug" uses this set. It is very easy to construct - in fact this is possibly the easiest of all 6-piece burrs.

This set of pieces appeared in a French puzzle called Charpente Diabolique (the Diabolical Structure) - I finally obtained an example.

La Charpente Diabolique

Additional examples - the Adams Block Puzzle (which I do not own), and a Micro Burr in its own small box -
made by John Polhemus, sold via his wife's Etsy store Silly Sheila Designs.

The Chinese Cross

1 A A [p]

    +----+----+----+----+----+----+
   /                             /|
  +                             + |
 /                             /  +
+----+----+----+----+----+----+   |
|                             |   |
|                             |   +
+                             +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The Key

256 J X [p2]

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +                 |    |   |
|    |/                  |    |   +
+    +----+----+----+----+    +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The Tray

824 T R [p]

    +----+         +----+----+----+
   /    /|        /              /|
  +    + |       +----+         + |
 /    /  +----+--|   /         /  +
+----+  /        |  +----+----+   |
|    | +    +----+  |         |   |
|    |/    /|       |         |   +
+    +----+ |       +         +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

The

975 O Q [p]

    +----+----+----+         +----+
   /              /|        /    /|
  +         +----+ |       +    + |
 /         /|    | +----+-/    /  +
+----+----+ |    |/      +----+   |
|         | +    +----+  |    |   |
|         | |        /   |    |   +
+         + |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

Offsets

928 V L

    +----+    +----+----+    +----+
   /    /|   /         /|   /    /|
  +    + |  +----+----+ |  +    + |
 /    /  +--|         | +-/    /  +
+----+  /   |         |/ +----+   |
|    | +    +         +  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

The Tongue

1024 Y Y [p2]

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +    +----+----+  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

The Y

This set of pieces has been used often, and has appeared in ivory. Jurg von Kaenel refers to this as "the well-known one."

small red burr
This small plastic red burr is one of my older puzzles - I don't recall where I got it. Reiss Licorice Stix Reiss Licorice Stix pieces
Licorice Stix - Reiss (1974) plastic burr pendant (China)
This is a small plastic burr pendant, made in China.
Dohikus
This set also appeared as "Dohikus." (I don't have this.) Kong Ming Lock 28831
Kaiyue Kong Ming Lock Kongming Lock green
Another plastic version from China.
Colorful Wooden 6-piece traditional Burr
A colorful wooden version, from China.

The Six-Way Set

52 D P [p]

    +----+         +----+----+----+
   /    /|        /              /|
  +    + |       +              + |
 /    /  +----+-/              /  +
+----+  /      +----+----+----+   |
|    | +       |              |   |
|    |/        |              |   +
+    +----+----+              +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The Side Tray

792 R D

    +----+    +----+----+----+----+
   /    /|   /                   /|
  +    + |  +----+----+         + |
 /    /  +--|        /         /  +
+----+  /   |       +----+----+   |
|    | +    +       |         |   |
|    |/    /|       |         |   +
+    +----+ |       +         +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

The

911 N C

    +----+----+----+----+    +----+
   /                   /|   /    /|
  +         +----+----+ |  +    + |
 /         /|         | +-/    /  +
+----+----+ |         |/ +----+   |
|         | +         +  |    |   |
|         | |        /   |    |   +
+         + |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

Walls

824 T R [p]

    +----+         +----+----+----+
   /    /|        /              /|
  +    + |       +----+         + |
 /    /  +----+--|   /         /  +
+----+  /        |  +----+----+   |
|    | +    +----+  |         |   |
|    |/    /|       |         |   +
+    +----+ |       +         +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

The

975 O Q [p]

    +----+----+----+         +----+
   /              /|        /    /|
  +         +----+ |       +    + |
 /         /|    | +----+-/    /  +
+----+----+ |    |/      +----+   |
|         | +    +----+  |    |   |
|         | |        /   |    |   +
+         + |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

Offsets

1024 Y Y [p2]

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +    +----+----+  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

The Y

This is the only notchable, voidless set that can be put together six different ways.

aluminum burr - Bits and Pieces
I got this aluminum burr called "Rainbow" from Bits and Pieces - it came in a nice black drawstring pouch. It was designed by Paul Eibe. DNORTY - Pentangle
This is DNORTY from Pentangle. The name derives from the bold piece letters given in my table above: 52 (D), 911 (N), 975 (O), 792 (R), 824 (T), 1024 (Y). Tongari Kun and Roppongi - Toyo (Mike Green)
This is a Toyo Glass puzzle called "Tongari Kun and Roppongi." Not only is there a burr, but it must be assembled inside the glass container. The mouth is too small to pass the burr in fully assembled form. Remember, there are 6 different ways to construct this burr - you must find one that permits construction within the container!

This set was sold some time ago (perhaps prior to 1900) as The ZOOZZLER. If you look carefully at the inside of the box lid shown in the photo on the left, you'll see the Zoozzler came from the La Rose Manufacturing Company of Albany, N.Y.
In December 2008 I was contacted by Pete Brady, who discovered a Zoozzler in the back of an old desk, and after assembling it, did a Google search on it and found my website. Pete's copy is shown on the right.
Pete, who is now in his 70's (and still solving burr puzzles!) tells me that his grandfather was Anthime F. La Rose, who was born in 1842 in a small town near Montreal, and who died in 1920. Anthime was raised in French Canada and eventually emigrated to Albany, where he established his factory at 172 Broadway and made, among other things like the Zoozzler, furniture, and phone booths for Western Electric. There is no evidence of any patent, though the box does carry the words "Trade Mark" - Pete believes that Anthime produced the Zoozzler in his well-equipped factory. The box says, "Agents wanted to sell the ZOOZZLER in every town or city - liberal commission. Special inducements to boys and girls to sell in their spare time." No phone number appears on any of the packaging, so it may be that the Zoozzler was produced prior to 1900.
Pete says his grandfather was married twice. After his first wife died, Anthime married Julia, who was born in 1863 and died in 1945, and in 1899 had a daughter, Katharine, who was Pete's mother.
Thanks for the info, Pete, and for allowing me to share it! I find this kind of historical background adds a lot to my enjoyment of puzzles. It is not always easy to feel any connection to our distant ancestors, but a puzzle can be a tangible link to the past.

I finally found an original example of the Zoozzler puzzle in its box:

The Zoozzler

To resolve all six different solutions, I found it helpful to ask myself, "What sits in the notch of piece #52, and then which piece is opposite #52?" I found the following:

left offset 824, right wall 911 - this seems like it fits together, but is in fact not constructible. This is a good illustration of what is meant by an apparent assembly.

left offset 824, right offset 975 - two 3-pc halves slide together
right offset 975, left offset 824 - mirror of the above
right wall 911, left offset 824
right wall 911, left wall 792
left wall 792, right offset 975
left wall 792, right wall 911

The Yamato Block

1 A A [p]

    +----+----+----+----+----+----+
   /                             /|
  +                             + |
 /                             /  +
+----+----+----+----+----+----+   |
|                             |   |
|                             |   +
+                             +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The Key

188 I M [p]

    +----+         +----+    +----+
   /    /|        /    /|   /    /|
  +    + |       +    + |  +    + |
 /    /  +----+-/    /  +-/    /  +
+----+  /      +----+  / +----+   |
|    | +       |    | +  |    |   |
|    |/        |    |/   |    |   +
+    +----+----+    +----+    +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The (Bottle) Opener

824 T R [p]

    +----+         +----+----+----+
   /    /|        /              /|
  +    + |       +----+         + |
 /    /  +----+--|   /         /  +
+----+  /        |  +----+----+   |
|    | +    +----+  |         |   |
|    |/    /|       |         |   +
+    +----+ |       +         +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

The

975 O Q [p]

    +----+----+----+         +----+
   /              /|        /    /|
  +         +----+ |       +    + |
 /         /|    | +----+-/    /  +
+----+----+ |    |/      +----+   |
|         | +    +----+  |    |   |
|         | |        /   |    |   +
+         + |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

Offsets

1024 Y Y [p2]

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +    +----+----+  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

The Y

1024 Y Y [p2]

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +    +----+----+  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

The Y

The vintage Japanese Yamato Block Puzzle.	This is "No. P19 Joe's Puzzle" from Wm. F. Drueke & Sons of Grand Rapids Michigan. There is no date on the box but it seems fairly old.	This is a small brass burr, called the "Ultimate Puzzle," made for Chadwick Miller and dated 1969. It came with a small black case with a question mark on the front.
In this aluminum burr, piece 824 is fixed to the base. I think this came from B&P.
The Rungsted Puzzler - two instances of a small brass burr with instruction sheet. Made in Denmark. The Yamato Block pieces { 1, 188, 824/975, 1024x2 } The same small brass burr was sold by Chadwick Miller as the Ultimate Puzzle, and they used a similar question mark symbol.
Interlock - a vintage puzzle from Crestline No year on the box. This is a large example of the Yamato Block set of pieces { 1, 188, 824/975, 2x 1024 }.

More Six-Piece Burrs

Love's Dozen

    +----+    +----+    +----+----+
   /    /|   /    /|   /         /|
  +    + |  +----+ |  +         + |
 /    /  +--|    | +-/         /  +
+----+  /   |    |/ +----+----+   |
|    | +    +----+  |         |   |
|    |/             |         |   +
+    +----+----+----+         +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

512

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +    +----+       |    |   |
|    |/    /|   /        |    |   +
+    +----+ |  +----+----+    +  / 
|         | +--|              | +  
|         |/   |              |/   
+----+----+    +----+----+----+

704

    +----+         +----+    +----+
   /    /|        /    /|   /    /|
  +    + |       +----+ |  +    + |
 /    /  +----+--|    | +-/    /  +
+----+  /        |    |/ +----+   |
|    | +         +    +  |    |   |
|    |/         /|   /   |    |   +
+    +----+----+ |  +----+    +  / 
|              | +--|         | +  
|              |/   |         |/   
+----+----+----+    +----+----+

960

    +----+         +----+    +----+
   /    /|        /    /|   /    /|
  +    + |       +----+ |  +    + |
 /    /  +-------|    | +-/    /  +
+----+  /        |    |/ +----+   |
|    | +    +----+    +  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

992

    +----+    +----+         +----+
   /    /|   /    /|        /    /|
  +    + |  +----+ |       +    + |
 /    /  +--|    | +----+-/    /  +
+----+  /   |    |/      +----+   |
|    | +    +    +----+  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

1008

    +----+----+              +----+
   /         /|             /    /|
  +    +----+ |            +    + |
 /    /|    | +----+----+-/    /  +
+----+ |    |/           +----+   |
|    | +----+----+----+  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

This is Bruce Love's Dozen, (the version without the D's) purchased from Bill Cutler, and made from Maple by Jerry McFarland. This burr is special because it is the only burr at the highest level, 12. Unfortunately the solution is not unique - there are 89 ways to put these pieces together, and most of them don't achieve level 12. Note that there are no other level 12 burrs (for any length stick), and no level 11 burrs at all.

The Piston Burr

    +----+    +----+    +----+----+
   /    /|   /    /|   /         /|
  +    + |  +----+ |  +         + |
 /    /  +--|    | +-/         /  +
+----+  /   |    |/ +----+----+   |
|    | +    +----+  |         |   |
|    |/             |         |   +
+    +----+----+----+         +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

512

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +    +----+       |    |   |
|    |/    /|   /        |    |   +
+    +----+ |  +----+----+    +  / 
|         | +--|              | +  
|         |/   |              |/   
+----+----+    +----+----+----+

768

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +         +----+  |    |   |
|    |/         /|   /   |    |   +
+    +----+----+ |  +----+    +  / 
|              | +--|         | +  
|              |/   |         |/   
+----+----+----+    +----+----+

922

    +----+    +----+----+    +----+
   /    /|   /         /|   /    /|
  +    + |  +         + |  +    + |
 /    /  +-/         /  +-/    /  +
+----+  / +----+----+  / +----+   |
|    | +  |         | +  |    |   |
|    |/   |         |/   |    |   +
+    +----+----+----+----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

1008

    +----+----+              +----+
   /         /|             /    /|
  +    +----+ |            +    + |
 /    /|    | +----+----+-/    /  +
+----+ |    |/           +----+   |
|    | +----+----+----+  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

1008

    +----+----+              +----+
   /         /|             /    /|
  +    +----+ |            +    + |
 /    /|    | +----+----+-/    /  +
+----+ |    |/           +----+   |
|    | +----+----+----+  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

This is Peter Marineau's "Piston" burr, so named because of the large number of times pieces must be moved back and forth during the solution. This burr is special because it achieves the highest level possible for length-6 pieces, level 9 (i.e. it requires 9 moves to release the first piece), and the solution is unique - it has no other solutions at lower levels.

I made an example from Lego. I also bought a version made from six exotic woods, by Thomas Moeller. It is quite large - each piece measures 1.5" x 1.5" x 4.5".

Check Bill Cutler's site for availability.

Computer's Choice Unique 10

624

    +----+----+         +----+----+
   /         /|        /         /|
  +    +----+ |       +----+    + |
 /    /|    | +----+--|   /    /  +
+----+ |    |/        |  +----+   |
|    | +----+    +----+--|    |   |
|    |/         /|   /   |    |   +
+    +----+----+ |  +----+    +  / 
|              | +--|         | +  
|              |/   |         |/   
+----+----+----+    +----+----+

702

    +----+         +----+    +----+
   /    /|        /    /|   /    /|
  +    + |  +----+----+ |  +    + |
 /    /  +-/    /|    | +-/    /  +
+----+  / +----+ |    |/ +----+   |
|    | +  |    | +    +  |    |   |
|    |/   |    | |   /   |    |   +
+    +----+    + |  +----+    +  / 
|              | +--|         | +  
|              |/   |         |/   
+----+----+----+    +----+----+

768

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +         +----+  |    |   |
|    |/         /|   /   |    |   +
+    +----+----+ |  +----+    +  / 
|              | +--|         | +  
|              |/   |         |/   
+----+----+----+    +----+----+

883

    +----+              +----+----+
   /    /|             /         /|
  +    +----+    +----+         + |
 /         /|-+-/              /  +
+----+----+ |  +----+----+----+   |
|         | +--|              |   |
|         | |  |              |   +
+         + |  +----+         +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

1015

    +----+                   +----+
   /    /|                  /    /|
  +    +----+         +----+    + |
 /         /|-+----+-/         /  +
+----+----+ |       +----+----+   |
|         | +----+--|         |   |
|         | |       |         |   +
+         + |       +         +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

1024 Y Y [p2]

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +    +----+----+  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

The Y

This is Bill Cutler's Computer's Choice Unique 10 burr. I don't know who the craftsman is - I bought it as part of a group of hand-made puzzles. This burr is special because it is one of 18 burrs that have a unique level 10 solution, the highest level achievable for six-piece burrs with unique solutions. The pieces must be length-8, however, not length-6.

The Baffling Burr Puzzle (Bill Cutler's #305)

52 D P [p]

    +----+         +----+----+----+
   /    /|        /              /|
  +    + |       +              + |
 /    /  +----+-/              /  +
+----+  /      +----+----+----+   |
|    | +       |              |   |
|    |/        |              |   +
+    +----+----+              +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The Side Tray

615 K G 1

    +----+----+    +----+----+----+
   /         /|   /              /|
  +         + |  +----+         + |
 /         /  +--|   /         /  +
+----+----+  /   |  +----+----+   |
|         | +----+  |         |   |
|         | |       |         |   +
+         + |       +         +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

Left Notched Half-Tray

792 R D 2

    +----+    +----+----+----+----+
   /    /|   /                   /|
  +    + |  +----+----+         + |
 /    /  +--|        /         /  +
+----+  /   |       +----+----+   |
|    | +    +       |         |   |
|    |/    /|       |         |   +
+    +----+ |       +         +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

Left Wall

960 X N 2

    +----+         +----+    +----+
   /    /|        /    /|   /    /|
  +    + |       +----+ |  +    + |
 /    /  +-------|    | +-/    /  +
+----+  /        |    |/ +----+   |
|    | +    +----+    +  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

The

992 W O [p] 2

    +----+    +----+         +----+
   /    /|   /    /|        /    /|
  +    + |  +----+ |       +    + |
 /    /  +--|    | +----+-/    /  +
+----+  /   |    |/      +----+   |
|    | +    +    +----+  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

Fingers

975 O Q E [p] 2

    +----+----+----+         +----+
   /              /|        /    /|
  +         +----+ |       +    + |
 /         /|    | +----+-/    /  +
+----+----+ |    |/      +----+   |
|         | +    +----+  |    |   |
|         | |        /   |    |   +
+         + |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

Right Offset

This is called The Baffling Burr Puzzle ("Six interlocked pieces of wood that will challenge the experts") - there is no other information on the box. This has pieces numbers 52, 615, 792, 960/992, 975 and is Bill Cutler's #305, not Bill's Baffling Burr, which has pieces 103, 760, 960/992, 996, 1024.

Eight is Enough - Bill Cutler

216

    +----+    +----+         +----+
   /    /|   /    /|        /    /|
  +    + |  +----+ |  +----+    + |
 /    /  +--|    | +-/         /  +
+----+  /   |    |/ +----+----+   |
|    | +    +----+  |         |   |
|    |/             |         |   +
+    +----+----+----+         +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

412

    +----+    +----+----+    +----+
   /    /|   /         /|   /    /|
  +    + |  +----+    + |  +    + |
 /    /  +--|   /    /  +-/    /  +
+----+  /   |  +----+  / +----+   |
|    | +    +  |    | +  |    |   |
|    |/    /|  |    |/   |    |   +
+    +----+ |  +    +----+    +  / 
|         | +--|              | +  
|         |/   |              |/   
+----+----+    +----+----+----+

751

    +----+----+              +----+
   /         /|             /    /|
  +         + |            +    + |
 /         /  +----+----+-/    /  +
+----+----+  /           +----+   |
|         | +    +----+  |    |   |
|         |/    /|   /   |    |   +
+         +----+ |  +----+    +  / 
|              | +--|         | +  
|              |/   |         |/   
+----+----+----+    +----+----+

896

    +----+              +----+----+
   /    /|             /         /|
  +    + |            +----+    + |
 /    /  +----+----+--|   /    /  +
+----+  /             |  +----+   |
|    | +    +----+----+--|    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

960

    +----+         +----+    +----+
   /    /|        /    /|   /    /|
  +    + |       +----+ |  +    + |
 /    /  +-------|    | +-/    /  +
+----+  /        |    |/ +----+   |
|    | +    +----+    +  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

Right Finger

1024

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +    +----+----+  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

The Y

This is Eight is Enough designed by Bill Cutler and made by Jerry McFarland.
It was Bill's IPP29 Exchange puzzle.
The pieces are length 8.

Toys From Times Past Burr Puzzle (Hoffmann Burr)

1 A A [p]

    +----+----+----+----+----+----+
   /                             /|
  +                             + |
 /                             /  +
+----+----+----+----+----+----+   |
|                             |   |
|                             |   +
+                             +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The Key

188 I M [p]

    +----+         +----+    +----+
   /    /|        /    /|   /    /|
  +    + |       +    + |  +    + |
 /    /  +----+-/    /  +-/    /  +
+----+  /      +----+  / +----+   |
|    | +       |    | +  |    |   |
|    |/        |    |/   |    |   +
+    +----+----+    +----+    +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The (Bottle) Opener

256 J X B [p2] 3

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +                 |    |   |
|    |/                  |    |   +
+    +----+----+----+----+    +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The Tray

960 X N 2

    +----+         +----+    +----+
   /    /|        /    /|   /    /|
  +    + |       +----+ |  +    + |
 /    /  +-------|    | +-/    /  +
+----+  /        |    |/ +----+   |
|    | +    +----+    +  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

Right Finger

975 O Q E [p] 2

    +----+----+----+         +----+
   /              /|        /    /|
  +         +----+ |       +    + |
 /         /|    | +----+-/    /  +
+----+----+ |    |/      +----+   |
|         | +    +----+  |    |   |
|         | |        /   |    |   +
+         + |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

Right Offset

1024 Y Y [p2]

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +    +----+----+  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

The Y

This is the Burr Puzzle from Toys From Times Past. This has pieces 1, 188, 256, 960, 975, 1024 and is the same design shown in Hoffmann, except Toys From Times Past has incorporated a locking mechanism into the key piece.

Philippe Dubois/Gaby Games

120 G U 1

    +----+              +----+----+
   /    /|             /         /|
  +    + |            +         + |
 /    /  +----+---+--/         /  +
+----+  /           +----+----+   |
|    | +            |         |   |
|    |/             |         |   +
+    +----+----+----+         +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The Three-Quarters Tray

160

    +----+    +----+----+    +----+
   /    /|   /         /|   /    /|
  +    + |  +----+----+ |  +    + |
 /    /  +--|         | +-/    /  +
+----+  /   |         |/ +----+   |
|    | +    +----+----+  |    |   |
|    |/                  |    |   +
+    +----+----+----+----+    +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

256 J X B [p2] 3

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +                 |    |   |
|    |/                  |    |   +
+    +----+----+----+----+    +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The Tray

512

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +    +----+       |    |   |
|    |/    /|   /        |    |   +
+    +----+ |  +----+----+    +  / 
|         | +--|              | +  
|         |/   |              |/   
+----+----+    +----+----+----+

880

    +----+----+         +----+----+
   /         /|        /         /|
  +    +----+ |       +----+    + |
 /    /|    | +----+--|   /    /  +
+----+ |    |/        |  +----+   |
|    | +----+----+----+--|    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

960 X N 2

    +----+         +----+    +----+
   /    /|        /    /|   /    /|
  +    + |       +----+ |  +    + |
 /    /  +-------|    | +-/    /  +
+----+  /        |    |/ +----+   |
|    | +    +----+    +  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

This small black plastic burr I found in a puzzle shop in Prague during IPP28 is a copy of the Philippe Dubois/Gaby Games burr that requires 6 (or 7, depending on how you count) moves to release the first piece. It is one of the "Fearsome Four."

The Arjeu CT757 is another example of this construction.

Arjeu CT757

Tenyo Brother

463

    +----+----+----+         +----+
   /              /|        /    /|
  +         +----+ |       +    + |
 /         /|    | +----+-/    /  +
+----+----+ |    |/      +----+   |
|         | +    +       |    |   |
|         | |   /        |    |   +
+         + |  +----+----+    +  / 
|         | +--|              | +  
|         |/   |              |/   
+----+----+    +----+----+----+

564

    +----+         +----+----+----+
   /    /|        /              /|
  +    + |       +              + |
 /    /  +----+-/              /  +
+----+  /      +----+----+----+   |
|    | +       |              |   |
|    |/        |              |   +
+    +----+----+----+         +  / 
|              | +--|         | +  
|              |/   |         |/   
+----+----+----+    +----+----+

760

    +----+                   +----+
   /    /|                  /    /|
  +    + |            +----+    + |
 /    /  +----+----+-/         /  +
+----+  /           +----+----+   |
|    | +         +--|         |   |
|    |/         /|  |         |   +
+    +----+----+ |  +         +  / 
|              | +--|         | +  
|              |/   |         |/   
+----+----+----+    +----+----+

909

    +----+----+----+----+    +----+
   /                   /|   /    /|
  +              +----+ |  +    + |
 /              /|    | +-/    /  +
+----+----+----+ |    |/ +----+   |
|              | +    +  |    |   |
|              |/    /   |    |   +
+         +----+    +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

927

    +----+    +----+----+    +----+
   /    /|   /         /|   /    /|
  +    +----+----+----+ |  +    + |
 /         /|         | +-/    /  +
+----+----+ |         |/ +----+   |
|         | +         +  |    |   |
|         | |        /   |    |   +
+         + |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

1016

    +----+                   +----+
   /    /|                  /    /|
  +    + |            +----+    + |
 /    /  +----+----+-/         /  +
+----+  /           +----+----+   |
|    | +    +----+--|         |   |
|    |/    /|       |         |   +
+    +----+ |       +         +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

I bought this plastic burr in Japan. I believe it was made by Tenyo. It is number 4 in a "Family" of burrs - this one is called "Brother." This burr uses six general pieces: 463, 564, 760, 909, 927, 1016. It has no holes, and comes apart in one move into two 3-piece halves.

This might be #72 in Filipiak's list (c.f. Anthony S. Filipiak, 100 Puzzles - How to Make and Solve Them, 1942, p. 86).

Kozy Kitajima's 6+6=Cube

1 A A [p]

    +----+----+----+----+----+----+
   /                             /|
  +                             + |
 /                             /  +
+----+----+----+----+----+----+   |
|                             |   |
|                             |   +
+                             +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The Key

188 I M [p]

    +----+         +----+    +----+
   /    /|        /    /|   /    /|
  +    + |       +    + |  +    + |
 /    /  +----+-/    /  +-/    /  +
+----+  /      +----+  / +----+   |
|    | +       |    | +  |    |   |
|    |/        |    |/   |    |   +
+    +----+----+    +----+    +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The (Bottle) Opener

256 J X B [p2] 3

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +                 |    |   |
|    |/                  |    |   +
+    +----+----+----+----+    +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The Tray

911 N C G 2

    +----+----+----+----+    +----+
   /                   /|   /    /|
  +         +----+----+ |  +    + |
 /         /|         | +-/    /  +
+----+----+ |         |/ +----+   |
|         | +         +  |    |   |
|         | |        /   |    |   +
+         + |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

1024 Y Y [p2]

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +    +----+----+  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

The Y

1024 Y Y [p2]

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +    +----+----+  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

The Y

52 D P [p]

    +----+         +----+----+----+
   /    /|        /              /|
  +    + |       +              + |
 /    /  +----+-/              /  +
+----+  /      +----+----+----+   |
|    | +       |              |   |
|    |/        |              |   +
+    +----+----+              +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The Side Tray

103 F S H 1

    +----+----+         +----+----+
   /         /|        /         /|
  +         + |       +         + |
 /         /  +---+--/         /  +
+----+----+  /      +----+----+   |
|         | +       |         |   |
|         |/        |         |   +
+         +----+----+         +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The Half-Tray

120 G U 1

    +----+              +----+----+
   /    /|             /         /|
  +    + |            +         + |
 /    /  +----+---+--/         /  +
+----+  /           +----+----+   |
|    | +            |         |   |
|    |/             |         |   +
+    +----+----+----+         +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The Three-Quarters Tray

928 V L D 2

    +----+    +----+----+    +----+
   /    /|   /         /|   /    /|
  +    + |  +----+----+ |  +    + |
 /    /  +--|         | +-/    /  +
+----+  /   |         |/ +----+   |
|    | +    +         +  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

The Tongue

960 X N 2

    +----+         +----+    +----+
   /    /|        /    /|   /    /|
  +    + |       +----+ |  +    + |
 /    /  +-------|    | +-/    /  +
+----+  /        |    |/ +----+   |
|    | +    +----+    +  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

The

992 W O [p] 2

    +----+    +----+         +----+
   /    /|   /    /|        /    /|
  +    + |  +----+ |       +    + |
 /    /  +--|    | +----+-/    /  +
+----+  /   |    |/      +----+   |
|    | +    +    +----+  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

Fingers

This set of twelve pieces is called the "6+6=Cube." It was designed by Kozy Kitajima. The pieces include: 1, 52, 103, 120, 188, 256, 911, 928, 992, 960, and 2x 1024. According to the instructions, there is only one way to build two burrs at once. The twelve pieces can also be combined to form a cube, with holes.

G4 or "The Cross of Marseille"

1 A A [p]

    +----+----+----+----+----+----+
   /                             /|
  +                             + |
 /                             /  +
+----+----+----+----+----+----+   |
|                             |   |
|                             |   +
+                             +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The Key

188 I M [p]

    +----+         +----+    +----+
   /    /|        /    /|   /    /|
  +    + |       +    + |  +    + |
 /    /  +----+-/    /  +-/    /  +
+----+  /      +----+  / +----+   |
|    | +       |    | +  |    |   |
|    |/        |    |/   |    |   +
+    +----+----+    +----+    +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The (Bottle) Opener

512

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +    +----+       |    |   |
|    |/    /|   /        |    |   +
+    +----+ |  +----+----+    +  / 
|         | +--|              | +  
|         |/   |              |/   
+----+----+    +----+----+----+

832

    +----+         +----+----+----+
   /    /|        /              /|
  +    + |       +----+----+    + |
 /    /  +----+--|        /    /  +
+----+  /        |       +----+   |
|    | +    +----+    +--|    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

975 O Q [p]

    +----+----+----+         +----+
   /              /|        /    /|
  +         +----+ |       +    + |
 /         /|    | +----+-/    /  +
+----+----+ |    |/      +----+   |
|         | +    +----+  |    |   |
|         | |        /   |    |   +
+         + |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

Offsets

1024 Y Y [p2]

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +    +----+----+  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

The Y

1 A A [p]

    +----+----+----+----+----+----+
   /                             /|
  +                             + |
 /                             /  +
+----+----+----+----+----+----+   |
|                             |   |
|                             |   +
+                             +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The Key

188 I M [p]

    +----+         +----+    +----+
   /    /|        /    /|   /    /|
  +    + |       +    + |  +    + |
 /    /  +----+-/    /  +-/    /  +
+----+  /      +----+  / +----+   |
|    | +       |    | +  |    |   |
|    |/        |    |/   |    |   +
+    +----+----+    +----+    +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The (Bottle) Opener

768

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +         +----+  |    |   |
|    |/         /|   /   |    |   +
+    +----+----+ |  +----+    +  / 
|              | +--|         | +  
|              |/   |         |/   
+----+----+----+    +----+----+

976

    +----+----+----+         +----+
   /              /|        /    /|
  +    +----+----+ |       +    + |
 /    /|         | +----+-/    /  +
+----+ |         |/      +----+   |
|    | +----+    +----+  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

824 T R C [p] 2

    +----+         +----+----+----+
   /    /|        /              /|
  +    + |       +----+         + |
 /    /  +----+--|   /         /  +
+----+  /        |  +----+----+   |
|    | +    +----+  |         |   |
|    |/    /|       |         |   +
+    +----+ |       +         +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

Offsets

1024 Y Y [p2]

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +    +----+----+  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

The Y

This burr's wooden length-12 pieces are stained a dark color. The burr comes in a box with a fitted slip-out cover. At some point I saw it referred to as "G4," also as "The Cross of Marseille." The pieces used are: 1, 188, 512, 832, 975, 1024. The mirror images of the 3rd-5th can also be used: 1, 188, 768, 976, 824, 1024.

Grandfather's Puzzle - a vintage wooden traditional six-piece burr.
No provenance - no other markings on the box or pieces.
The pieces are { 1, 188, 768, 824, 976, 1024 } - the "Cross of Marseille" set.

Here is a vintage hand-made version with knobs decorating the piece ends.

Super Stumpa - a vintage plastic six-piece burr from Executive Games.
The pieces are { 1, 188, 512, 832, 975, 1024 } - the "Cross of Marseille" set.
The instruction sheet mentions other interesting puzzles, including the
"Barry Pitt Original Third Dimension Stumpa" that resembles a Paracelsus Puzzle.

The Avenger

240

    +----+----+              +----+
   /         /|             /    /|
  +    +----+ |            +    + |
 /    /|    | +----+----+-/    /  +
+----+ |    |/           +----+   |
|    | +----+            |    |   |
|    |/                  |    |   +
+    +----+----+----+----+    +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

768

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +         +----+  |    |   |
|    |/         /|   /   |    |   +
+    +----+----+ |  +----+    +  / 
|              | +--|         | +  
|              |/   |         |/   
+----+----+----+    +----+----+

960 X N 2

    +----+         +----+    +----+
   /    /|        /    /|   /    /|
  +    + |       +----+ |  +    + |
 /    /  +-------|    | +-/    /  +
+----+  /        |    |/ +----+   |
|    | +    +----+    +  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

984

    +----+    +----+         +----+
   /    /|   /    /|        /    /|
  +    + |  +----+ |  +----+    + |
 /    /  +--|    | +-/         /  +
+----+  /   |    |/ +----+----+   |
|    | +    +    +--|         |   |
|    |/    /|       |         |   +
+    +----+ |       +         +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

1024 Y Y [p2]

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +    +----+----+  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

The Y

1933

    +----+----+----+----+    +----+
   /                   /|   /    /|
  +              +----+ |  +    + |
 /              /|    | +-/    /  +
+----+----+----+ |    |/ +----+   |
|              | +    +  |    |   |
|              |/|   /   |    |   +
+         +----+ |  +----+    +  / 
|         | +    +--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

The Avenger is offered by PuzzleMaster.ca. It includes 9 length-10 pieces, one of which (their #1) is not traditionally notched. Subsets of the pieces can be assembled into six-piece, seven-piece, eight-piece, and nine-piece burrs. The pieces are:

1 2 3 4 5 6 7 8 9
non trad. 896 928 240 1024 768 984 960 1933

For the six-piece assembly the pieces used are: 240, 768, 960, 984, 1024, 1933.

The Double-Cross Puzzle

1 A A [p]

    +----+----+----+----+----+----+
   /                             /|
  +                             + |
 /                             /  +
+----+----+----+----+----+----+   |
|                             |   |
|                             |   +
+                             +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The Key

154 H K I [p] 1

    +----+    +----+----+    +----+
   /    /|   /         /|   /    /|
  +    + |  +         + |  +    + |
 /    /  +-/         /  +-/    /  +
+----+  / +----+----+  / +----+   |
|    | +  |         | +  |    |   |
|    |/   |         |/   |    |   +
+    +----+         +----+    +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The Toaster

256 J X B [p2] 3

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +                 |    |   |
|    |/                  |    |   +
+    +----+----+----+----+    +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The Tray

256 J X B [p2] 3

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +                 |    |   |
|    |/                  |    |   +
+    +----+----+----+----+    +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The Tray

1024 Y Y [p2]

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +    +----+----+  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

The Y

1024 Y Y [p2]

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +    +----+----+  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

The Y

This is The Double-Cross Puzzle, issued by the General Engineering & Design Co. of Detroit, Michigan. (No date.) Six metal pieces. A very easy design.

Double-Cross Puzzle - General Engineering & Design Co.

The Artifactory 5-4 Puzzle

412 N

    +----+    +----+----+    +----+
   /    /|   /         /|   /    /|
  +    + |  +----+    + |  +    + |
 /    /  +--|   /    /  +-/    /  +
+----+  /   |  +----+  / +----+   |
|    | +    +  |    | +  |    |   |
|    |/    /|  |    |/   |    |   +
+    +----+ |  +    +----+    +  / 
|         | +--|              | +  
|         |/   |              |/   
+----+----+    +----+----+----+

480 N

    +----+    +----+         +----+
   /    /|   /    /|        /    /|
  +    + |  +----+ |       +    + |
 /    /  +--|    | +----+-/    /  +
+----+  /   |    |/      +----+   |
|    | +    +    +       |    |   |
|    |/    /|   /        |    |   +
+    +----+ |  +----+----+    +  / 
|         | +--|              | +  
|         |/   |              |/   
+----+----+    +----+----+----+

512 N

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +    +----+       |    |   |
|    |/    /|   /        |    |   +
+    +----+ |  +----+----+    +  / 
|         | +--|              | +  
|         |/   |              |/   
+----+----+    +----+----+----+

704 N

    +----+         +----+    +----+
   /    /|        /    /|   /    /|
  +    + |       +----+ |  +    + |
 /    /  +----+--|    | +-/    /  +
+----+  /        |    |/ +----+   |
|    | +         +    +  |    |   |
|    |/         /|   /   |    |   +
+    +----+----+ |  +----+    +  / 
|              | +--|         | +  
|              |/   |         |/   
+----+----+----+    +----+----+

704 N

    +----+         +----+    +----+
   /    /|        /    /|   /    /|
  +    + |       +----+ |  +    + |
 /    /  +----+--|    | +-/    /  +
+----+  /        |    |/ +----+   |
|    | +         +    +  |    |   |
|    |/         /|   /   |    |   +
+    +----+----+ |  +----+    +  / 
|              | +--|         | +  
|              |/   |         |/   
+----+----+----+    +----+----+

960 X N 2

    +----+         +----+    +----+
   /    /|        /    /|   /    /|
  +    + |       +----+ |  +    + |
 /    /  +-------|    | +-/    /  +
+----+  /        |    |/ +----+   |
|    | +    +----+    +  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

The 5-4 Burr - handmade by Artifactory in Oregon
An auction buy-it-now for $40 - the seller says they are the exclusive online distributor.
Nice exotic woods in a good size - but a very loose fit.
The woods are: wenge, yellowheart, maple, zebrawood, bloodwood, and purpleheart.
I took a chance on this since they didn't show the pieces, and I am pleased since it turns out
this is an instance of David Winkler's complex 5.4, which I didn't have.
The pieces are { 412, 480, 512, 704x2, 960 }.

Miscellaneous

Here is a group of miscellaneous burrs I've accumulated.

Burr group burr pieces A burr pieces B burr pieces C,D
The light brown burr is perhaps the more difficult of this group, but we've seen it already - its pieces are the familiar "Six Way" set: 52, 792/911, 824/975, 1024.
The white and two (identical) dark brown burrs all employ the familiar "Chinese Cross" piece set: 1, 256, 824/975, 928, 1024.

Burr Sets

Obviously it would be nice to have a set of pieces all with consistent dimensions, in order to conveniently try different burr designs.

There have been several wooden sets produced, of varying completeness and quality. Wayne Daniel and Pentangle both at one point offered sets of 42, but they're not being produced any more as far as I know. Dick Wetters also offered sets, but he, too, has stopped.

I made generic burr pieces (6x #1024, each requiring 14 cubes) from LiveCube. Then, with 20 extra pieces (here in yellow), one can build any of the possible burr pieces, and any set of six to try a particular burr.

In 2008 I noticed that a Chinese fellow named (I believe) Qiu Jinhua received an award and a patent for the same idea! See this Chinese website at www.eipm.com.tw for information on his "Universal Lubanga Lock." If you translate the page using Google, you'll note that the description text sounds like my introductory text to this section on traditional six-piece burrs. The LiveCube example shown even uses yellow cubes for the interior. Check out the Internet Archive "Wayback Machine" and take a look at the snapshot of my website from October of 2004 to see that I had this idea pretty early on. Hmmm. Can you say, "prior art?"

Puzzlist Aaron Siegel has created several wonderful resources for the mechanical puzzle community. If you have access to a 3D printer, your best bet as of this writing (May 2020) to obtain a burr piece set is to check out Aaron Siegel's Starter Burr Set, and Extensible Burr Set, both at Thingiverse.

Aaron has also created Puzzlecad - An OpenSCAD library for interlocking puzzles, and the Printable Puzzle Project at puzzlehub.org, where you can find plans for many other mechanical puzzles, including designs by Stewart Coffin, Yavuz Demirhan, Laszlo Molnar, Christoph Lohe, and Alfons Eyckmans.

I received this 3D printed set of 24 pieces (Starter + Expansion):

Starter Burr Set + Expansion - Aaron Siegel

Professor Burr Set - Hansen SF, Yamanaka Kumiki Works Japan

On the left is a "Professor" burr set from the Yamanaka Kumiki Works in Japan.
Its twelve length-8 pieces can be used to assemble at least four different traditional 6-piece burrs.
The set includes only notchable pieces:

1, 18, 52, 154, 188, 256 x2, 824/975, 992, 1024 x2.

The Professional Puzzle set (also produced by Yamanaka Kumiki Works) on the right is identical.

Yamanaka also produced a set "No. 3505" called "Let's Shap the Fascinating World!!" (sic). That set includes almost the same 12 pieces as the Professional set, except instead of 18 and 52, the two pieces 512 and 832 appear.

The instructions provide four puzzles and the first two are identical to the Professional set's.
The third is equal to "G4" { 1, 188, 512, 832, 975, 1024 }.
The fourth I hadn't seen listed before: { 1, 188, 256, 512, 832, 992 }.

Here is another set produced by the Yamanaka Kumiki Works - four classic traditional six-piece burrs, colored black, yellow, green, and orange.
I had seen these in other collections and thought them long out of production, but I was able to purchase a new set on auction very reasonably.

Yamanaka Burr Set

Black: 1, 188, 256, 824, 992, 1024

1 A A [p]

    +----+----+----+----+----+----+
   /                             /|
  +                             + |
 /                             /  +
+----+----+----+----+----+----+   |
|                             |   |
|                             |   +
+                             +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The Key

188 I M [p]

    +----+         +----+    +----+
   /    /|        /    /|   /    /|
  +    + |       +    + |  +    + |
 /    /  +----+-/    /  +-/    /  +
+----+  /      +----+  / +----+   |
|    | +       |    | +  |    |   |
|    |/        |    |/   |    |   +
+    +----+----+    +----+    +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The (Bottle) Opener

256 J X B [p2] 3

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +                 |    |   |
|    |/                  |    |   +
+    +----+----+----+----+    +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The Tray

824 T R C [p] 2 1

    +----+         +----+----+----+
   /    /|        /              /|
  +    + |       +----+         + |
 /    /  +----+--|   /         /  +
+----+  /        |  +----+----+   |
|    | +    +----+  |         |   |
|    |/    /|       |         |   +
+    +----+ |       +         +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

Left Offset

992 W O [p] 2

    +----+    +----+         +----+
   /    /|   /    /|        /    /|
  +    + |  +----+ |       +    + |
 /    /  +--|    | +----+-/    /  +
+----+  /   |    |/      +----+   |
|    | +    +    +----+  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

Left Finger

1024 Y Y [p2]

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +    +----+----+  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

The Y

Yellow: 52 x2, 256, 911, 928, 1024

52 D P [p]

    +----+         +----+----+----+
   /    /|        /              /|
  +    + |       +              + |
 /    /  +----+-/              /  +
+----+  /      +----+----+----+   |
|    | +       |              |   |
|    |/        |              |   +
+    +----+----+              +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The Side Tray

52 D P [p]

    +----+         +----+----+----+
   /    /|        /              /|
  +    + |       +              + |
 /    /  +----+-/              /  +
+----+  /      +----+----+----+   |
|    | +       |              |   |
|    |/        |              |   +
+    +----+----+              +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The Side Tray

256 J X B [p2] 3

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +                 |    |   |
|    |/                  |    |   +
+    +----+----+----+----+    +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The Tray

911 N C G 2

    +----+----+----+----+    +----+
   /                   /|   /    /|
  +         +----+----+ |  +    + |
 /         /|         | +-/    /  +
+----+----+ |         |/ +----+   |
|         | +         +  |    |   |
|         | |        /   |    |   +
+         + |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

Right Wall

928 V L D 2

    +----+    +----+----+    +----+
   /    /|   /         /|   /    /|
  +    + |  +----+----+ |  +    + |
 /    /  +--|         | +-/    /  +
+----+  /   |         |/ +----+   |
|    | +    +         +  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

The Tongue

1024 Y Y [p2]

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +    +----+----+  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

The Y

Green: 18, 52, 871, 928, 1024 x2

18 B B L [p] 2 0

    +----+    +----+----+----+----+
   /    /|   /                   /|
  +    + |  +                   + |
 /    /  +-/                   /  +
+----+  / +----+----+----+----+   |
|    | +  |                   |   |
|    |/   |                   |   +
+    +----+                   +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

Local Mail

52 D P [p]

    +----+         +----+----+----+
   /    /|        /              /|
  +    + |       +              + |
 /    /  +----+-/              /  +
+----+  /      +----+----+----+   |
|    | +       |              |   |
|    |/        |              |   +
+    +----+----+              +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The Side Tray

871 M T K 2 0

    +----+----+         +----+----+
   /         /|        /         /|
  +         + |       +         + |
 /         /  +----+-/         /  +
+----+----+  /      +----+----+   |
|         | +----+--|         |   |
|         | |       |         |   +
+         + |       +         +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

The Barbells

928 V L D 2

    +----+    +----+----+    +----+
   /    /|   /         /|   /    /|
  +    + |  +----+----+ |  +    + |
 /    /  +--|         | +-/    /  +
+----+  /   |         |/ +----+   |
|    | +    +         +  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

The Tongue

1024 Y Y [p2]

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +    +----+----+  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

The Y

1024 Y Y [p2]

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +    +----+----+  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

The Y

Orange: 1, 188, 871, 928, 1024 x2

1 A A [p]

    +----+----+----+----+----+----+
   /                             /|
  +                             + |
 /                             /  +
+----+----+----+----+----+----+   |
|                             |   |
|                             |   +
+                             +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The Key

188 I M [p]

    +----+         +----+    +----+
   /    /|        /    /|   /    /|
  +    + |       +    + |  +    + |
 /    /  +----+-/    /  +-/    /  +
+----+  /      +----+  / +----+   |
|    | +       |    | +  |    |   |
|    |/        |    |/   |    |   +
+    +----+----+    +----+    +  / 
|                             | +  
|                             |/   
+----+----+----+----+----+----+

The (Bottle) Opener

871 M T K 2 0

    +----+----+         +----+----+
   /         /|        /         /|
  +         + |       +         + |
 /         /  +----+-/         /  +
+----+----+  /      +----+----+   |
|         | +----+--|         |   |
|         | |       |         |   +
+         + |       +         +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

The Barbells

928 V L D 2

    +----+    +----+----+    +----+
   /    /|   /         /|   /    /|
  +    + |  +----+----+ |  +    + |
 /    /  +--|         | +-/    /  +
+----+  /   |         |/ +----+   |
|    | +    +         +  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

The Tongue

1024 Y Y [p2]

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +    +----+----+  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

The Y

1024 Y Y [p2]

    +----+                   +----+
   /    /|                  /    /|
  +    + |                 +    + |
 /    /  +----+----+----+-/    /  +
+----+  /                +----+   |
|    | +    +----+----+  |    |   |
|    |/    /|        /   |    |   +
+    +----+ |       +----+    +  / 
|         | +----+--|         | +  
|         |/        |         |/   
+----+----+         +----+----+

The Y

It seems natural to me to ask, "Can the given pieces be intermixed and used to make four other burrs simultaneously?" Sadly, I believe the answer is no.

The four original burrs are all solid and all the available pieces are in the "25 notchable" group. Obviously our four hypothetical alternative burrs would all still have to be solid (since if one was not, the remaining pieces would have too many cubies to form three more burrs). My Catalogue section lists all combinations of the "25 notchable" group that can form solid burrs. (Note that a given combination might assemble in more than one way, i.e. have multiple permutations, which is why my catalogue has fewer than 314 entries.) My Catalogue therefore contains all valid combinations of the available pieces that will form a solid burr - there are 21 of them and I list them in the table below. I highlight the four original burrs - we need to exclude them. Also note that there are only two remaining ways to use the two 871 pieces - in both cases they appear in a single burr - O or U, so only one of those must be in our hypothetical alternative set. Further, both of those choices also use the 824+992 pieces, so we can eliminate all other burrs that need those two pieces - which turn out to always appear together.

1
(x2) 18 52
(x3) 188
(x2) 256
(x2) 824 871
(x2) 911 928
(x3) 992 1024
(x6) NOTES
A 1 52 188 1024x3
B 1 52 256 928 1024x2
C 1 52 824 992 1024x2 uses 824+992
D 1 188x2 256 1024x2
E 1 188 256x2 928 1024x2
F 1 188 256 911 1024x2
G 1 188 256 824 992 1024 BLACK
H 1 188 871 928 1024x2 ORANGE
I 1 256x2 911 928 1024
J 1 256 824 911 992 1024 uses 824+992
K 18 52 256x2 928 1024
L 18 52 256 911 1024x2
M 18 52 256 824 992 1024 uses 824+992
N 18 52 871 928 1024x2 GREEN
O 18 824 871x2 992 1024 uses both 871
P 52x2 256x2 928x2
Q 52x2 256 911 928 1024 YELLOW
R 52x2 256 824 928 992 uses 824+992
S 52x2 824 911 992 1024 uses 824+992
T 52 256x2 911 1024x2
U 52 824 871x2 928 992 uses both 871

We have to use two 1 pieces and every non-eliminated burr containing 1 also uses at least one 256 except for burr A. The only way to use up two 1s but no 256s is to use two copies of burr A, but this burns all six 1024 pieces, which means to use the 871s we would have to choose U which requires no 1024. With Ax2 and U we have used 52x3 as well - but the only remaining burr that uses no 1024 is P, which requires 52x2. This means we cannot use Ax2 - we have to choose a 1 burr that also uses at least one 256, and that any non-1 burr that uses 256x2 can be eliminated! That eliminates K, P, and T.

Say we choose U to burn our 871x2. Now we have to use the single 18 piece, and we've got only one choice - burr L. Neither U nor L has used a 1 and we've used only a single 928 out of three - so both of the remaining two burrs have to use 1+928 (no remaining single burr uses 928x2), which eliminates A, leaving B, E, and I. However, with A eliminated, each 1 burr can use only a single 256 - which eliminates E and I leaving only B. We cannot duplicate B because U, L, and B each need a 52, using all three available and leaving none for the duplicate B. So we are left with no valid fourth burr.

OK, so we choose O to burn our 871x2. L is eliminated since we've used the single 18. We need to choose three more burrs, but the only burrs left all use 1 and we've only got two 1 pieces!

This set of 13 length-8 pieces is called Boite 13. The pieces are assigned letters A thru M, and correspond to our codes as follows:

A B C D H/E I/F J/G L/K M
1 52 103 256 792/911 824/975 888/1007 960/992 1024

They're all notchable. You don't get 188 or 928, and you only get one each of 256 and 1024. But you do get the less commonly supplied 888/1007 pair. According to BurrTools, there are only 13 distinct subsets of 6 that form solid burrs - I have included those 13 in my catalog, and identified them as B13S.n where n goes from 1 to 13. These pieces can form 9104 burrs allowing internal holes. The highest level is 4. I didn't find any of the holey examples I tried particularly compelling - if I include them in the catalog, I'll label them as B13H.n.

Colin Gaughran is a woodworker in Connecticut. Colin can make any burr pieces, notchable, millable, or even general, using his CNC machine. Colin has (so far) made 36 burr pieces for me, including: 3, 52, 103 (x2), 160, 188, 256, 359/615, 448/736, 463, 499, 508, 512/768, 742, 743, 792, 824 (x2), 832, 871, 880, 888, 911, 926, 928, 943, 960/992, 975, 1007, 1015, 1024, and a 1024 with a rounded center cross-bar. These pieces can be used to make many interesting burrs, including Bill Cutler's #306, CINTVY, FILTVY, and FGINOY.

Here is Rob's Burr No. 1, which has 3 solutions - one at level 3, and two at level 9:

{ 499, 736, 768, 943, 992, 1015 }
As far as I know, this is the first time this particular burr has been made!

Aaron Siegel kindly 3D printed the set of pieces to construct Rob's Burr No. 1. Aaron has devised a coloring scheme such that in one Level-9 solution each pair of like-colored pieces are parallel, in the other Level-9 solution one pair of colors are swapped, and in the Level-3 solution a different pair is swapped.

Rob's Burr No. 1 - coloring by Aaron Siegel

Thanks, Aaron!

Wayne Daniel (Interlocking Puzzles) made this nice set of 42 of the notchable pieces which can be used to make 314 solid burrs. I believe the pieces are made of of Mahogany wood, with a Walnut box. Each piece is 0.75" square and 2.5" long, so his unit cube is 3/8 inches on an edge, and these are "length 6." The set includes a series of cards listing the six-tuples of each of the 314 burrs, and giving assembly hints by telling the adjacent pairings.

Unfortunately, I have found that certain holey burrs that are constructible from the notchable set, cannot be made to work using Daniel's set - his esthetic beveled treatment of the ends of the pieces, while fine for the 314 solid burrs, prevents certain necessary movements when trying the holey burrs. In particular, designs which use the "jutting jaw" technique as in the JVK 25.1 design, don't open far enough to allow the 3/8" cubie of a piece to pass through.

Pentangle offered a nice boxed set of the same 42 pieces. Unlike the IP set which has length 6 pieces, the Pentangle pieces are length 8.

Interlocking Puzzles also offered another nice boxed set, of 35 pieces - called the Level 5 Set. Another collector, Jim Storer, shows both the IP 42-piece set I have here, and the IP Level-5 35-piece set on his website.

I finally managed to find the lovely Chinese Cross Compendium issued by Pentangle.

A Level-5 Burr Set in mahogany and plane woods, made by Jack Krijnen. The attention to detail is superb! This set provides 35 (42 including duplicates) out of the 837 possible traditional six-piece burr pieces, at length 6. (The same as in a similar set made by Interlocking Puzzles ca. 2000, shown on Jim Storer's site. The piece numbering employed by Krijnen, David Winkler's scheme, is also identical to that used for the IP set.) The particular pieces are all notchable, and are those needed to build level-5 burrs. The set includes a small pair of wooden tweezers with which one can extract pieces from the box. The box is about 118mm x 90mm. The pieces measure 3x1x1 cm.

Caramel Case Burr Set - designed and made by Jerry McFarland
from Wenge, Walnut, Cherry, Acrylic, magnets, and Maple plywood.
I got serial number 3!
This contains the standard 42-piece set used to make 314 solid burrs
but because of the dimensional compliance of the pieces,
many many additional holey burrs can be made!
The pieces are engraved using the von Känel numbering system I advocate,
so it is quite easy to pull a needed selection from the beautiful case.
Doesn't it look like a box of fine Caramel candies? Jerry's wife thought it did, hence its name.
Also engraved on each piece is its "standard" letter ID as used in Pentangle's set from the 1980's
and the number of copies of the piece in the 42-piece set.
I love how the pieces are spaciously arranged and easy to extract or replace.
The acrylic top and unusual magnetic-closure Wenge edges are very elegant.
The tolerances in the case are so good that replaced pieces simply float down into place on a cushion of air!

Penultimate Burr Set - with a trick opening box, made by Eric Fuller
from Ash and Cherry woods.
It isn't as if I need another burr set...

DDD Burr Set aka "Darryl's Dense Dozen" - in brass, selection by Darryl Adams,
burrs machined by Bryan Turner, produced by and purchased from CubicDissection.
The burr pieces have 6mm voxels, and are standard 2x2x6 prisms, so measure 12x12x36mm.

The 12 pieces included are:

A B C D E F G H I J K L
1 188 256 975 1007 792 824 888 928 992 960 1024

The inside lid lists a set of ten puzzles. With this piece set, Darryl says there are 530 possible puzzles (many of which are uninteresting), 24 of which are solid, and 42 puzzles with unique solutions. 2 through 6 had already appeared in my list. 7 through 10 do not use the key piece. Using this set, 7 is the only 3-hole puzzle with a unique solution - it fits together in two 3-piece halves. Using this set, 10 is the only level 2 with a unique solution. The CubicDissection page links to a PDF giving more information.

Bryan has machined a set of all 59 notchable pieces and posted a photo I really like
where they are arranged as in my burr piece tables:

Notchables - Turner

Other burr puzzle sets:

The Ultimate Burr Set - Creative Crafthouse

Creative Craft House offers the Ultimate Burr Set that includes 27 pieces and can make over 60 puzzles. Thanks, Dave!
Ken Irvine wrote up a nice article about this set, which he has given me permission to mirror so you can download a copy.

Philos offers their set #6025, called "151er Teufel" having 20 pieces and making 159 puzzles
(I don't have this.)
Check Amazon.de

Here are the pieces included:

Teufel Piece	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
My ID	1024	1024	960	992	928	888	1007	824	824	975	975	792	911	256	188	52	52	18	18	1

Omitted: { 35, 103, 120, 86, 154, 871, 359/615, 856/943 }

This is the Onietoiy 20pcs DIY Puzzle - a burr set from Onietoiy.

The set includes 16 traditional burr pieces of length 8, and four special pieces of length 16 which are used to assemble multi-burr constructs.
The instructions give 19 traditional 6-piece burrs which use the key piece, and 4 which use 52 rather than the key piece,
as well as several interesting larger structures to be made with the special long pieces.

The pieces are identified with a strange numbering scheme - I map to my IDs in the table below:

Onietoiy ID	My ID
0	1
0033	52 - half tray
3033	188 - can opener
1133	208 - half tray with wall on left vs 64 (right) not incl
3333	256 - full tray
3053	670 - (L in middle, open right) vs 412
3373	768 - (tray w/ gap tooth on right)
0335	792 - wall left gap
0375	824 - left offset
0775	888 - club left gap (no right club 1007)
033A	911 - wall right gap
3553	928 - tongue
03BA	975 - right offset
1573	976 - pc from G4/Marseille
3773	1024
3773	1024

Historically Catalogued Burrs

Arthur L. Smith was a noted puzzle expert in the early 1900's - he wrote an article on burr puzzles published in the March 1926 issue of Popular Science magazine. Here is a link to the Google Books page.

Smith's pieces and his recommended counts:

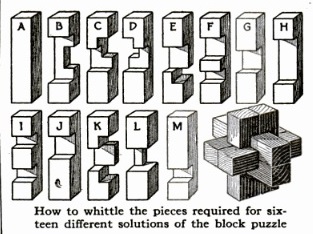
Smith ID A B C D E F G H I J K L M
My ID 1 1024 824 975 911 188 103 256 154 52 928 871 18
Count 1 3 1 1 1 2 1 2 1 2 1 1 1

Smith's diagrams are very clear and there is no mistaking the identities of the pieces.
All of Smith's pieces are among the 25 notchables used in solid burrs.

Smith describes 16 burrs that can be constructed from this set.

Here are Smith's 16 sets in our terminology. W# indicates the same burr is given by Wyatt, F# indicates the same burr is given by Filipiak.

1. { 1, 911, 824/975, 1024x2 } W2
2. { 1, 103, 188, 1024x3 } F45
3. { 1, 52, 188, 1024x3 } W3, F4
4. { 1, 154, 256x2, 1024x2 } W5, F12
5. { 1, 52, 256, 928, 1024x2 } W6, F2
6. { 1, 154, 871, 1024x3 } W7, F42
7. { 1, 103, 256, 928, 1024x2 } W8, F28
8. { 1, 188, 256x2, 928, 1024 } F15
9. { 1, 188x2, 256 1024x2 } F24
10. { 52x2, 103, 928, 1024x2 } close to W9, F64 but both mistakenly substitute 871 instead of the correct 928.
I believe this is evidence that Wyatt cribbed from Smith! Wyatt's pieces are the same set as Smith's but lettered slightly differently, and his 'K' is 871, whereas Smith's 'K' is 928.
11. { 18, 52, 256, 911, 1024x2 } W10, F66
12. { 1, 52, 975, 1024x3 } W11
13. { 1, 188, 256x2, 1024x2 } W4, W12, F14
14. { 1, 52, 256, 1024x3 } W13, F1
15. { 1, 188, 256, 975, 1024x2 } W14
16. { 52, [154 or 188], 256, 911, 1024x2 } close to W15, F65 but both mistakenly substitute an extra 256 for the second 1024.
More evidence that Wyatt cribbed from Smith. In Wyatt's slightly different lettering, he assigns 'B' to 256, whereas Smith's 'B' is 1024. Note Smith's description of the last few steps in assembling this puzzle: "then B and I or F (no key block)." Compare with Wyatt's: "and B and I or F (no key)." Seems to me like Wyatt inadvertently copied this and failed to perform the necessary substitution to account for his relettering, where the needed 1024 is not 'B' but 'F.' Wyatt should have said: "and F and I or M."

In my table of puzzles below, I will highlight Smith's burrs like this.

Smith wrote several other articles on puzzles for Popular Science:

On peg solitaire puzzles in the May 1926 issue.
On sliding piece puzzles in the July 1926 issue.
On the "Stomachion of Archimedes" in the November 1926 issue.
On "A Square Peg in a Round Hole" in the July 1927 issue.
On an interlocking cube in the Sept 1927 issue.
On an interlocking puzzle box (trick bank) in the July 1931 issue.
On a dovetail puzzle joint in the Nov 1931 issue, and the Mar 1932 issue.
On the 5x5 Magic Square in the Feb 1932 issue.
On a "new form of the Chinese Cross puzzle" in the May 1932 issue.
On a square dissection in the Nov 1932 issue.

The book Puzzles in Wood, written by Edwin M. Wyatt, was published in 1928 by the Bruce Publishing Company. I have a copy of the fourth printing from 1939. Wyatt includes a section on the six piece burr, shows clear plans for 13 pieces he labels A through M, and gives a list of six-piece sets for 15 puzzles.
In the list below, Wyatt's puzzles are highlighted like this.

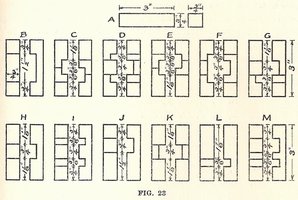
Wyatt's Pieces
They correspond to:

A	B	C	D	E	F	G	H	I	J	K	L	M
1	256	824	928	975	1024	911	103	154	52	871	18	188

all of which are notchable.

Wyatt's Puzzles

Filipiak book The book 100 Puzzles - How to Make and Solve Them, written by Anthony S. Filipiak, was published in 1942 by A. S. Barnes and Company. In his book, Filipiak includes a section on the "Six Piece Burr Puzzle," beginning on page 79. He says that though he has over a thousand mechanical and manipulative puzzles in his collection, his favorite puzzle is the six piece burr.

He gives diagrams for 38 burr pieces, and lists his "prize collection" of 73 burr puzzles using those pieces, "collected the world over by correspondence, travel, and research into ancient books of magic, tricks, games, and puzzles." He admits "no doubt there are a few more to be added."

I have not reproduced all 73 designs here, but I highlight Filipiak designs like this.

Several of the designs in his list of 73 puzzles, when I checked using Jurg's applet, have no solution - maybe the wrong pieces were listed, or as noted below, the actual configuration of the pieces themselves are open to interpretation. Or, perhaps Filipiak himself hadn't bothered to actually construct all of the designs - but that seems unlikely given his enthusiasm. I cannot imagine that his editor could have checked the work, however! NOTE - see info on Smith, above - I believe Filipiak copied from Wyatt, who mis-copied from Smith - this explains some of the errors.

Filipiak's pieces correspond to:

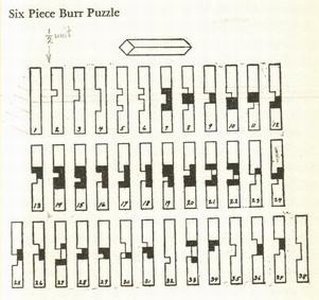
1	2	3	4	5	6	7	8	9	10
1	18	52	256	154	188	1024	928	871	911? (463?)
11	12	13	14	15	16	17	18	19	20
792	975	824	512	768	1016	1023	1015	760	511
21	22	23	24	25	26	27	28	29	30
992	960	564?	788	820	973	927	359	615	461?
31	32	33	34	35	36	37	38
909	35?	920	20	103	1007	888	120

Filipiak's notes seem to contain several errors: his pieces #2 and #32 appear to be duplicates of what I call #18, although his #32 might be my #35; his #10 as drawn equals my #463, but that interpretation results in several of Filipiak's designs having no solution - from its position in his list it might be a mistaken drawing of my #911, the complement to its neighbor #11 which is my #792.

Filipiak missed pieces #35 and #86, but there are only 3 uses of #35 among the 314 solid burrs, and few of #86. He also missed the pair 856/943, but neither of those are used often, either.

All of the pieces in his set highlighted like this are used in only 6 of his burrs!
The mirror pair 512/768 is used only once, in his burr #63.

In August 2017, I found the following on auction - it appeared to me to be a set of burr pieces, but the seller had assumed that the entire set would be used to construct one large puzzle - no documentation was included. The pieces bear hand-pencilled numbers on their ends, ranging from 1 to 38, and there are 90 pieces. Once I received the set, took inventory, and examined the piece shapes and numbering, it became evident that this is in fact a set of Filipiak's pieces, using his numbering scheme. I wonder who made them, following Filipiak's instructions? Whoever it was did a pretty accurate job.

There are only a few discrepancies:

piece #18 is supposed to map to ID 1015, but is instead a copy of piece #9 which equals ID 871 (barbells)
The two copies of piece #10 should map to ID 911, but they are offset so actually are 463 - this faithfully follows the error in Filipiak
piece #24 is supposed to be 788, but is instead 280 which does not match the Filipiak diagram.
piece #32 is the same as #2 - both map to 18 local mail
the only copy of piece #35 (103 - the half tray) has a notch that is a bit too tight
piece #37 should be 888, the mirror to piece #36 which is 1007 - but its notch is offset so it is not 888.

The seller obtained the set at a flea market in Virginia but unfortunately could say nothing else of its provenance. They were supplied in a crude oblong cardboard box, shown first above - I fashioned a slightly less crude and more convenient cardboard container for the set, with internal separators, shown next. The pieces appear to be made from walnut. Each piece has a 1/2" square cross section and is 3" long, and notches are 1/4" so these are length-12.

I am able to construct many burrs using this set, including the complexly-notched Tenyo Brother, since in effect a 463 is supplied. Sadly, however, due to the flaws mentioned above, there are several among Filipiak's 73 burrs that cannot be constructed using this set.

Still, it is cool to have come into possession of some past puzzler's treasure - it must have taken quite some effort to craft all these pieces - chisel marks can be seen in the finely carved notches. I wonder how many other readers of Filipiak's book actually went to the trouble to make the set of burr pieces for which he evinced so much enthusiasm?

My Catalogue of Burrs to Try

This section gives a list of burrs to try once you have a set (or can make your own pieces, for example from LiveCube or Lego). I've included solid and holey designs. There are several sources that give the full list of all 314 solid burrs that can be produced with the set of 42 notchable pieces, including Slocum and Botermans' 1987 Puzzles Old and New. That list of 314 puzzles contains multiple entries for a set of six pieces when that set can go together in different ways, so there are not actually 314 unique six-piece sets. I have folded all the sets represented by those 314 puzzles into my list. I have tried to catalogue interesting puzzles I've run across and give their names or designers when I know them.

The catalog below is ordered by piece number - with the six pieces sorted by number, lowest first. Mirror pair pieces are listed together. I have color-coded the pieces per my guide tables above, to try to make it easier to see how the designs may be related.

In the notes accompanying the puzzles I have used various colors to highlight particular puzzles as follows...

Pieces highlighted in this color are from the table of additional pieces. If a burr's piece list does not contain any pieces highlighted like this, then it (most likely) can be constructed using the set of 42 notchable pieces.

The pieces 512/768 are used frequently and are specially highlighted.

The four common designs

Among the oldest documented

The 16 designs from Arthur L. Smith's March 1926 Popular Science article

The 15 burrs described by Edwin Wyatt in his 1928 Puzzles in Wood

In Filipiak's 1942 book

Can be made with the Professor/Professional Puzzle set

The "Fearsome Four"

Stewart Coffin's three designs

Some of Bill Cutler's designs
(Bill gives lists of "holey" burr designs, and other burr designs on his site.)

Mentioned on Bruno Curfs' site
Ranked easiest by Curfs
You might use these to introduce a beginner or a child to this category. Incidentally, Curfs, Coffin, and Cutler rate Cutler's #306 as the most difficult of the notchable solid burrs.

Jurg von Kanel designs

Peter Roesler's designs

David Winkler's designs

Keiichiro Ishino's designs
Ishino offers extensive analysis of the six-piece burr (as well as many other puzzles), giving catalogues of pieces and of designs. He lists many of the puzzles listed here, too.

Anyway, herewith my list, also "collected the world over!"

(Note that the ordinal list entry numbers will change if/when I modify the list, so you should not rely on them as identifiers for given burr puzzles. They're just there to provide a count of the number of entries in my list.)

1, 52, 188, 1024 x3
- Smith #3, Wyatt #3, Filipiak #4
1, 52, 256, 928, 1024 x2
- Smith #5, Wyatt #6, Filipiak #2 ; also U.S. Patent 1425107 - Levinson 1922. May be the earliest known burr, depicted in a 1755 book by Pablo Minguet y Irol (b. 1700 d. ca. 1775). Appeared as the "Small Devil's Hoof" in a 1785 catalogue.

1, 52, 256, 960/992, 1024
- Filipiak #3 (corrected) - substituting 824 for 992, as given in Filipiak, won't work; B13S.1
1, 52, 256, 1024 x3
- Smith #14, Wyatt #13, Filipiak #1
1, 52, 824, 992, 1024 x2
- Filipiak #7 - the mirror of his #6. Professional Puzzle set #3
1, 52, 824, 1024 x3
- Filipiak #5 - 1 solution; compare to Wyatt #11
1, 52, 888 or 1007, 928, 1024 x2
- 1 soln.
1, 52, 888 or 1007, 960/992, 1024
- Filipiak #10 (use 1007), Filipiak #11 (use 888) - 2 solutions each. B13S.2
1, 52, 960, 975, 1024 x2
- Filipiak #6 - an improvement on Wyatt #11, substituting 960 for a 1024 and thereby eliminating the single void.
1, 52, 975, 1024 x3
- Smith #12, Wyatt #11

1, 86, 871, 1024 x3
- the only use of piece #86 with the key #1 - requires piece #871 - easy

1, 103, 188, 1024 x3
- Smith #2, Filipiak #45; An "anomaly" with "inside" cubies showing
1, 103, 256, 928, 1024 x2
- Smith #7, Wyatt #8, Filipiak #28, "Chinese Puzzle E"
1, 103, 256, 960/992, 1024
- Filipiak #37 - 3 solutions; B13S.3
1, 103, 824, 992, 1024 x2
- 3 solns.
1, 103, 824, 1024 x3
- See above - using 992 instead of a third 1024 eliminates the single internal void here.
1, 103, 888 or 1007, 928, 1024 x2
- 1 soln.
1, 103, 888 or 1007, 960/992, 1024
- B13S.4 (1007)
1, 103, 960, 975, 1024 x2
- Filipiak #51 - 3 solns.

1, 120, 188, 960/992, 1024
- Filipiak #47 - 1 solution
1, 120, 256, 928 x2, 1024
- 1 soln. - I found this tricky for some reason.
1, 120, 256, 928, 960/992
- 3 solns.
1, 120, 792 or 911, 928, 1024 x2
- 1 soln.
1, 120, 792 or 911, 960/992, 1024
- 2 solns.
1, 120, 856, 928, 960, 1024
- 2 solns.
1, 120, 856, 960 x2, 992
- 1 soln.
1, 120, 871, 928, 1024 x2
- Filipiak #48 - 1 solution
1, 120, 871, 960/992, 1024
- 3 solns.
1, 120, 928, 943, 992, 1024
- 2 solns.
1, 120, 943, 960, 992 x2
- 1 soln.
1, 128, 188, 512, 960/992
- from Peter Kaldeway's site
1, 128, 512, 792, 928, 1024
- Soviet Hedgehog

1, 154, 256 x2, 1024 x2
- Smith #4, Wyatt #5, Filipiak #12, Professional Puzzle set #1. This one is very easy (BC #2). Any burr using 2x1024 is easier than most - adding 2x256 makes it somewhat trivial. "The Puzzle of Puzzles" - made in Japan; See plans for Betelgeuse at www.craftsmanspace.com; The Double-Cross Puzzle, issued by the General Engineering & Design Co. of Detroit, Michigan.

1, 154, 256, 888 or 1007, 1024 x2
- Filipiak #22 (corrected, use 888 not 103 as listed), Filipiak #23 (use 1007)
1, 154, 871, 1024 x3
- Smith #6, Wyatt #7, Filipiak #42

1, 188 x2, 256, 1024 x2
- Smith #9, Filipiak #24; also Coirligheile ("Gaelic Whorl") or a Ghlasmhahaidh ("lock of scoffing"), from The Games & Diversions of Argyleshire published in 1901. See diagram on p. 17 of the PDF and text on page 192 by the document's numbering. On display at the Pitt Rivers Museum - article and photo at Meople's Magazine, 22 Oct 2010.

1, 188, 256 x2, 928, 1024
- Smith #8, Filipiak #15
1, 188, 256 x2, 960/992
- Filipiak #16
1, 188, 256 x2, 1024 x2
- Smith #13, Wyatt #4 (also #12), Filipiak #14, can be made with the Professor set
1, 188, 256, 512, 832, 992
- (solid) Yamanaka "Shap" 3505 set, No. 4
1, 188, 256, 792 or 911, 1024 x2
- (solid) Kitajima #1 (use 911)
1, 188, 256, 824, 992, 1024
- Filipiak #27, Yamanaka Black set, can be made with the Professor set - 2 solns. - mirror of Hoffmann below
1, 188, 256, 824, 1024 x2
- Filipiak #25; compare to Wyatt #14; can be made with the Professor set (1 unnecessary hole)
1, 188, 256, 888 or 1007, 928, 1024
- 1 soln.
1, 188, 256, 888 or 1007, 960/992
- 1 soln.
1, 188, 256, 960, 975, 1024
- Filipiak #26; Described in Hoffmann's 1893 Puzzles Old and New Chapter III as No. XXXVI "The Nut (or Six-piece) Puzzle"; also sold as the "Burr Puzzle" by Toys From Times Past.

1, 188, 256, 975, 1024 x2
- Smith #15, Wyatt #14, can be made with the Professor set

1, 188, 512, 576, 976, 1024
- "Dreveny Kriz II"
1, 188, 512, 824, 992, 1023
- Teufelsknoten Schlüsselanhänger
1, 188, 512, 832, 975, 1024
- Devil's Knot, G4, Tommerknude, "Chinese Puzzle B"
1, 188, 768, 824, 976, 1024
- HABA Teufelsknoten; Puzzlemaster.ca Enigma; also known as "Notched Sticks." The pieces are kind of the "mirror image" of the Devil's Knot above - pick either the left or right of each of the three twins: 512/768, 832/976, and 975/824. I have seen this called "The Cross of Marseille." Also see plans for Cassiopeia at www.craftsmanspace.com.

1, 188, 792, 888, 1024 x2
- (solid) 1 soln.
1, 188, 824, 888 or 1007, 992, 1024
- (solid) 1 soln.
1, 188, 824/975, 1024 x2
- The Yamato Block Puzzle, Filipiak #44, Professional Puzzle set #2. Easy. Also appeared as the "Locked Cross" from New Zealand. Also see U.S. Patent 1350039 - Senyk 1920. Louis Vuitton Le Pateki puzzle (maple, sycamore).

1, 188, 871, 928, 1024 x2
- Filipiak #43, Yamanaka Orange set
1, 188, 871, 960/992, 1024
- Filipiak #46 - 3 solutions
1, 188, 888 or 1007, 960, 975, 1024
- (solid) 1 soln.
1, 188, 911, 1007, 1024 x2
- (solid) 1 soln.
1, 208, 256, 670, 1024 x2
- Tang Yunzhou. Zhongwai xifa tu shuo: e huan huibian (Chinese and Western magic with diagrams: compilation of magic) - Shanghai, 1889

1, 256 x3, 928 x2
- The Diabolical Structure - possibly the easiest (BC #1). Filipiak #13
1, 256 x2, 792 or 911, 928, 1024
- Filipiak #17 (use 911) and Filipiak #18 (use 792)
1, 256 x2, 792 or 911, 960/992
- Filipiak #20 (use 911) and Filipiak #21 (use 792) - compare to Filipiak #17/18 and note how the 928+1024 pair replaces the 960/992 pair.
1, 256, 792 x2 or 911 x2, 1024 x2
- Filipiak #30 (use 792) and Filipiak #31 (use 911) - 1 soln.
1, 256, 792 or 911, 824, 992, 1024
- B13S.6 (use 911) - 1 soln.
[[ 1, 256, 792 or 911, 975, 992, 1024]]
- Filipiak #32 (911) and Filipiak #33 (792) - BOTH no soln. - compare w/ B13S.6 & 7
1, 256, 792, 928, 1007, 1024
- vintage small brown wooden burr I got from England; see plans for Andromeda at www.craftsmanspace.com, where you can find several puzzle plans for woodworkers.
1, 256, 792 or 911, 960, 975, 1024
- B13S.7 (use 911) - the "mirror image" of B13S.6
1, 256, 792, 960/992, 1007
- 1 soln.
1, 256, 820, 928, 1007, 1024
- Interlocking keychain puzzle burr from France. 1 soln.
1, 256, 824 x2, 992 x2
- 1 soln.
1, 256, 824/975, 928, 1024
- Ivory Chinese Cross; Wyatt #1, Filipiak #29; "Chinese Puzzle G"; Bell's Maltese Cross keychain; Russian "Admiral Makarov's Puzzle"; Misfit - advertising Phenyo-Caffein; "The Chinese Cross" in The Boy's Own Toymaker by Landells 1859, and in the 1857 Magician's Own Book; see U.S. Patent 1388710 - Hime 1921, for these on a string.

1, 256, 824, 928, 992, 1007
- mirror of "Chinese Star"
1, 256, 824/975, 960/992
- Filipiak #41 - 2 solutions; B13S.5
1, 256, 888, 911, 928, 1024
- 1 soln.
1, 256, 888, 911, 960/992
- B13S.8
1, 256, 888, 928, 960, 975
- Saw this as the "Chinese Star."
1, 256, 888/1007, 928, 1024
- Triple Cross
[[1, 256, 928, 960, 975, 1007]]
- Filipiak #38; no soln for this set, but compare to the "Chinese Star"
1, 256, 960 x2, 975 x2
- 1 soln.

1, 359, 824, 928, 1024 x2
- 1 soln.
1, 359, 824, 960/992, 1024
- 2 solns.
1, 359, 888, 928, 960, 1024
- A tricky solid burr I like
1, 359, 888, 960 x2, 992
- 1 soln.

1, 464, 768, 800, 832, 1024
- Brown's Burr - See U.S. Patent 1225760 - Brown 1917.
1, 615, 928, 975, 1024 x2
- 1 soln.
1, 615, 928, 992, 1007, 1024
- mirror of the tricky solid burr I like
1, 615, 960/992, 975, 1024
- 2 solns.
1, 615, 960, 992 x2, 1007
- 1 soln.
1, 792 x2, 1007, 1024 x2
- 1 soln.
1, 792 or 911, 824/975, 1024 x2
- Smith #1 (use 911), "Chinese Puzzle F" (use 792), Wyatt #2 (use 911), Filipiak #49, if his #10 = 911, Filipiak #50 (use 792)
1, 792, 824, 992, 1007, 1024
- mirror of B13S.11 - 2 solns.
1, 792, 856, 960, 1007, 1024
- 1 soln.
1, 792, 888, 960, 975, 1024
- 1 soln.
1, 824 x2, 975, 992, 1024
- 2 solns.
1, 824, 856, 871, 1024 x2
- 1 soln.
1, 824, 856, 960/992, 1007
- 1 soln.
1, 824, 871, 888, 992, 1024
- 2 solns.
1, 824/975, 888 or 1007, 928, 1024
- 1 soln.
1, 824/975, 888 or 1007, 960/992
- B13S.9 (use 888)
1, 824, 911, 992, 1007, 1024
- B13S.10
1, 824, 960, 975 x2, 1024
- 2 solns.
1, 856, 871, 888, 960, 1024
- 1 soln.
1, 871, 888 x2 or 1007 x2, 928, 1024
- 1 soln.
1, 871, 888 x2 or 1007 x2, 960/992
- 1 soln.
1, 871, 943, 975, 1024 x2
- 1 soln.
1, 871, 943, 992, 1007, 1024
- 1 soln.
1, 871, 960, 975, 1007, 1024
- 2 solns.
1, 888, 911 x2, 1024 x2
- 1 soln.
1, 888, 911, 943, 992, 1024
- 1 soln.
1, 888, 911, 960, 975, 1024
- B13S.11
1, 888, 943, 960/992, 975
- 1 soln.

18 x2, 256 x2, 1024 x2
- The 3rd easiest burr (BC #3).
18 x2, 256, 888 or 1007, 1024 x2
- compare to BC#3 - substitute either 888 or 1007 for one 256
18 x2, 512/768, 1015, 1024
- Filipiak #63 - 1 solution
18 x2, 871, 1024 x3
- contrast with 18,35 below - this shows how 871 can be placed with its crossbar outboard (w/ 18) or inboard (w/ 35)
18 x2, 888/1007, 1024 x2
- nice symmetry
18, 35, 871, 1024 x3
- one of only 3 uses of piece #35 among the 314 solid burrs.
18, 52, 103, 1024 x3
- easy
18, 52, 188, 888 or 1007, 1024 x2
- use 888 or 1007
18, 52, 256 x2, 928, 1024
- 4 apparent assemblies but only 1 solution. Not too tough.
18, 52, 256, 792 or 911, 1024 x2
- Smith #11 (use 911), Wyatt #10 (911), Filipiak #66, if his #10 = 911
18, 52, 256, 824, 992, 1024
- Professional Puzzle set #4
18, 52, 256, 888 or 1007, 928, 1024
- use 888 or 1007
18, 52, 256, 888 or 1007, 960/992
- use 888 or 1007
18, 52, 256, 960, 975, 1024
- mirror of Professional Puzzle set #4
18, 52, 792, 1007, 1024 x2
- 3 solns. 18+1024, 18+1007 (2 ways)
18, 52, 824/975, 1024 x2
- 18+1024 key, 2 solns.
18, 52, 824, 992, 1007, 1024
- 4 solns.
18, 52, 856, 960, 1007, 1024
- one of the more interesting solid assemblies featuring an 18+1024 "key" - 1 soln.
18, 52, 871, 928, 1024 x2
- Yamanaka Green set
18, 52, 871, 960/992, 1024
- 3 solns. - all use 18+871 key - compare w/ 18,86 below
18, 52, 888, 911, 1024 x2
- 3 solns. 18+1024, 18+888 (2 ways)
18, 52, 888, 943, 992, 1024
- mirror image of "interesting" one above - 1 soln.
18, 52, 888, 960, 975, 1024
- 4 solns.
18, 86, 871, 960/992, 1024
- one of only two uses of piece #86 without the key #1 among the 314 solid burrs.
18, 103, 120, 960/992, 1024
- 1 soln.
18, 103, 824/975, 1024 x2
- 2 solns.
18, 103, 824, 992, 1007, 1024
- 1 soln.
18, 103, 871, 960/992, 1024
- compare w/ 18,86 above
18, 103, 888, 960, 975, 1024
- 1 soln.

18, 120, 188 x2, 1024 x2
- 1 soln.
18, 120, 188, 824, 992, 1024
- 1 soln.
18, 120, 188, 960, 975, 1024
- 1 soln.
18, 188, 824/975, 888 or 1007, 1024
- 1 soln.
18, 256, 792 or 911, 824/975, 1024
- 2 solns.
18, 359, 824, 871, 1024 x2
- 1 soln.
18, 359, 824, 911, 1024 x2
- 1 soln.
18, 359, 824, 943, 992, 1024
- 1 soln.
18, 615, 792, 975, 1024 x2
- 1 soln.
18, 615, 856, 960, 975, 1024
- 1 soln.
18, 615, 871, 975, 1024 x2
- 1 soln.
18, 792, 824/975, 1007, 1024
- 2 solns.
18, 824 x2, 975, 992, 1007
- 1 soln.
18, 824, 871 x2, 992, 1024
- 1 soln.
18, 824/975, 888, 911, 1024
- 2 solns.
18, 824, 888, 960, 975 x2
- 1 soln.
18, 871 x2, 960, 975, 1024
- two 871s! - 1 soln.

20, 52, 824, 911, 1024 x2
- Filipiak #67 - his only use of his piece #34 / my #20.
35, 52, 871, 928, 1024 x2
- the second of only 3 uses of piece #35 among the 314 solid burrs.
35, 52, 871, 960/992, 1024
- the third of only 3 uses of piece #35 among the 314 solid burrs, this set goes together 3 ways.
35, 359, 960/992, 975, 1024
- EFNOQY discussed by Bruno Curfs
35, 975, 992 x2, 1024 x2
- EOOQYY - Simple Lock

[[ 52 x2, 103, 871, 1024 x2]]
- Wyatt #9, Filipiak #64 - NOTE - this set doesn't work - it has too many interior cubes. Why did they both include it?
52 x2, 103, 928, 1024 x2
- Smith #10 - The answer to the question above - because Wyatt cribbed incorrectly from Smith!
Also, a large solid burr I played with at George Hart's house.
52 x2, 103, 960/992, 1024
- (solid) 3 solns.
52 x2, 188, 888 or 1007, 928, 1024
- (solid) 1 soln.
52 x2, 256 x2, 928 x2
- Another very easy burr - BC #4
52 x2, 256, 792 or 911, 928, 1024
- Yamanaka Yellow set (911)
52 x2, 256, 792 or 911, 960/992
- 1 soln.
52 x2, 256, 824, 928, 992
- 1 soln.
52 x2, 256, 928, 960, 975
- 1 soln.
52 x2, 792/911, 1024 x2
- 3 solns.
52 x2, 792, 928, 1007, 1024
- 1 soln.
52 x2, 792, 960, 975, 1024
- 3 solns.
52 x2, 792, 960/992, 1007
- 1 soln.
52 x2, 824, 911, 992, 1024
- 3 solns.
52 x2, 824/975, 928, 1024
- 2 solns.
52 x2, 824, 928, 992, 1007
- 1 soln.
52 x2, 824/975, 960/992
- symmetric halves, no holes - contrast with B13S.12, which I think is harder
52 x2, 824, 928, 992, 1007
- 1 soln.
52 x2, 856, 928, 960, 1007
- 1 soln.
52 x2, 888, 911, 928, 1024
- 1 soln.
52 x2, 888, 911, 960/992
- 1 soln.
52 x2, 888, 928, 943, 992
- 1 soln.
52 x2, 888, 928, 960, 975
- 1 soln.

52, 56, 792, 975, 928, 1024
- "Chinese Puzzle C" (3 solns.)
52, 86, 871, 928, 960/992
- the 2nd of only two uses of piece #86 without the key #1 among the 314 solid burrs.
52, 88, 768, 888, 992, 1024
- Bill Cutler's BB31-10-40 - the least un-notchable 1-hole level 3
52, 103, 120, 928, 960/992
- Kitajima #2 (no holes)
52, 103, 824/975, 928, 1024
- 2 solns.
52, 103, 824, 928, 992, 1007
- 1 soln.
52, 103, 824/975, 960/992
- B13S.12 (no holes)
52, 103, 871, 928, 960/992
- LNOPST - 3 assemblies, 1 solution; Bruno Curfs rates this 5th hardest among the solid notchables. Not too hard once you recognize it has (a) the L&P (52,928) "key," (b) typical symmetric arrangement of N&O (960/992), and (c) T 871 used in its "inside out" mode.
52, 103, 888, 928, 960, 975
- 1 soln.
52, 120, 188 x2, 928, 1024
- 1 soln.
52, 120, 188, 824, 928, 992
- 1 soln.
52, 120, 188, 928, 960, 975
- 1 soln. (mirror of above)
[[ 52, 154, 256 x2, 911, 1024]]
- Filipiak #65, Wyatt #15(a) - no solution even if Filipiak's #10 is 463
52, 154 or 188, 256, 911, 1024 x2
- Smith's #16 - what Wyatt #15(a) meant to be.
52, 188, 615 (or 103), 928, 1007, 1024 (with rounded crossbeam)
- "Twisting Key Burr" from Wish. 3 solns.
52, 188, 824/975, 888 or 1007, 928
- 1 soln.
52, 256 x2, 911, 1024 x2
- Wyatt #15(b) - 7 solutions
52, 256, 792 or 911, 824/975, 928
- 2 solns.
52, 256, 888/1007, 1024 x2
- Jurg von Kanel's Burr in a Cube - assemble this inside a cubic cage.
52, 359, 824, {871 or 911}, 928, 1024
- 1 soln.
52, 359, 824, {871 or 911}, 960/992
- 1 soln.
52, 359, 824, 928, 943, 992
- 1 soln.
52, 615, 792, 871, 960/992, 975
- Gemani's Double Bill (combines Cutler's 305 and 306)
52, 615, 792, 928, 975, 1024
- 1 soln.
52, 615, 792, 960/992, 975
- Bill Cutler's No. 305. A nice 3x3 slide. gamesandpuzzles.co.uk has it.
52, 615, 856, 928, 960, 975
- 52+928 (DV or PL) makes a 2-piece key
52, 615, 871, 928, 975, 1024
- 1 soln.
52, 615, 871, 960/992, 975
- Bill Cutler's No. 306. - Cutler, Coffin, and Curfs say this may be the most difficult notchable solid burr.
52, 792/911, 824/975, 1024
- The 6-way (Rainbow). 8 apparent assemblies, 6 solutions. An old one sold as "The Zoozzler." Also the vintage "Mikado." B13S.13
52, 792, 824, 960, 975 x2
- 2 solns.
52, 824 x2, 911, 975, 992
- 2 solns.
52, 824, 871 x2, 928, 992
- 1 soln.
52, 871 x2, 928, 960, 975
- 1 soln.

55, 508, 622, 768, 960, 1023
- Derwin Brown's Unique Level 6
56, 94, 156, 704, 1008, 1024
- Stewart Coffin's Triple Slide
56, 276, 792, 832, 975, 1024
- "Chinese Puzzle D" (1 soln.)
63, 480, 512, 766, 896, 1012
- Curfs BC UL7000
72, 112, 448, 511, 990, 1024
- Stewart Coffin's No. 40 Interrupted Slide (1979) - one of the "Fearsome Four"

86, 160, 224, 992, 957, 1016
- JVK #25.2 derivation
86, 256, 911, 992, 928, 1024
- JVK #25.2 - a level 3 design which uses piece #86.

88, 160, 512/768, 992, 1008
- Edward Hordern's modification to Peter Marineau's Piston Burr - 13 solutions, one at level 10
88, 512, 704, 960/992, 1008
- Bruce Love's Dozen. The only burr at the highest level, 12. There are 89 ways to put it together, but most of them don't achieve level 12.
88, 512/768, 922, 1008 x2
- Peter Marineau's Piston Burr - The highest level, 9, with a unique solution.

103, 160, 224, 824, 928, 1024
- Ishino's Millable 5.4
103, 188, 256, 928, 975, 1024
- Jurg von Kanel's jvk25.1 - Note: the notch in piece #256 (X) in my copy of the Wayne Daniel burr set is too short and prevents piece #975 (Q) from being removed, so this one cannot be constructed using the set.
103, 256 x2, 824, 928, 960
- LNRSXX - unique level-5 solution, discussed by Bruno Curfs
103, 256 x2, 928 x2, 960
- LLNSXX - unique level-5 solution, discussed by Bruno Curfs
103, 256, 412, 824, 928, 1024
- Jurg von Kanel's favorite notchable burr
103, 256, 911, 960, 1007, 1024
- B13H.1
103, 508 x2, 824, 928, 1024
- David Winkler's favorite level 5.4 Millable burr
103, 760, 960/992, 996, 1024
- Bill's Baffling Burr; Gemani's Deadlock - 5 moves to release the 1st piece. One of the "Fearsome Four."

109, 188, 736, 928, 1008, 1024
- Bruno Curfs' BC L6000 - nice, 6 moves to free the 1st piece

120, 154 x2, 256, 1024 x2
- Ishino's Notchable 5-Moves 2-Hole - (a set of 42 does not have 2x 154) Note: again, the problem with #256 in the Wayne Daniel set prevents this construction.
120, 154, 188, 928, 1024 x2
- KLMUYY can be made with the set of 42
120, 154, 256 x2, 960/992
- KNOUXX - only multiple level-5 solutions
120, 154, 256, 412, 960, 1024
- Ricardo's burr - brought to my attention via email. Single level 5.4 solution.
120, 160, 256, 512, 880, 960
- Philippe Dubois/Gaby Games - 6 moves to release the 1st piece. One of the "Fearsome Four." Also Arjeu CT757.
120, 188, 670, 928, 992, 1024
- David Winkler's favorite 5.4
120, 188, 792/911, 975, 1024
- Ishino's Notchable 2-Moves 1-Hole #3
120, 188, 871, 928 x2, 1024
- Tumult - try to find the level 7 solution.
120, 792/911, 824/975, 992
- Bill Cutler's Notchable 1-Hole Level 2 - uses only notchable pieces and has only one void - 4 solutions, one at level 2.

126, 615, 820, 856, 928, 1024
- Stewart Coffin's No. 36 Improved Burr (1979) - One of the "Fearsome Four."
144, 495, 702, 975, 990, 1024
- Abad's Level 5.7 Improved Burr
154, 256 x4, 1024
- U.S. Patent 1542148 - Kramariuk 1925.
158, 768, 824, 863, 992, 1012
- Curfs BC UL5000
160, 188, 412, 751, 960, 1024
- Ishino's Millable Unique 5.4.2-Moves 4-Hole
160, 499, 512/768, 926, 1015
- Bill Cutler's Computer's Choice 5-Hole
160, 508, 736, 742, 768, 1015
- Abad's Level 9 Burr
188, 256, 615, 975, 928, 1024
- GLMQXY - this one works like JVK 25.1
188, 256, 768, 824/975, 1024
- Old black Treen Burr seen on antiques site - level 3, 2 solns. (assuming it uses pc #256 rather than 1)
188, 704, 768 x2, 928, 1007
- Ishino's Notchable Unique Impossible Length 10 - 1 solution at length 8, none at length 10
192, 736, 768, 976, 1007, 1008
- Peter Roesler's #G
216, 412, 751, 896, 960, 1024
- Bill Cutler's Eight is Enough

256 x5, 992
- David Winkler's Level 3 - use either of the Fingers 960/992, or 928.
256, 551, 960/992, 992, 928
- Bill Cutler's L5 Notchable - one of 139 designs using only notchable length-6 pieces and having a unique solution
256, 792/911, 943, 960, 1024
- Curfs mentions CDINXY and rates this the third hardest (UL4 #3) of the five level-4 puzzles with unique solutions among the holey burrs constructible using the notchable pieces.
256, 824, 911, 928, 943, 1024
- Curfs mentions CINRXY and rates this the second hardest (UL4 #2) of the five level-4 puzzles with unique solutions among the holey burrs constructible using the notchable pieces. This one works with the Wayne Daniel set and has nice dead-ends.
256, 824, 911, 943, 960, 1024
- Curfs mentions CILRXY and rates this the fourth hardest (UL4 #4) of the five level-4 puzzles with unique solutions among the holey burrs constructible using the notchable pieces.
256, 911, 943, 960, 960/992
- Curfs mentions CINNOX - this gets his "beauty prize" and rates fifth hardest (UL4 #5) of the five level-4 puzzles with unique solutions among the holey burrs constructible using the notchable pieces. Works with the Wayne Daniel set.

311, 768, 867, 924, 1015, 1024
- Bill Cutler's Computer's Choice 3-Hole (Level 7 unique soln) - of 2.5 billion 3-hole assemblies, 198 have level-7 solutions and of those 157 have unique solutions. NOTE: I had previously listed piece 869, but Aaron Siegel pointed out to me that it is equivalent to 867, in this case via a 180 degree rotation about the z axis, then a 90 degree rotation towards you about the x axis.

359/615, 928, 960, 990, 1024
- Abad's Level 4 Ambiguous Burr (maybe try using 992 instead of 990?)
359/615, 943, 960/992, 1024
- Bruno Curfs' FGINOY - you can sub. 856 (J) for 943 (I) - 156 apparent, 4 level 2.2 solns
359, 871, 943, 928, 1007, 1024
- Bruno Curfs' Monster FILTVY - unique level 3 soln, 36 apparent - may be the most difficult notchable holey burr
369, 871, 928, 956, 1000, 1024
- Bill Cutler's Computer's Choice 4-Hole (Level 8 unique soln) - of 4.7 billion 4-hole assemblies, 15 are level-8 and of those 13 have unique solutions. NOTE: I had listed 737 as the lowest piece, but Aaron Siegel pointed out to me that 737 equals 369, via a transform of 180 about the z axis, then 90 degrees away from you about the x axis.

412, 512, 480/704, 704, 960
- David Winkler's complex 5.4 - 1 solution but 143 apparent assemblies, the most for length-6 notchable. (All of these pieces are actually notchable.)
412/670, 687, 1007, 1024x2
- XSOHO Burr - use length-8 pieces for a single level 4.6 solution
416/672, 448, 848, 983,1024
- Level 5.3 "Big Burr"
416, 512, 856, 960, 1013, 1015
- Peter Roesler's #C
448/736, 512, 743, 880, 1015
- Curfs BC UL6000
463, 564, 760, 909, 927, 1016
- Tenyo Brother; also Filipiak #72, if his #10 = 463
480, 511, 512, 989, 1015, 1023
- Peter Roesler's #D
499, 736, 768, 943, 992, 1015
- Rob's Burr No. 1, which has 3 solutions - one at level 3, and two at level 9
509, 511, 792 x2, 788, 1023
- Filipiak #73 MODIFIED by me
512, 476, 757, 956, 1021, 1024
- Bill Cutler's Programmer's Nightmare - requires a rotational move! (Use length-8 pieces.)
512, 734, 871, 928x2, 1007
- Lee Krasnow's Burr - 1 soln. @ 4.6
615, 856, 871, 888, 928, 1024
- Darryl Adams - single level-3 soln.
624, 702, 768, 883, 1015, 1024
- Bill Cutler's Computer's Choice Unique 10 (CCU10). Use length-8 pieces.
702, 768, 883, 944, 1015, 1024
- Brian Young's Mega Six (Mega 6, Mega-6, M6) - a derivative of Cutler's CCU10, also using length-8 pieces but having 20 assemblies instead of 7, yet still a single level 10 solution. Maybe the hardest burr overall? NOTE: In lieu of 883, I had previously listed piece 869, but Aaron Siegel pointed out to me that it is equivalent to 867, in this case via a 180 degree rotation about the z axis, then a 90 degree rotation towards you about the x axis. Aaron also pointed out that 867 should instead be 883, which has the cubie at position 16 removed. See the listing at Jim Storer's site, showing pieces (PDF). This revised piece set is also consistent with the description of M6 having one less cubie than CCU10 - piece 944 has one less cubie than 624.

792/911, 824/975 x2
- Filipiak #71 - 3 solutions.
824, 911, 960/992, 1007, 1024
- B13H.2
856, 871, 911, 960/992, 1024
- Bill Cutler's Bin Cross - presented by Toyo as length-8 pieces which must be assembled inside a slotted glass cage.
871, 911, 943, 960, 1007, 1024
- Curfs mentions CINTVY and rates this the hardest (UL4 #1) of the five level-4 puzzles with unique solutions among the holey burrs constructible using the notchable pieces.

Theory

The recent history of discovery related to the burr puzzle seems to me like the history of world exploration - at first, the "known world" was small and encompassed some well-traveled areas, beyond which lay either the "edge of the world" (for those who thought they had seen all the burrs and only "a few" remained to be found), or a "terra incognita" that stretched off into the hazy distance.

Decades, perhaps even centuries, of exploration served to extend the frontiers of what was known, with some impressive voyages of exploration by intrepid souls using relatively primitive technology. But it was not until the computer age and Bill Cutler that a "satellite view" became available, delimiting the "globe" and showing its full extent - 35 billion assemblies.

Most of that area is "water" - assemblies that cannot be constructed. Roughly 17% is "land" - the 5.95 billion constructible burrs. The "Old World" of the solid burrs stretches across 119,979 assemblies, and features many well-known cities and well-traveled routes. Cutler's satellite view has identified several impressive peaks in the larger world beyond, and much ground remains unexplored.

Are the burr pioneers really "inventors?" Or, like the explorers of old, are they really more "discoverers?"

I don't claim to have "invented" any unique burr puzzles myself, but like others I have spent some time exploring the world that Cutler delimited.

In particular I have been interested in finding high-level (holey) burrs that can be made with the notchable set, at length 6. Bruno Curfs has utilized computer analysis performed by Keiichiro Ishino, and makes several output files available at his site. Bruno mentions and discusses several burrs already.

Here are a few holey burrs made with the notchable set, which I'd like to flag as of interest:

The first is LLMTUY, which I like to call the "Tumult" burr. Its pieces have the numeric IDs: 120, 188, 871, 928 x2, 1024
This burr does not have a unique solution, so it does not, based on what I've seen, get a lot of attention. It has six solutions, the highest at level 7, and does not have any level-1 solution. Of burrs made with the length-6 notchable set, there are only 15 assemblies that can achieve level-7, and Tumult is the one with the fewest assemblies.
In all six of its solutions, three of the pieces retain the same orientation. The orientations of the other three pieces determine the different solutions and level.
Tumult has an interesting sibling, LLMTVY, which substitutes the 1007 (V) piece for the 120 (U) piece. This puzzle actually messes up Jurg's applet, which reports a spurious level-9 solution.
Another nice one is EOOQYY, which has a single level-3 solution but 26 assemblies. The mechanism reminds me of a simple lock - I really like it.
35, 975, 992 x2, 1024 x2
KLMUYY is similar to Ishino's Notchable 5-Moves 2-Hole, but it doesn't need two of piece 154, only one of which is supplied with the typical 42-piece set. It has one level 4.4 solution and one level 5.4 solution.
120, 154, 188, 928, 1024 x2
GLMQXY works like Jurg von Kanel's 25.1. It has two level-5 solutions, which differ by only the orientation of one piece.
188, 256, 615, 975, 928, 1024
KNOUXX has only multiple level-5 solutions.
120, 154, 256 x2, 960/992

The core:

  +----+               
 /  1 /|               
+----+ |       +----+  
|    | +----+-/  2 /|  
|    |/ 4   5+----+ |  
+    +       |    | +  
| 3 /        |    | |  
|  +----+----+    + |  
+--|  6   7    8  | +  
   |              |/   
   +    +-|/-+----+    
   |    | +  10        
   |  9 |/             
   +----+

Of the 314 solid puzzles that can be made with the 25 notachable pieces, there are 158 that use the key piece #1. If you start with 6 Y pieces and make one key piece, you use up 10 of the 20 "floating" interior cubies. The "core" shown here is then composed of the 10 interior cubies that remain to be distributed among the other 5 pieces.

Imagine that the key piece goes into the page resting on the plane formed by the core cubies labeled 4,5,6, and 7. The other 5 pieces would start as instances of the "minimal" piece #1024 (Y), and acquire some share of the 10 cubies of the core.

Note that no single piece can have all 10 - this would result in a second key piece, which some reflection should convince you doesn't work.

I have chosen an arbitray orientation for the other 5 pieces, which I'll call P1 through P5, resulting in the particular core shape shown. Other shapes are possible. Imagine P1 through P5, oriented around the core as follows.

P1 is vertical on the left; the 2-cubie notch of P1 fits on 1 and 3, and its "arms" face right.
P2 is vertical on the right; the 2-cubie notch of P2 fits on 2 and 8, and its "arms" face left.
P5 is horizontal, into the page below the key piece, and fits on 9 and 10, with its arms facing up.
P3 is horizontal across the page in front, with the notch upwards and the arms facing the rear.
P4 is horizontal across the page in the rear, with its notch upwards and its arms facing the front.

The following chart shows how the floating pieces might be distributed, converting P1 through P5 into pieces other than Y. Note that cubies 1 and 3 must be allocated as a pair. (Why? Because if they are split up, it results in some pieces which are not notachable.) Likewise for the pairs 2 and 8, and 9 and 10.

	1 and 3	2 and 8	4	5	6	7	9 and 10
P1		x		x		x
P2	x		x		x		x
P3	x		x	x			x
P4		x			x	x	x
P5 (opp. key)	x	x

Now, consider the possibilities for building up P5...

P5 plus	(none)	5	7	(5,7)	(9,10)	(4,5,9,10) (6,7,9,10)	(4,5,6,7,9,10)
equals	Y	W	X	V	J	I	H

Note that, given the chosen orientation, P5 cannot include 4 or 6 without including 9 and 10 - they would be hanging off in space unsupported.

So, what's wrong with this analysis? It gives an incomplete list of possible pieces for P5! Missing are: E, G, Q, U, P, and S. Why? It is a consequence of my original arbitrary orientation of the Y pieces. P5 has access to two additional cubies on each end, provided two things happen:

either P1 or P2 must be reversed so its notch is on the other side
either P3 or P4 (but not both) must be piece M

P5 plus	(none)	5	7	(5,7)	(9,10)	(4,5,9,10) (6,7,9,10)	(4,5,6,7,9,10)
equals	Y	W	X	V	J	I	H
plus 2 equals	Q or U	S	P	not possible	G	E	not possible

The two extras have to be taken on the same side the M piece will be placed - they cannot come one from each side since that results in internal corners again. This is only possible due to the symmetric nature of piece M, which allows its crossbar to be fitted inboard of where crossbars normally go. If you try this with my LiveCube pieces described above, some of the yellow "internal" cubies of the M piece will show on the outside due to the necessary rotation.

For puzzles using the key piece A, piece M can never appear more than once.

Here is a list of the 17 configurations employing one of E,G,Q,U,P, or S opposite A. All require an M. There are only 5 other configurations that use M - these do not require its rotation. All are very easy.

AH-YM-YY

AI-VM-YY

These are three solutions for the same pieces:

AI-WM-YX

AI-XM-WY

AI-YM-WX

AE-YM-YY
(There is only one AE since E uses 6 of 10 available floating cubies, and M the other 4, demanding that all the rest be Y pieces.)

AG-VM-YY

AG-WM-YX

AG-XM-WY

AG-YM-WX

AQ-VM-QY

AQ-WM-QX

AQ-XM-OY

AQ-YM-OX

AU-VM-YU

AU-WM-YT

AU-XM-WU

AU-YM-WT

AP-WM-QY

AP-YM-OY

AS-XM-YU

AS-YM-YT

Let's look at how the remainder of the 158 configurations break out based on the choice for P5. One would assume, the more floating cubies used by P5, the fewer associated configurations.

The fewest should occur when P5 = H, using 6 of the 10. One might think the remaining 4 could be split as follows: 4/0/0/0, 3/1/0/0, 2/2/0/0, 2/1/1/0, 1/1/1/1. However, P5 as H has used 4,5,6,7,9, and 10, leaving the pairs 1/3 and 2/8 which cannot be split. This means only 4/0/0/0 and 2/2/0/0 are possible divisions. We've already seen AH-YM-YY; the M uses the remaining 4, requiring 3 Y pieces.

There are only 4 AH configurations, as follows.

AH-YM-YY (4/0/0/0) - both pairs part of same horizontal piece M
(Note: making each pair part of a different horizontal piece P3=U and P4=U makes the burr impossible to construct!)
AH-YQ-JY (2/2/0/0) - one pair to a horizontal piece and one pair to a vertical piece
AH-YU-YJ (2/2/0/0) - mirror image of above
AH-YY-JJ (2/2/0/0) - both to vertical

The next smallest class should be the AI configurations. The I piece used 4 out of 10, leaving 6. 1/3 and 2/8 still must be assigned as pairs, but 4 and 5 can be independently allocated to different pieces. The possibilities: 6/0/0/0, 4/2/0/0, 4/1/1/0, 3/2/1/0, 2/2/2/0, 2/2/1/1.
There are 16 AI configurations as follows:

AI-QN-YY (4/2/0/0) both horizontals, 1/3 and 2/8 separated

AI-QO-XY (3/2/1/0)

AI-UR-YY mirror of QN

AI-UT-YW (3/2/1/0)

AI-VM-YY (4/2/0/0) both horizontals, 1/3 and 2/8 together in M

AI-VQ-JY (2/2/2/0)

AI-VU-YJ mirror of VQ

AI-WM-YX (4/1/1/0)

AI-WQ-JX (2/2/1/1)

AI-XM-WY (4/1/1/0) mirror of WM

AI-XU-WJ (2/2/1/1)

AI-YF-YY (6/0/0/0) an anomaly with inside cubies showing

AI-YM-WX (4/1/1/0) same pieces as WM-YX above

AI-YN-JY (4/2/0/0)

AI-YR-YJ (4/2/0/0) mirror of YN

AI-YV-JJ (2/2/2/0)

V uses only 2, leaving 8 - the pairs 1/3, 2/8, and 9/10, and 4 and 6.
The 16 AV configurations:

AV-QO-YT (3/3/2/0)

AV-UT-OY mirror of QO

AV-WK-QY (5/2/1/0)

AV-WP-GY (4/3/1/0)

AV-WT-QJ (3/2/2/1)

AV-XL-YU (5/2/1/0) - a little tricky

AV-XO-JU (3/2/2/1)

AV-XS-YG (4/3/1/0)

AV-XW-JG (4/2/1/1)

AV-YK-OY (5/3/0/0)

AV-YL-YT (5/3/0/0)

AV-YO-JT (3/3/2/0)

AV-YQ-DY (6/2/0/0)

AV-YT-OJ (3/3/2/0) - very common design (red, licorice stix, pendant)

AV-YU-YD (6/2/0/0)

AV-YY-JD (6/2/0/0)

Not yet shown: AJ (21), AW (24), AX (24), AY (36).

And that leaves the 156 configurations that don't use the key piece #1.

Traditional 18-piece Burrs

This section is about the "Traditional" 18-piece Burr.

This type of burr can be visualized as having a 6-piece burr shape at its core, but instead of 2x2x2 pieces crossing, it has 6x6x6. Each group of 6 pieces along an axis is arranged in a 2x3 block. The minimum length of a piece is 8 units - pieces are typically 2x2x8.

Willem van der Poel seems to have designed the first 18-piece 6x6x6 burr, in 1951-1953 - this type of burr is a much more recent development than the Traditional 6-piece Burr. In this case, "traditional" refers to the canonical 6x6x6 shape rather than hinting at any deep history. (Other shapes or arrangements of 18 pieces are possible.) Van der Poel's burr is known as the Grandfather 6x6x6 18-piece burr. The Grandfather burr is discussed on Pete Roesler's site, where you can read a brief history written by van der Poel. Willem made a copy by hand from Beech wood - that copy is now in Jerry Slocum's collection. Willem's design is level 3.2.4. 1.1.2.

Ishino has a catalogue of length-8 pieces here. Ishino also has a selection of 18-piece burr designs, and a table of some designs, listed with piece codes. The burr diagrams used below are Ishino's.

As discussed in the section on Traditional 6-piece Burrs, Bill Cutler completely analyzed those. However, as of this writing in Feb. 2011, no-one has yet performed an analysis for the Traditional 18-piece Burr.

In van Delft and Botermans' Creative Puzzles of the World, van der Poel's puzzle is shown on page 71. In Slocum and Botermans' Puzzles Old and New, plans for an 18-piece burr are shown on page 71 - Ishino calls this one Unnamed 18 Piece Burr #1. Its pieces are length 10. (Maybe designed by Gillett as noted in this thread on the PuzzleWorld forums?)

Frans de Vreugd is a notable collector with an interest in high-level burrs - Frans has published nice articles on the topic in CFF #80 (Nov. 2009) Recent 18-Piece Burrs, and CFF #82 (July 2010) More 18-Piece Burrs, as well as an article in the book A Lifetime of Puzzles: A Collection of Puzzles in Honor of Martin Gardner's 90th Birthday - Extreme Puzzles on p.195.

At the higher levels, even disassembly is a challenge. Re-assembly without instructions becomes almost impossible.

Guillaume Largounez posted an interesting account of his attempts to construct and solve the most difficult 18 piece burrs, at the PuzzleWorld Forums. His conclusions are in this post.

Some quotes from Guillaume:

"Most of these puzzles propose a disassembling challenge only. The puzzle is given assembled, and the goal is to find the way to take the pieces apart. In all these puzzles, the sequence of moves is not trivial. This is not 'one move allows the next one, that allows the next one etc.' There are choices to be made. A random exploration of possibilities may be enough to find the solution of the disassembling challenge, but not always."
"I think that in order to maximize enjoyment, and [offer] an assembling challenge in addition to the disassembling one, 18-pieces burrs designs should have only one possible solution, but also one possible assembly and no more."
"Among [the commercially available puzzles], Condor's Peeper ... gives the real enjoyable feeling of high level 18-pieces burrs. It is something similar both to labyrinths, and chess game. Like in labyrinths, you explore paths, with crossings, where you have to choose between two or more ways to go on, without knowing which is the right one. Some ways seem to bring you closer to the exit, but things are not always what they seem. You find many dead ends, and must go back in order to try another ways. Sometimes, after a long way, you realize that you are back in the position that you already were before. And sometimes, when you feel lost, this is like a chess game."

Goetz Schwandtner is another collector with an interest in high-level burrs - you can see his collection online at his website Extremely Puzzling. Goetz says, "Level 138 and above puzzles are very difficult even with a BurrTools solution at hand. These high-level puzzles have so many internal voids and intermediate states that tend to make moves by themselves that you can easily get lost in the solution."

Rob Chiniquy has designed a level 17 18-piece burr - you can read about it at his blog, "oddly, hippo."

In the quest for higher levels, in order to exclude lower-level configurations of a given set of pieces that have more than one solution, the pieces can be colored or marked in some other way to indicate a preferred/required solution configuration. This can also help make reassembly tractable. It should be acknowledged that some folks don't enjoy higher-level puzzles, since solving starts to seem like too much work. Also, some folks believe it is inelegant to resort to coloring or marking pieces to exclude low-level solution assemblies.

The simplest piece is arguably x00FFFF

The earliest designs (e.g. Grandfather, Lovely) are composed of a core 6-piece burr, surrounded by a "cage" of relatively simple pieces, usually x00FFFF. The animation shown here illustrates the core 6-piece burr and how it is surrounded by a cage of 12 additional pieces. Of course, what makes each design unique will be the piece notchings and how they fit together.

According to Ishino, in 2003 Paul Blake designed a level 4.4.3.4.2. 5.3.4.2.2. 1.2.1.2 using 18 of x00FFFF, called Simply Complex. I entered the traditional 18-piece burr shape into BurrTools, along with 18 copies of the x00FFFF piece - the run finished very quickly in only 1.4 minutes. My run gave 1960 assemblies, of which 1372 are solutions. The highest level found was 4.3.1.4.2. 2.2.2 with 29 moves; the highest number of moves is 32 for a level 1.3.1.3.3. 4.3.3.3 solution. My 1960/1372 statistics agree with Ishino's, but my run did not find the purported level 4.4 (39 move) solution, so there seems to be some error somewhere - or we are counting moves differently when several pieces move together, or when pieces move further than one unit in a given direction.

Designers have sought to create higher-level puzzles:

Year	Designer	Level	Name	Source
1980s	Bruce Love (by hand)	18.2.5.4.2.1.2	Lovely Burr	Bill Cutler's website
1999	Brian Young (by hand)	19.4.1.1.7	Coming of Age Mark II	Mr. Puzzle
2002	Goh Pit Khiam	33.7.2.1.2.3.3.1.3.1.2	Burrloon
2003	Jack Krijnen	43.2.2.2.3.1.2	Tipperary
2005	Goh Pit Khiam and Jack Krijnen	50.2.1.1.1.1.1.2.3	Burrserk
2008	Alfons Eyckmans	59.2.6.1.2.3.2.2.2.1.1.1.1.1.1.2	Condor
2008	Krijnen	62.4.21.1.2.2.1.1.1.2.2.2.1.1.1.2	Condor's Peeper	Mr. Puzzle
2008	Jan Naert	65.1.2.1.1.4.3.2.2.2.2.1.1.2.2.2	The Monster
2009	Eyckmans	113.14.7.4.9.14.3	Phoenix Cabracan
2010	Krijnen	138.7.5.1.1.2.1.1.2.2.2.1.1.1.1.2	Burrly Sane for Woodworkers
2010	Krijnen	148.3.4.3.10.13.3	Burrly Sane for Professionals
2010	Eyckmans	150.6.3.10.3.1.1.1.2.4.2.1.2	Tiros
2010	Krijnen	152.7.9.5.11.14.4.1.1.1.1.2	Burrly Sane for Extreme Puzzlers
2011	Krijnen	100.10.3.2	Century
2013	Krijnen & Eyckmans	156.6.8.1.1.3.4.2.3.2.1.1.1.1.1.2	Excelsior
2013	Krijnen & Eyckmans	166.6.8.1.1.1.2.4.1.1.2	Supernova	Arteludes

It seems like Jack Krijnen and Alfons Eyckmans are in a duel to devise the highest-level 18-piece burr! Level 166 is the highest at the time of this writing, October 2013. The higher-level puzzles following Phoenix Cabracan are based off of it. Guillaume says, "Among the highest level burrs, Tiros (level 150), and Burrly Sane for Extreme Puzzlers (level 152) ... are very similar. The 87 first moves are exactly identical (they are both variants of the Phoenix Cabracan)."

In May 2020, after a long wait, the beautiful set below arrived at my mailbox - the
Phoenix Family Burr Set - designed by Jack Krijnen and Alfons Eyckmans and hand made by Jack Krijnen
from zebrano, birch and amouk for the pieces, with mahogany, hornbeam, and cedar for the box.
45 pieces can be assembled into at least 12 different but related high-level "traditional" 18-piece burrs,
including Supernova, Excelsior, Barones, Burrly Sane for Extreme Puzzlers, and Tiros.

Phoenix Family Burr Set - Krijnen

Here is a table of the individual 18-piece burr puzzles I have obtained (or wish to show the pieces of):

SuperNova - designed by Alfons Eyckmans and Jack Krijnen,
and made by Alfons Eyckmans
from Maobi, Bird's Eye Maple, and Afzelia.
Very nice fit, with smooth slack-free movement.
At level 166, this is the world's current highest-level 18-piece burr,
made for me by one of its designers!

Grandfather 18-piece Burr - van der Poel - Pelikan

I acquired an instance of Willem van der Poel's The Grandfather of 6x6x6, made by Pelikan, in an auction from Stewart Coffin's collection. Willem's exchange puzzle at IPP24. Includes a sheet with the 50-year history of the puzzle and instructions.
See it at Ishino's site.

Van der Poel's Grandfather 6x6x6 18-pc burr (rough handmade copy - unknown craftsman)
I also have a rough handmade copy but I don't know who made it. This copy has one piece that differs from van der Poel's design - instead of piece "G" there is another "H."

According to Willem, the Arjeu CT52 was an unauthorized copy of his design. The Dalloz Urdin is the same.

You can see solutions at Les Casse-Tete de Chantal.

Van der Poel's Grandfather 6x6x6 18-pc burr (large copy - unknown craftsman)

I received this large example of the van der Poel burr as part of a group of wooden puzzles. I don't know who the craftsman is. A couple of pieces are slightly different from the official design, but the assembly sequence is the same.

Here is a wooden "traditional" 18-piece burr from France. It is a fairly simple construction, and it is not a copy of van der Poel's Grandfather Burr. It is from a company called Grandjouan (Great Toys) and according to various sources, including the solution sheet that came with my example, the burr is called Damier. Unfortunately no source I found has identified the designer or its date of production. In addition, the name "Damier" has been applied to several different puzzles.

Damier 18-piece burr - Grandjouan France

A design by Bruce Love called the Lovely Burr.
Level 18.
Only 1 solution.
Made by Jerry McFarland, from Walnut and Mahogany.
You might find one at Bill Cutler's website.
Brian Pletcher blogged about this puzzle.

Coming of Age Mk.II - Mr. Puzzle Australia
An 18-piece 6x6x6 burr designed by Brian Young, without the use of a computer. There are multiple solutions - the highest level is 19. It was analysed using BurrTools by Andreas Roever and he found a level 14.10.3.2. 5.11.10. That makes 65 moves for complete disassembly. Here is a YouTube video of Brian assembling this burr.
Here is a YouTube video of a level 19.5.1.1. 7.1.1.1.2 assembly. Here is another YouTube video, of a level 16.3.1.1. 3.4.1.1.2 assembly.

Brian gives the following statistics based on Andreas' analysis:

Highest first level is 19. There are 2 such solutions, very similar. Both take 46 moves to disassemble.
Other high level solutions exist at level 16, level 14.10, ...
Brian prefers 2 solutions with level 14.10.3.2. 5.11.10, taking 65 moves to disassemble - more than required for Burrloon, which requires 64 moves at level 33.8...
Analysis took 1214463 seconds = 14.06 days
880338023 assemblies found, 7621 solutions

Condor's Peeper - Krijnen - Mr. Puzzle
Condor's Peeper
designed by Jack Krijnen
made by and purchased from Mr. Puzzle Australia
Level 62
Only 1 solution, respecting the color scheme.

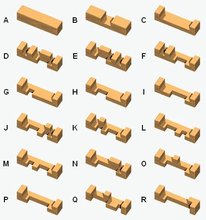
The Dragon Burr - a burr having 18 unique pieces. From Creative Crafthouse. Rated as one of their most difficult puzzles.
Level 1.1.3.2.2
This was originally designed by Maurice Vigouroux in 2003 and called simply "The 18 Piece."

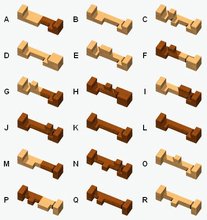
Tiros, shown here, is an 18-piece burr designed and made by Alfons Eyckmans. I obtained this in a trade with French puzzler Guillaume Largounez.
Tiros requires 150 moves to get the first piece out!
Guillaume suggests, "If you want to turn mad someone who owns a copy of the Tiros burr, disassemble it until pieces J and K are out, swap them, and rebuild the whole puzzle without the piece G (it can't fit if J and K are swapped). If the way Burrtools gets pieces J and K out is the shortest, solving the puzzle back to its assembled configuration should take 331 moves."

18 piece burr #3 - Not known who designed this
Level 1.2.1.2.1.1.1.1.2
Available from Creative Crafthouse
Here is a YouTube video of Dave showing three 18 piece burrs offered by Creative Crafthouse.

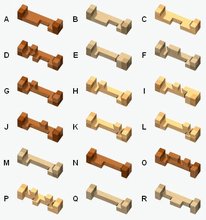
Burrly Sane for Woodworkers - Jack Krijnen

Burrly Sane for Woodworkers - designed and made by Jack Krijnen
Level 138.7.5.1.1. 2.1.1.2.2. 2.1.1.1.1.2
Thanks, Jack!

Burrly Sane for Extreme Puzzlers - Jack Krijnen

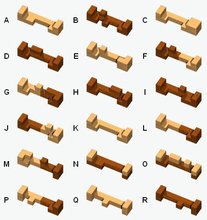
Burrly Sane for Extreme Puzzlers - designed and made by Jack Krijnen
For a while was the record holder for highest level traditional 18-piece burr, at 152.7.9.5. 11.14.4.1. 1.1.1.2.

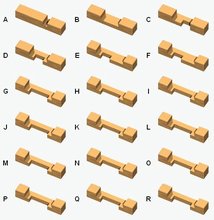
In Slocum and Botermans' Puzzles Old and New, plans for an 18-piece burr are shown on page 71 - Ishino calls this one Unnamed 18 Piece Burr #1. Its pieces are length 10. (Maybe designed by Gillett as noted in this thread on the PuzzleWorld forums?) Creative Crafthouse sells this one as their 18 Pc. Burr #2.

Arjeu CT666 (aka Super Croix (Cross) or Ushuaia)
Gift from Jeff Taylor
Designed by Jean-Paul Pierlot. No internal holes. Offered by Arjeu circa 1988. Pieces shown in photo.
Here is a link to the solution in a French puzzle forum.
Here is a link to a solution video on YouTube, and another in lower resolution.

Van der Poel wrote that Pierlot designed 3 versions with no internal holes.
I read on the PuzzleWorld Forums that another is called "Tricolore."
Peter Knoppers' defunct site had the piece diagram shown above.

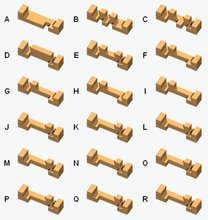
Burrloon pieces
(I don't have this puzzle.)

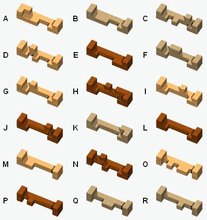
Phoenix Cabracan pieces
(I don't have this puzzle.)

Century burr - an 18-piece burr at level 100, designed by Jack Krijnen, produced with Jack's permission by Colin Gaughran.

Bill Cutler designed the Slider and used it as his exchange for IPP30.
It looks innocent enough, but judging by the internals, it is not your typical 18-piece burr!
It is made from Walnut, by Jerry McFarland.
I obtained a copy at Eureka Puzzles.

Vertigo from Pentangle is also not quite "traditional" internally.

The Diagonal Burr, Diagonal Star, and Cylindrical Pieces

These are examples of the classic 6-piece Diagonal Burr.

The diagonal burr puzzle can be made from 6 identical pieces, each having two notches, but sometimes appears with a key piece that really isn't necessary. It can be [dis]assembled either by exploding/collapsing all the pieces simultaneously, or the pieces can be composed into two 3-piece halves that will easily slide together.

The earliest relevant U.S. patent is 393816 - Chandler 1888. Also see 779121 - Ford 1905.

From left to right: Knobulus by Haba, the vintage Jane's Puzzle by Drueke, and a vintage acrylic diagonal burr, the Prism Puzzle, issued in 1970 by the Pacific Game Company of N. Hollywood CA. The plastic "Lady" burr shown later on is another example.

This clever version of the diagonal burr is called Insoma. It has a hollow center in which a Soma Cube must be constructed simultaneously with the burr, since all but one of the Soma pieces are connected to the burr pieces! Designed and made by Mr. Puzzle Australia (Brian Young), and purchased at the NYPP 2008.

These are examples of the Diagonal Star. It can be derived from the diagonal burr by beveling the ends of each of the pieces. After the traditional six-piece burr, I would say this is one of the best-known and most widely manufactured designs. The earliest patent seems to be Swiss - CH245402 - Iffland 1946; Iffland's design includes the unnecessary key piece. Clever variations exist where the inside is hollow, forming a cubic cavity. Read more about this puzzle in Chapter 7 of Stewart Coffin's The Puzzling World of Polyhedral Dissections. The shape is formally known as the first stellation of the rhombic dodecahedron. (See Steven Dutch's site for a nice explanation of stellations of polyhedra.) The rhombic dodecahedron also has a second and third stellation.

The nice wooden version on the left was a gift from Arteludes (thanks!); the next three plastic versions are all fairly small and were accumulated here and there; the pale wooden version is common and inexpensive; the plastic Stumpa 2 has an un-notched key piece, with two other pieces each of which therefore has an extra notch. It was issued by Executive Games Inc. of Dorchester Mass.

Below is a Micro Diagonal Star in its own small box - made by John Polhemus, sold via his wife's Etsy store Silly Sheila Designs.

Starburst - a twelve-piece version of the Diagonal Star puzzle, 3D printed by Lee Krasnow.
Check out Lee's Etsy shop Pacific Puzzleworks.

Gift Burr - designer unknown, made by Eric Fuller
from White Oak. Six unconventional pieces form a conventional diagonal star.

Star Cluster Puzzle Set - designer unknown, made and exchanged at IPP38 by Allen Rolfs.
This copy purchased from Allen has a Walnut box and updated puzzle list.
The set contains all possible (seven) different piece types that can be used to construct a traditional diagonal star puzzle, labeled A through G.
Based on analysis by Bill Cutler, there are 52 possible puzzles.
Sadly, there is no construction that uses six different piece types.
Interestingly, the "Gift Burr" from CubicDissection is number 41 - it uses pieces { C, D, D, E, F, G }.

The Diagonal Burr can also be made from rounded or cylindrical pieces, and the tips of the pieces can be rounded off or otherwise shaped as well.

This is called the "Asteroid" from Bits and Pieces. It has the same internal structure as the diagonal burr, but the pieces have been rounded off on the outside. It's not very precisely made, so it doesn't hold together very well.	This is The Ball by Charles O. Perry. I got it at the MoMA shop when I used to work in Manhattan. The brass pieces are cylindrical, with curved ends. The notches are cylindrical, too. It relies on a small spring-loaded ball-bearing and a corresponding detent to hold the key piece in place. I found an acrylic version, too (the MoMA shop used to sell it).
Large Acrylic Ball Burr provenance unknown, but not Perry Shown in comparison with Perry Brass and Acrylic Ball Puzzles
This 6-piece burr has the same internal structure as the Perry Ball (without the detent and spring/ball), but this is made of Kel-Tec bullets! Fortunately they're not live rounds. This was an advertising premium at a gun show.	Skor Mor's Log Jam - this is a rounded version of the diagonal burr. There was a brown plastic version, too, called Stumpa 1.
Burr from Lee Valley Tools a substantial metal 6-piece burr
The Kong Puzzle "Four pounds of metal mayhem" - an interlocking burr with cylindrical brass pieces, from The Kong Puzzle Kickstarter campaign, by Two Brass Monkeys. Packed in its own aluminum briefcase.
The Pygmy and Marmoset Burrs from Two Brass Monkeys Much smaller than the earlier Kong puzzle, but having the same target shape and numbers of pieces, though each with different notchings.

This is the Sequential Star by Lee Krasnow. I bought one from him at IPP26, where it won an Honorable Mention in the Design Competition. It is the "little brother" to his Barcode Burr. Lee has incorporated a sequential opening mechanism into the traditional diagonal star, making this a much more interesting puzzle.

Each of the six burr pieces is composed of three units - a center unit and two end units - held together by 18-8 stainless steel alignment pins and strong neodymium magnets. If undue pressure is applied to the puzzle in the wrong way, a piece can "burst" into its components - but it is easily re-assembled with no harm done. The end units are made of Macassar Ebony and are precision cut to beautifully sharp edges and points. Lee hooked up a CNC feed to his sled and the cuts were made on his table saw under computer control. The center units are made of a kitchen countertop material called Richlite - a sort of plastic-infused paper, which is climate-stable and machines nicely. Each end unit contains a peg that rides in grooves cut in the center units of adjacent pieces. The groove patterns are carefully contrived so as to dictate a particular sequence of moves through which you must navigate the six burr pieces in coordination, until the assembly finally can be slid apart into two 3-burr halves. The grooves were cut using Lee's CNC milling machine.

This is an enlarged construction related to the Diagonal Star,
called variously the Chestnut Burr, the Asterisk, the Snowflake, and the Gem Cut Puzzle.
It has 24 pieces.
The Chestnut Burr appears in Wyatt's 1946 Wonders in Wood on page 36.
My copy is fairly small, and I do not know who the craftsman is.

Kumiki Puzzles

Kumiki puzzles appear in neither Catel's catalog of 1785 nor in Bestelmeier's catalog of 1793-1823 - both of which include only the interlocking Small Devil's Hoof (a traditional six-piece burr) and the Large Devil's Hoof (a cage-style burr). Figural/representational Kumiki puzzles were invented in Japan in the 1890s by Tsunetaro Yamanaka (1874-1954). According to the Indiana State Library, "He designed and constructed intricate puzzles that resembled buildings and vehicles, not just abstract shapes like spheres and cubes. Today, his descendants continue to carry on the tradition, including his great grandson, Tadaaki Yamanaka." Kumiki puzzles were popular after World War II and many were imported by the company Shackman.

The Japanese word "Kumiki" roughly means "to join/weave/interlock wood together." Japanese craftsmen have a tradition of constructing earthquake-resistant wooden shrines using interlocking pieces without metal fasteners/nails, and Kumiki puzzles may have served as practice projects. Cleverwood (now defunct) had a nice write-up about Kumiki puzzles.

Here is a link to John Childs' extensive Kumiki collection.
Frank Potts has a wonderful Kumiki collection.

Kumiki puzzles are usually inexpensive, and made from unfinished Japanese Magnolia ("Ho") wood - but modern versions have appeared in plastic. I group into this category any puzzle with a characteristic 2-piece T-shaped key, but there are four distinct sub-categories:

Oshi - push the key piece out
Mawashi - twisting key piece
Kendon - remove a piece by moving up and down or left and right
Sayubiki - simultaneously remove two key pieces

The Kumiki Cube, Sphere, and Barrel

Perhaps the most commonplace Kumiki puzzle is the classic 12-piece Cube. The related Sphere and Barrel puzzles share the same basic internal architecture though they have different external shapes. Other truncations of the cube have appeared.

Classic Kumiki Cubes	Pieces of the Kumiki Cube	Kumiki Cube assembly instructions from Wyatt's 1928 Puzzles in Wood
Kumiki Spheres and pieces
Kumiki Barrels and pieces
Truncated Cubes - The Cornered Cube from Wallingford Toy Works is a very large version of the usual kumiki cube, with a beveled corner. Also shown are Hidden Passage from SiamMandalay, and a generic Kumiki truncated cube.		An Octagonal Prism
The Daruma Man is painted on an oval form of the barrel.

The Kumiki Ball Burr / Fireman's Standard

The Kumiki Ball Burr is an elaboration of the traditional six-piece burr, where one of each pair of opposing bars has an extra notch near each tip, to accomodate curved outlier pieces. These curved pieces give the Ball burr its interesting shape, but do not in general add to the complexity of the assembly other than posing a dexterity challenge. Since a six-piece burr resides inside, not only can the Ball burrs differ in appearance due to varied outlier shapes but they can also employ different burrs at their cores.

The Ball Burr appears in Joseph Bland's 1890 Mr. Bland's Illustrated Catalogue of Extraordinary and Superior Conjuring Tricks, etc. where it is called the Mystery. It also appears in the 1929 Johnson Smith Catalog where it is unglamorously called No. 3095.

I also found an image of an original instruction sheet on which it is called the Fireman's Standard.

The Chinese Ball Puzzle from Bell of the U.K.
A vintage plastic example of the Kumiki interlocking Ball burr.

Chinese Ball Puzzle - Bell

The Kumiki Cage Burr

The Kumiki Cage Burr employs twelve interlocking bars to form a cubic cage - often a simple wooden sphere is trapped inside. The solution entails finding bars that rotate in place to align with the notches in adjacent bars, thus freeing those bars to be removed.

Besides the traditional Kumiki wooden versions, this design has appeared in plastic versions as well: Trickstix by Harris - see U.S. Patent 2473369 - Harris 1947 - and the Adams' Locked Blocks puzzle.

Here is an example of an extended cage burr - in this case extended linearly into three sections. A ball can be enclosed in each section. Assembling this from scratch can be fairly challenging - even using the accompanying instructions is of limited help since they are drawn so unclearly.

Other Kumiki Burrs

Kumiki Burrs

Yamanaka Kumiki Burr from the Yamanaka Kumiki Works
54 pieces in four different types assemble to make
an attractive symmetrical structure.

Yamanaka Kumiki Burr - Japan
I bought this burr in Japan. It is made by the Yamanaka Kumiki Works. It is the "Masu Model."

Vintage Kumiki Step Burr
Step Burr - vintage Kumiki

Vintage Kumiki Spike Burr
Spike Burr - vintage Kumiki

Kumiki Figural Puzzles

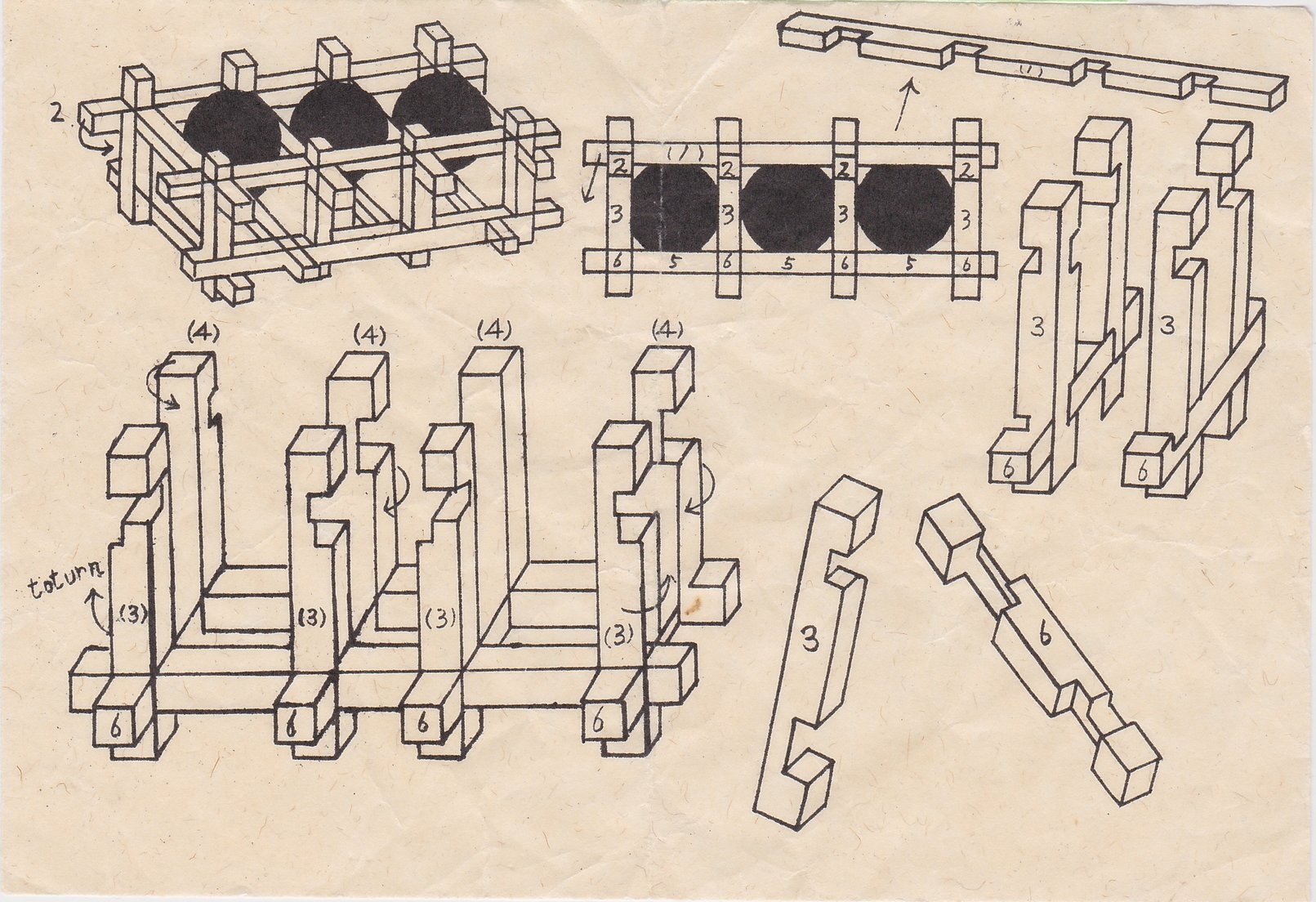
Shackman Clown - part of a fairly rare set of figures. Discussed in Slocum and Botermans' "The Book of Ingenious and Diabolical Puzzles" on page 86.
Shackman Man in Vest
Shackman Man in a Vest - part of a fairly rare set of figures. Discussed in Slocum and Botermans' "The Book of Ingenious and Diabolical Puzzles" on page 86.

Vintage Comic Man Puzzle
I was pleased to find a Shackman Comic Man puzzle in its original box. I have a similar puzzle, also in its box, but with a different label and appearance. A comparison photo is included.

Sombrero Man - I am unaware of the provenance of this puzzle.
It is similar to the puzzles in the Shackman Clown series, but Jerry Slocum has kindly checked his extensive collection of vintage Shackman catalogs and cannot find any reference to these.
Frank Potts believes they were made in Germany - he has a similar puzzle - an accordion-playing sailor.
Jerry Slocum believes these were made in Mexico.

Soccer Man - I am unaware of the provenance of this puzzle.
It is similar to the puzzles in the Shackman Clown series

Kumiki Cigar-Smoking Man - may have been made in Germany
You can see further examples of different figures at Frank Potts' website.
Bulbo Bulbo
Bulbo Bulbo Bulbo Bulbo
A vintage plastic puzzle figure, made in England, called Bulbo, with its original box.
Similar to the Shackman wooden figures.
Fellow Kumiki collector Frank Potts tells me the box is wrong for this puzzle - but this is how I received it from England.

Small Kumiki Pagoda Kumiki Pagoda instructions
Kumiki Pagodas
Two large and one small.
With instruction sheet on very flimsy paper.

Kumiki City Hall, with instruction sheet.

Kumiki Palace

Kumiki Shrine - Yamanaka Kumiki Works Japan

Kumiki Golden Gate Bridge - Smith Novelty Co.

Kumiki Empire State Building
A simple one but I really like it!

A Kumiki Pyramid.

Kumiki Space Needle
Kumiki Space Needle - a souvenir of the 1962 World's Fair in Seattle.
An iconic piece I had been after for a while.
Unfortunately while it looks great, its interlocking architecture is underwhelming
in comparison to the usual better-engineered Kumikis.
But I do love the box art.

A nice, large Kumiki Tori Gate

Kumiki Totem Pole

Kumiki Cabin Kumiki Cabin Bank
Kumiki Cabin - another version with windows and a coin slot in the top. Kumiki Saturn Group
Kumiki Stemmed Group - a group of three Kumiki puzzles,
each with a "stem" - Saturn, Barrel, and Strawberry.

Kumiki Ball and Bat
Kumiki Bowling Pin
Kumiki Bottle

Kumiki Geta - a pair of Japanese wooden sandals

Kumiki Dragonflies
Kumiki Pistols
Yamanaka Kumiki Elephant instructions
Kumiki Elephants - The larger piece is a beautiful and substantial
wooden interlocking elephant puzzle from the Yamanaka Kumiki Works.
Kumiki Elephant - Ball Body
This Kumiki Elephant is based on the Kumiki Sphere.
Giraffe puzzle - Yamanaka Kumiki Works

Yamanaka Kumiki Works Giraffe
Kumiki Hippo Puzzle - Yamanaka Kumiki Works
Yamanaka Kumiki Works Hippopotamus

Kumiki Lion instructions
Kumiki Lions
with instruction sheet on very flimsy paper
Vintage Kumiki Lion

Kumiki Pigs
Large Kumiki Pig
A larger Kumiki Pig
Vintage Kumiki Piglet
Piglet - vintage Kumiki
I found a Kumiki Pig much larger than those I had:

In this group photo it's the huge one in the back.
The piglet is in the foreground, followed by the large pig and the "regular" pig.

Kumiki Dog
Kumiki Mouse
Kumiki Horse

Vintage Kumiki Bambi
"Bambi" - vintage Kumiki

Kumiki Cat

Kumiki Bird

Kumiki Alligator

I found a large Kumiki Alligator, shown with the small one I had:

Kumiki Cow
A butcher's version marked with cuts of beef.
Kumiki Fox
by Mi-Toys
Kumiki Camel
by Mi-Toys

I found a Kumiki Cow design I didn't have:

Kumiki Swan
by Mi-Toys
Kumiki Ladybug

Kumiki Turtle

Kumiki Kangaroo - and that's baby Joey in her pouch!

Kumiki Penguin - purchased at the Puzzle Party from premier Kumiki collector Frank Potts
I am told the Penguin is a fairly rare piece.

Kumiki Monkey

Kumiki Panda - from the Yamanaka Kumiki Works,
in its original package with instruction sheet.

Kumiki Tyrannosaur Kumiki Dragon Bank

Kumiki Rocking Dragon Bank
Kumiki Locomotive
A Kumiki Train
Kumiki Trolley Box Kumiki Trolley instructions
Kumiki Trolley by Shackman
with box and instruction sheet
Kumiki Trolley - Smith
Kumiki Trolley by Smith Novelty Kumiki Trolley - small
Kumiki Trolley
A smaller, narrower version.
Kumiki Locomotive

Kumiki Locomotive
Kumiki Motorcycle - this one is missing a few pieces
Kumiki small Jeep

A huge kumiki Motorcycle, with stand.

Large Kumiki Jeep

Kumiki Pickup Truck
Vintage Kumiki Pickup Truck

Kumiki Tank - Toybox Puzzles distributed by ISHI Press.

Kumiki small Tank
This small Tank puzzle along with the Gun Truck, have acquired a rich patina.
I've shown the markings on the bottom in two orientations since I don't know which is correct.

Kumiki Gun Truck
This "Gun Truck" along with the small Tank, have acquired a rich patina.
Unfortunately my example is missing a few pieces.

Kumiki Rocket

Kumiki Flying Saucer - a simple but elegant design

Kumiki Saturn - I finally found an intact example.
Kumiki Universal Puzzle Set
Wooden Universal Puzzle Set - a vintage set of three space-themed Kumiki puzzles
Complete with box and instruction sheets.

Kumiki Airplane

Vintage Kumiki Aeroplane - Japan

Kumiki Bomber

Vintage Aeroplane Block Puzzle

Kumiki Ship - 2 stacks
Kumiki Ship
Only two stacks.

Kumiki Battleship
Of the Kumiki ships I have, I think this one has the most interesting architecture.
Kumiki Cruiser - Japan
Kumiki Cruiser - a classic vintage puzzle from Japan.

New Kumiki Ship - this example is a modern offering, made from monkeypod rather than Ho wood, including (poorly) photocopied instructions rather than rice paper.
Long Kumiki Cruiser - Japan
Longer Kumiki Cruiser - note the lack of side panels.

Large Kumiki Battleship - I found another very nice vintage kumiki ship -
this seems to be one of the more rare types. It included a box and instructions, both in good shape.

Kumiki Paddlewheeler - Yamanaka Kumiki Works
Here are some group shots of some kumiki ships:
Large Kumiki Battleship with group Kumiki ships - Japan
Kumiki Battlecruiser - Bell
Battlecruiser - a hard (brittle) plastic kumiki-style puzzle from Bell of England
Same architecture as the wooden version.

[134]

Plastic, Metal, and Other Kumiki-Like Puzzles

The 8-Ball puzzle is one of the first puzzles I collected as a kid.
I finally found the five others in what I now know is the Odd Ball series
issued by Norstar Toys Inc. of NY in 1970 (L to R, top to bottom):
Baseball, 8-Ball, Golf Ball, Basketball, Football, Bowling Ball.
8-Ball Odd Ball

Here are the pieces of the Football:

Football Odd Ball pieces

a plastic ball	a newer plastic ball	The "Gold Moon" I got in Japan
Terra-Toys offers a series of four "3D Puzzle" animals in their Wildlife Conservation Collection, made in China from woods claimed to be certified by the Forest Stewardship Council. I picked up a Polar Bear and a Panda. Both have unusual opening tricks - not difficult, but distinct from the typical Kumiki-style animals. There are also a Rhino and a Sea Turtle. The Rhino is very similar to the Nanook Polar Bear.

Geo Australia offers the "KumiKube" puzzle.

Chuck, Woodchuck and Lunatic Burrs

Woodchuck - Pentangle Lunatic - Pentangle The Chuck puzzle, according to Slocum and Botermans in Puzzles Old and New on page 74, was patented by Edward Nelson in 1897 (U.S. Patent 588705 - Nelson 1897). The design was improved and developed by Ron Cook at Pentangle Puzzles. Pentangle offers a series of chuck puzzles - the simplest is the Baby Chuck with 6 pieces. The Woodchuck (shown here) has 24 pieces, the Papa-chuck has 54, the Grandpapachuck has 96, and the Great Grandpapachuck has 150.

Pentangle's Lunatic puzzle, also shown, is a close relative of the Chuck family.

Richard Whiting's website offers a solution to the 24-piece Woodchuck. (The knock-off versions are called "Crystal" puzzles but that is a misnomer.)

Chuck Burr - Colin Gaughran Here is a Chuck burr made from Maple and Walnut by craftsman Colin Gaughran, who has a shop in Lyme, Connecticut.

Papa Chuck - by Pentangle

Here is a Chuck burr in plastic, from Hungary.

Burr - Hungary

Japanese Pagoda (or Crystal) Burrs

These interlocking puzzles are examples of "Pagoda" or "Japanese Crystal" burrs. (Note that the Tower of Hanoi puzzle is sometimes called the Pagoda puzzle, and there are also Kumiki Pagoda puzzles - but here we're talking about another class of burr.) The Pagoda Burr design is easily scalable - the simplest has only three pieces. Larger versions then have 9, 19, 33, 51, 73, 99, and 129 pieces. In general, the n^th degree pagoda requires 2n²+1 pieces.

At the Cleverwood site, they say that the 129 piece is rarely produced since it is considered too difficult. I have not seen any order 9 or 10 (163 or 201 piece) Pagoda puzzles.

Order 'n' 1 2 3 4 5 6 7 8 9 10
Edge Length 2 3 4 5 6 7 8 9 10 11
Pieces 2n²+1 3 9 19 33 51 73 99 129 163 201

You can see the pieces for several sizes of Pagoda puzzle at Ishino's Puzzle Will Be Played... website.

A nineteen-piece Pagoda (and a similar 15-piece puzzle) are described in Wyatt's 1928 Puzzles in Wood on pages 33-37. Plans for a 51-piece Japanese Crystal are given in van Delft and Botermans' 1978 Creative Puzzles of the World on pages 77-79. Slocum and Botermans describe The Great Pagoda puzzle in their 1986 book Puzzles Old and New on page 73.

3-piece Pagoda, edge-length 2
Pagoda size 2 3 piece Lego burr
The 3-piece version requires a rotating piece. I don't have a wooden example, but I made a Lego 3-piece Pagoda Burr, also shown on Brickshelf.
You can see more Lego versions at Maarten Steurbaut's website.

9-piece Pagoda, edge-length 3
Pagoda size 3 Miyako Miyako
The tiny vintage Miyako puzzle I have is a 9-piece pagoda. It does not require a rotation.
The Arjeu CT31 is another example.

19-piece Pagoda, edge-length 4
Pagoda size 4
I have the Arjeu CT1102 Mercurius
The Arjeu CT30 is another example.
33-piece Pagoda, edge-length 5
Pagoda size 5
The Arjeu CT44 is an example.
I got an inexpensive smallish version from an Asian vendor.
51-piece Pagoda, edge-length 6
Pagoda size 6
I have a 51-piece Pagoda issued by Bits & Pieces.
The Arjeu CT80 is another example.

73-piece Pagoda, edge-length 7
Arjeu CT45 73 pc Pagoda
I have the Arjeu CT45
a large wooden 73 piece Pagoda puzzle
99-piece Pagoda, edge-length 8
Superpagoda - Troyer
Superpagoda - made by Henry Troyer.
It is quite large and made from attractive woods.
Check out Henry's Etsy Shop.
The Arjeu CT46 is another example of a 99-piece Pagoda (I don't have it).
Creativecrafthouse.com sells 99-piece and 51-piece versions.
129-piece Pagoda, edge-length 9
Great Pagoda - Cleverwood
Great Pagoda - an edge-9 (129 piece) Pagoda Burr.
Fairly compact given its complexity, but very nicely made.
Purchased from Cleverwood.
Shown with edge-6, edge-5, and edge-8 examples.
I don't know of anywhere else to get a 129 piece pagoda (or larger).

[7]

The Altekruse Puzzle and Variants

In 1890, William Altekruse patented (430502) an interlocking puzzle now known as the Altekruse Puzzle. You can read about the Altekruse puzzle in Stewart Coffin's The Puzzling World of Polyhedral Dissections. The Altekruse is discussed on page 72 in the 1987 Puzzles Old and New by Slocum and Botermans. Edwin Wyatt also discusses this puzzle, calling it "The Twelve Piece Burr" in his 1928 Puzzles in Wood.

The Altekruse uses a set of identical pieces one of which is shown in the patent in Figure 2, and can be made with 12 or 14 pieces. Pentangle offers a 14-piece version called Hybrid, and a 12-piece version called Holey Cross. Many variations have been made.

Wyatt gives solution instructions, shown below. The first step emphasizes the importance of the subtle difference in the arrangement of the two pairs of pieces with respect to their center tabs. In the second step, pieces 5 and 6 should be symmetrical like 3 and 4, while 7 and 8 are parallel like 1 and 2. This allows subassembly 1-4 to slide to the right so that pieces 9-12 can be inserted.

Altekruse solution

Altekruse - Colin Gaughran
Colin Gaughran made this 12-piece version of the Altekruse.
Note the pattern of four blocks on each face. Arjeu CT14 - Criss Cross - Altekruse
Arjeu CT14 "Criss Cross"
This is an example of the 14-piece Altekruse variant.
Note the pattern of five blocks on each face.
Xeons
The Xeon Molecule by Skor-Mor is a plastic, modern-looking version.
I managed to find 3 separate copies - one is all blue, one is red/white/blue, and the third is red/yellow/blue. One of them even came with a solution sheet. On two of them, some of the pieces had broken fins, but the bits were included and I was able to glue them back together. Adams Panel Puzzle
The vintage 12-piece Panel Puzzle by Adams is also a version of the Altekruse. This is also called the "Block Puzzle Senior."
Arjeu CT679 (Ishi)
This is Arjeu CT679 - I purchased it from Ishi back when they offered such things. This variation of the Altekruse puzzle uses single pin/single hole pieces, six left-handed and six right-handed. Stewart Coffin describes this variation in his book, The Puzzling World of Polyhedral Dissections. Frantix
Stewart Coffin developed and licensed the pinned version of the Altekruse puzzle which was marketed by 3M and Avalon Hill and named Frantix. Here are the 12 pieces of the plastic version of Frantix.
[John Rausch's Frantix page]
Giant Steps - Kerry Verne - Sapelle
Kerry Verne made this version of Stewart Coffin's Giant Steps #10 puzzle, from Sapelle. Purchased from CubicDissection. This looks like a pagoda burr, but notice the missing blocks in the inner corners. It is actually an Altekruse variant.

Coordinate Motion Assemblies

In this type of puzzle, several (usually all) of the pieces must be moved in a coordinated fashion to achieve assembly or disassembly.

3-piece Heart Box - Bits and Pieces	Triple Decker - Bits and Pieces	This is called "Iwahiro's Apparently Impossible Cube #1." It was designed by Hirokazu Iwasawa. It was made by Eric Fuller from Chakte Cok wood.
Duodeciburr Designed and made by Vaclav Obsivac Presented at IPP27 by Rick Eason 12 identical pieces	TriKubus by Rik Brouwer Purchased from Bernhard Schweitzer I no longer own this.	This is the Crystal Cube, designed by Bill Darrah. Purchased from Bernhard Schweitzer at IPP 29 in SF. I especially like this design because the pieces are not identical.
E-Box - Vinco A nice little 3-piece coordinate motion puzzle. Purchased from Tim Udall at NYPP 2016.	This is the Dice Box, designed by George Bell [S], with input from Scott Elliott, and printed by Scott. It's not overly difficult, but I think the printed live hinges are cool.
Obtained at IPP31 in Berlin, here is a four-piece Dual Tetrahedron coordinate motion puzzle, beautifully crafted from Walnut, Acacia, Maple, and Plum, from Vinco.		Little Slide Plank Cube - designed by Gregory Benedetti Greg has achieved a very clever dissection of the cube into three similar but different pieces that fit together with coordinate motion. Precision made.
Six Piece Sliding Cube - designed by Gregory Benedetti A coordinate motion puzzle using six similar pieces. Not easy to get started. However, unlike many other coordinate motion puzzles, putting it back together was actually pleasant rather than frustrating.
Viper Cross by Vinco. Six piece coordinate motion puzzle.		Slideways Cube - designed by Ray Stanton made by Pelikan, exchanged by Ray at IPP35.
Slideways Cube - designed by Ray Stanton, made by and purchased from Lee Krasnow. The quality of Lee's 3D prints are outstanding!
The Bow - A beautiful coordinate motion puzzle, made by Bill Sheckels from red zebrawood. Expertly contoured and finished! Check out Bill's Etsy shop Black Dog PuzzleWorks.
Back in July 2019, Ray Swinney, a friend of the late puzzle designer Robert Rose, contacted me - Ray's son had been able to fabricate a limited edition of nice metal coordinate motion burr puzzles. Ray kindly sent me an example - thanks, Ray!
A metal four-piece coordinate-motion Tetrahdron puzzle, from a popular online shopping site. This is a (probably unlicensed) copy of a design by Dr. Bruce Patterson.		Trap Door Octahedron - a three-piece coordinate motion puzzle, by George Bell. Very tricky! Thanks!

Three-Piece Burrs

These are examples of a common 3-piece design known as O-C-C, after the shapes of the three pieces. The OCC design was described by Edwin Wyatt in his 1928 book Puzzles in Wood (pp.24,25) - he called it the Three-Piece Cross; Wyatt gives no history. Hoffmann describes the OCC in his 1893 book Puzzles Old and New in Chapter III No. XXXV "The Cross-Keys or Three-Piece Puzzle" but gives no history. Van Delft and Botermans also describe the puzzle, as "The Wooden Knot," on page 67 of their 1978 Creative Puzzles of the World but again cite no history. See U.S. Patent 4198053 - Rao 1980. According to Singmaster, the Hordern collection contains an instance called "Le Noeud Mysterieux" from circa 1880-1905. It has been produced in wood, and also in plastic as the Triple Cross by Skor-Mor. Here is a link to Jurgen Koeller's page showing the solution. Someone had the idea to notch a knife, fork, and spoon so they could be assembled like the OCC burr.	Only a few other three-piece burr designs can be considered at all well-known. One other common design employs two notched pieces, and a piece with a rounded shaft that allows the piece to be rotated in place. I made a copy from Lego, and posted photos on Brickshelf. This design was also described by Wyatt in Puzzles in Wood, on page 26. This is also the simplest form of a Pagoda or Japanese Crystal puzzle.
Le Noeud Mysterieux - a vintage wooden French boxed puzzle
Tripla - Metallofactura Designed by Andrei Ivanov Among the Top Ten Vote Getters in the 2017 IPP Design Competition
Here is an example of Bill Cutler's GigaBurr design, made by Tom Lensch. (I don't have this.) During 1998-1999, Bill Cutler performed a complete computer analysis of all 3x3x3 three-piece burrs. He found 248,540,275,292 (i.e. almost 250 billion) different designs. There are 80 designs at the highest level, 8, and they come apart in two different ways. Of the 80, there are only 3 that have 9 internal voids - 2 of those come apart in one of the ways, and just one comes apart the other way. Bill named this GigaBurr. The other type is called GigaBurr II. GigaBurr was Bill's exchange puzzle at IPP19.	Here are additional examples I made from Lego: Bill Cutler's Cubie Burr #1 and Cubie Burr #2, both of which require 6 moves to open. These are based on the 3-piece GigaBurr, expanded to a 5x5x5 cube by adding edge and corner pieces. Cutler's 2000-2001 complete computer analysis of all such designs found three different disassembly sequences at the highest level, 6. Cubie Burr #1 was Bill's exchange puzzle at IPP21.
3 Piece Burr (monkeypod wood)
3 Piece Burr Key-o - designed by Osanori Yamamoto produced by Puzzlewood Thanks Chelsea!
The Three Piece Not designed by Frans de Vreugd and made from Sapelle and Padauk by Eric Fuller. Masquerades as the innocent OCC, but it's NOT. Eight steps to remove the first piece.	This is Neptunus from Arjeu (CT1101). It is made of three notched plates.
Triple Play - designed by Jim Gooch and made by Eric Fuller, from Walnut and Redheart. The solution requires an unconventional move, and Eric says some people thought it was an impossible object.	The Schaekel Knot, made of Kingwood, by Tom Lensch, and purchased from CubicDissection. It was designed by Oskar van Deventer.
R. D. Rose - #4 X-Y-Z Burr Three identical pieces that assemble using coordinate motion. This is a nice aluminum example of the design by Wilhelm Segerblom of Wakefield, MA, published in the April 1899 issue of Scientific American magazine.	The Slideways Burr designed by Ray Stanton and made by Eric Fuller, from Curly Maple. The 3 identical pieces assemble with coordinate motion. *Note: this looks like the Improved Segerblom* three-piece burr discussed on Jurg's site. The original design by Wilhelm Segerblom was published in the April 1899 Scientific American, and is described in Slocum and Botermans' Puzzles Old and New on page 66, as well as in the Book of Ingenious and Diabolical Puzzles on page 73.
Tri Again - designed by Frank Potts, and made from Walnut and Maple by Eric Fuller. This actually has six pieces, but they interlace to form the traditional three-bar shape. Magnets hold the pieces in their closed positions.	This is the Yamaosa 3 Piece Burr, designed by Osanori Yamamoto and made by Eric Fuller from Walnut.
Just the Three, designed by Jack Krijnen and made by Eric Fuller, from heavily Quilted Sapelle. A nice sequential level 7.2 assembly - according to Eric, the highest level possible for this form factor.	Three Open Windows, designed by Tom Jolly and made by Eric Fuller, from Bloodwood, Wenge, and Holly.
Invented by Nob Yoshigahara, this little burr is a poseur - read about it on Jurg's site. A gift from Peter Wilshire at IPP-29 in SF. Thanks, Peter!	I got this 3-piece burr, made of acrylic, at IPP 29 in SF. It's called 33E and was designed by Frank Potts.
Cheer - designed by Ronald Kint Bruynseels, issued by Philos. A three piece interlocking puzzle.
Uri Three Bars - designed by Dario Uri Made by Eric Fuller from Wenge and Maple A single Level-10 solution.
Burr Bones - designed by Frank Potts, made by Eric Fuller from Maple and Bubinga [Dis]assemble the three pieces.
Just 3 - designed by Noah Prettyman, made by Eric Fuller from Zebrawood. Three pieces, level 8.4.
Grooved Three Piece Burr - designed by Kouki Kusumi, made by Eric Fuller from Leopardwood.
Several other unconventional designs using three pieces are shown on Ishino's website.

Boxed Burrs / Caged Burrs

This group usually has 4 or 6 pieces, interlocking inside a container. Some have irregular pieces.

Boxed Burr - Tom Lensch
This is a boxed burr I got from Tom Lensch. Each face of the outer box is attached to one burr piece inside the cube. Freeing the key piece requires a trick. The burr pieces used are: #1, #256, #888, #911, #928, and #1024. The box definitely makes it easier to solve, since the faces are distinctly fitted. The mahogany wood is really beautiful. Secret Box (Jeff)
This is a 4-piece burr in a box from Arjeu, variously known as the "Secret Box" or "Pandora's Box" (I also made a copy from Lego). It employs (2x) #792, but the other two pieces have notches where Jurg's system does not allow them (beneath positions 1,4,5, or 8). aluminum Combustion - Bits and Pieces
This is the "Combustion" burr from B and P. My first became hopelessly jammed; I obtained another.
According to Brian Young, both Internal Combustion and Pandora's Box are the same design, by Tadoa Muroi in the early 1990's.

Six piece caged burr
Purchased at a puzzle store in Berlin during IPP31. Six-Piece Framed Burr by miToys - Mr. Puzzle Australia
Six-Piece Framed Burr by miToys
Turtle's Heart - Kotani
Life At 21 - Bits and Pieces
"Life at 21" - Bits & Pieces Burr in a Cube 1
Burr in a Cube #1 by Jürg and Karin von Känel, their exchange at IPP20.
The pieces are { 52, 256, 888/1007, 2x 1024 }.
They describe this puzzle: "There are a few notchable burrs which are level 4 and unique when assembled inside a cube, but they are of lower level and not unique when assembled outside. Burr in a Cube #1 is the one with the fewest internal voids."
Their website has a link to a PDF giving the solution. Hard Core - de Vreugd - BP
This puzzle from Bits and Pieces is called Hard Core and was designed by Frans de Vreugd.
Burr in Cage - Ishino
Burr in Cage 4 12, designed by Ishino
made by Maurice Vigouroux, from Padauk
from the French online puzzle shop Arteludes.com run by Jean-Baptiste Jacquin and Maurice Vigouroux.
Level 4.12.2.1.2.2, unique solution, 9 holes.
Here is a link to the Puzzle-Palace entry for Ishino's Burr in Cage 4 12 from Arteludes. Here is a link showing the pieces.
The pieces are { 52, 256, 768, 1007, 2x 1024 }.
Compare to von Känel's Burr in a Cube #1 above, which has 888 instead of 768.
Quantum Entanglement - Goh Pit Khiam
This boxed 6-piece burr is called Quantum Entanglement. It has a unique level 48 solution. Swiss Cube - von Kaenel U.S. Cube - von Kaenel
The red puzzle is a 3-piece boxed burr called the Swiss Cube. There are two versions - easy and hard - they look the same from the outside, but their pieces are differently notched. I have both.
The red and blue puzzle in a clear cube is called the U.S. Cube. It has six interlocking pieces. All created by Jurg von Kaenel. Inoowoo Cube
Innowoo Cube (?)

Yin Yang - Pelikan
An unusual six-piece burr inside a hollow ball. The Yin-Yang symbols are attached to the ends of the burr pieces.
Purchased from Puzzlewood.de. Nested Burr Four - CubicDissection
Nested Burr Four
CubicDissection
Prisgon - Philos (Goetz)
Prisgon from Philos, designed by Markus Goetz
Purchased in Prague.

Swirls 1 - Cohen
This is Swirls 1, designed by Bram Cohen. Purchased from Bernhard Schweitzer at IPP 29 in SF. Four pieces in a cage - a very difficult puzzle! Choreographed Motion - Roever
Choreographed Motion, designed by Andreas Roever
Purchased at IPP 29 in SF.
The four pieces have angular cuts, and multiple pieces must be moved at once. Clever, and not overly difficult. Nicely made from acrylic. Quintuplets - Gonsalves
This is Quintuplets, designed by Franklin Gonsalves. Purchased from Bernhard Schweitzer at IPP 29 in SF.
Tomtop Ball burr Tomtop Ball burr - pieces
An inexpensive "Ball Lock" - one piece seems needlessly truncated.
"Luban Lock Box"
from China, a boxed burr with 6 pieces.
The pieces are 2x4x8.
BurrTools says this has 98 assemblies but 18 solutions. The highest level is 10.6.1.2.2. Doors and Drawers - Toulouzas
Doors and Drawers - designed by Michael Toulouzas,
purchased from Bernhard Schweitzer
Sticks in a Cage by Tom Jolly - Vigouroux
Sticks in a Cage - designed by Tom Jolly - made by Maurice Vigouroux
The Sonneveld Cubed Burr puzzle, designed by Dic Sonneveld and made by Tom Lensch
3 unusual burr pieces inside a cubic cage - rotations are required to solve.
Made from Shedua, Prima Vera, and Granadillo
Five Sticks 28 - Chomine - Fuller
Five Sticks 28 designed by Stéphane Chomine, made by Eric Fuller,
from Walnut (frame) and Gum (burrs).
28 moves to remove the first piece.
4 in 2 - Chomine - Fuller
4 in 2 designed by Stéphane Chomine, made by Eric Fuller,
from Walnut (frame) and Mahogany (burrs).
14 moves to remove the first piece, 17 for the second.
Rupture - Fast - Fuller
Rupture designed by Dan Fast
made by Eric Fuller
Shake Something - Fast - Fuller
Shake Something - designed by Dan Fast, made by Eric Fuller
from Yellowheart and Chakte Viga with a Walnut box
Extract the four pieces from the box.

Rail Box designed by Yavuz Demirhan,
made by Eric Fuller from Maple, Purpleheart, and Padauk
Level 18
3 Sticks Trapped - Chomine - Fuller
3 Sticks Trapped designed by Stéphane Chomine, made by Eric Fuller,
from Walnut (frame) and Yellowheart (burrs).
Level 12.6.8.
Tribord - Chomine - Pelikan
Tribord - designed by Stéphane Chomine,
made by Pelikan from Mahogany and Wenge
Level 17.3.4
Moonflight - Yamamoto - Fuller
Moonflight, designed by Osanori Yamamoto and made by Eric Fuller, from Walnut, Mora, and Wenge. Level 20.2.5.

Padaung Rings, designed by Alfons Eyckmans and made by Eric Fuller from Tulipwood and Acrylic - it takes 24 moves to remove the first piece.
Zauberflote, designed by Gregory Benedetti.
(See this design at Ishino's site.)
Made by Eric Fuller, from Yellowheart and laser-cut acrylic.
Aramis - Chomine - Fuller
Aramis, designed by Stephane Chomine and made by Eric Fuller, from acrylic and bloodwood. Level 12.11.7.12 solution. Captain - Chomine - Fuller
Captain, designed by Stephane Chomine and made by Eric Fuller, from acrylic and bubinga. 34 move solution. 4 Stick 8 - Worrell - Fuller
4 Stick 8, designed by Frank Worrell and made by Eric Fuller, from acrylic, bubinga, bloodwood, wenge, and ash. Unique level 21 solution.
Worm Inside - Chen - Fuller
Worm Inside, designed by Chi-Ren Chen and made by Eric Fuller, from acrylic and wenge. Quads and Rings 1 - Demirhan - Fuller
Quads and Rings 1, designed by Yavuz Demirhan and made by Eric Fuller, from acrylic, bloodwood, and ash. Quads and Rings 2 - Demirhan - Fuller
Quads and Rings 2, designed by Yavuz Demirhan and made by Eric Fuller, from acrylic, bubinga, and ash.

Carbo Cube designed by Donald Osselaer,
made by Eric Fuller from Bubinga, Maple, and Acrylic
Level 6.2 Gaia Gaia Gaia
Gaia designed by Yavuz Demirhan,
made by Eric Fuller from Walnut, Cherry, Sapele, and Acrylic
Level 11.2 Vortex Vortex Vortex
Vortex designed by Chi-Ren Chen,
made by Eric Fuller from Maple, Bubinga, and Acrylic
Level 21, with rotations
Noncsi - Vanyo - Fuller
Noncsi - designed by Tamas Vanyo, made by Eric Fuller from Bubinga and Carolina Ash.
8 pieces pack into the frame in only one way and in a specific order. Level 2.3.9.7.5.

Boards and Sticks with Frame, designed by Gregory Benedetti.
(See this design at Ishino's site.)
Made by Eric Fuller, from Wenge, Bubinga, and Leopardwood.
Triaxe - Chomine - Fuller
Triaxe - designed by Stephane Chomine, made by Eric Fuller
from Quilted Maple and Bloodwood.
Three burr pieces interlock in the frame at level 24. Triaxe - Chomine - Menold
Triaxe - designed by Stéphane Chomine, made by Brian Menold
from Maple and Wenge
Level 24.2
Vectes/Ghidorah - Demirhan - Eyckmans - Fuller
Vectes / Ghidorah - two designs that share the same cage, made by Eric Fuller
The cage is walnut, the Vectes (longer) pieces are yellowheart, and the Ghidorah pieces are canarywood.
Ghidorah uses the three shorter, distinct pieces and was designed by Yavuz Demirhan. It is at level 22.3.
Vectes was designed by Alfons Eyckmans and uses the three longer identical pieces. It is level 37.2.3.
4 Piece Burr Cube
The Four Piece Burr Cube, designed by Osanori Yamamoto, and made from Curly Maple and Purpleheart by Peter Wiltshire. I really like this design, and the beautiful craftsmanship makes this a much-appreciated one-of-a-kind gift! L in Cage - Demirhan - Menold
L in Cage - designed in 2013 by Yavuz Demirhan,
made from Lacewood and Cocobolo by Brian Menold at Wood Wonders
Free four L-shaped pieces from the cage - level 10.2.2
A substantial size with the cage alone at over 3" tall and about 2.5" square.
Cage for Four Sticks - Chomine - Fuller
Cage for Four Sticks, designed by Stephane Chomine, made by Eric Fuller from Dark Rosewood and Sycamore. Level 24.6.3. Hourglass - Yamamoto - Pelikan
Hourglass
designed by Osanori Yamamoto.
Made by Pelikan.
Remove four U-shaped pieces from a frame.
Purchased from Tim Rowett at NYPP2015.
Ice Pillar - Yamamoto
Ice Pillar - designed by Osanori Yamamoto
Level 30.6.3 - the first of the four pieces won't be coming free from the cage quickly! Tower - Damstra - Pelikan
Tower - designed by Klaas Jan Damstra,
made by Pelikan from Bubinga and Walnut
Level 29.2.9.6.3
Spacemine - Demirhan
Spacemine - designed by Yavuz Demirhan,
made by Eric Fuller from Sapele and Imbuya Two Pairs One - Yamamoto - Pelikan
Two Pairs One - designed by Osanori Yamamoto,
made by Pelikan,
purchased from PuzzleMaster
Burrito - Demirhan - Pelikan
Burrito - designed by Yavuz Demirhan,
made by Pelikan,
purchased from PuzzleMaster Castle Hole - Yamamoto - Pelikan
Castle Hole - designed by Osanori Yamamoto,
made by Pelikan,
purchased from PuzzleMaster

Typhoon S1 by Osanori Yamamoto - made by Maurice Vigouroux
Galaxia - Demirhan - Fuller
Galaxia - designed by Yavuz Demirhan, made by Eric Fuller,
from Jatoba, Cherry, and Walnut. Galaxy Z - Yamamoto - Pelikan
Galaxy Z designed by Osanori Yamamoto, made by the Pelikan workshop, purchased from PuzzleWood.de
Wheel Lock - Tzy Hung Chein - Menold
Wheel Lock - designed by Tzy Hung Chein, made by Brian Menold
from Tambodi sapwood, Redheart, and Maple
Level 15.18.14.4 Dispersion - Chein - Menold
Dispersion - designed by Tzy Hung Chein,
made by Brian Menold
from Redheart, Box Elder, and Ziricote
Level 31.2.4.4 Burrbox 1 - Jolly - Menold
Burrbox 1 - designed by Tom Jolly, made by Brian Menold
from Spalted Beech and Holly
Level 8.6.10.3
Mysterious Galaxy - Yamamoto - Pelikan
Mysterious Galaxy designed by Osanori Yamamoto, made by the Pelikan workshop, purchased from PuzzleWood.de Khamsin - Bergmans - Menold
Khamsin designed by Jos Bergmans.
Four pieces and ring, made by Brian Menold from
Walnut, Maple, Wenge, Redheart, and Yellowheart.
PWBP 9.3.3.3 Ring Lock - Hu - Fuller
Ring Lock - designed by William Hu, made by Eric Fuller
from Padauk, Maple, Walnut, Leopardwood, Yellowheart and Purpleheart
[Dis]assemble the six pieces.
Pink Ivory Ring - Irvine - Lensch
Pink Ivory Ring - designed by Ken Irvine, made by Tom Lensch
from Pink Ivory, Maple, and Walnut.
Stan - Vanyo - Pelikan
Stan designed by Tamas Vanyo, made by the Pelikan workshop, purchased from PuzzleWood.de

Arrow - designed by William Hu
made by and purchased from Pelikan.
Zebrano, Wenge, Maple.
Level 23.14.7
Castle - Chein - Pelikan
Castle designed by Tzy Hung Chein.
Made by Pelikan from Oak and Mahogany. Hive - Eyckmans
Hive designed and made by Alfons Eyckmans, from Padauk, Moabi, and Oak.
Purchased directly from Alfons.
Gates-O - Vanyo - Menold
Gates O designed by Tamas Vanyo, made by Brian Menold
A Box Elder cage with Bambooo pins and 8 identical Wenge pieces.
35 moves to get the first piece out. Trichromat - Yavuz Demirhan
Trichromat designed and made by Yavuz Demirhan
The 7cm cubic cage is Wenge, and there are 3 pairs of pieces, of oak, maple, and padauk.
44 moves to get the first piece out.
Mixed Up - Philos
In Brookline I stopped in at Eureka Puzzles and found
a Mixed Up cube from Philos designed by Ad van der Schagt.
Carambole No. 2 - Demirhan - Menold
Carambole No. 2 - designed by Yavuz Demirhan,
made by Brian Menold,
from Sycamore, Wenge, and Yellowheart. Paquet - Demirhan - Menold
Paquet - designed by Yavuz Demirhan,
made by Brian Menold,
from Red Oak and Yellowheart.
Frisbee - Chomine
Frisbee - designed by Stephane Chomine 2012
made by Brian Menold from Hickory and Wenge. Four pieces plus two plate frame.
PWBP 23.9.2.4.3 Plusminus - Demirhan
Plusminus - designed by Yavuz Demirhan 2012
made by Brian Menold from
Brazilian Rosewood and Canarywood. Three pieces plus frame.
PWBP 6.2.2 Optiborn - Chomine - Menold
Optiborn - designed by Stephane Chomine and made by Brian Menold
from Black Palm, Wenge, and Holly. Four pieces plus frame.
Not listed at PWBP for some reason.
Here is a link to Pelikan's version of Optiborn.
Acomodo - Demirhan
Acomodo - designed and made by Yavuz Demirhan 2016 from wenge and purpleheart. Four pieces plus frame.
PWBP 10.2.2
Visit Yavuz' Etsy Shop Cubozone. Quadrox - Chomine - Menold
Quadrox - designed by Stephane Chomine 2018 and made by Brian Menold
from Padauk and Red Oak. Four pieces plus frame.
PWBP 29.11.11.3
Big Quadrox - Chomine - Pelikan
Big Quadrox - designed by Stéphane Chomine,
made by Pelikan from Wenge, Padouk, Acacia, Purpleheart, and Cherry
Level 29.11.7.3
Think Outside the Box - Jolly - Fuller
Think Outside the Box - designed by Tom Jolly and made by Eric Fuller
from Cherry, Padauk, Maple, Yellowheart, and Purpleheart woods.
Klaas Jan 23 - Damstra - Menold
Klaas Jan 23 - designed by Klaas Jan Damstra,
made by, and purchased from Brian Menold of New Jersey.
Made from Redheart and Yellowheart.
Quadrant 1 - Demirhan
Quadrant 1 - designed by Yavuz Demirhan
made and exchanged at IPP35 by Eric Fuller
Mekaniko, Mekano, Gaveta Cross - Demirhan
Mekaniko, Mekano, and Gaveta Cross
designed, made by, and purchased from Yavuz Demirhan.
Cleverly designed, beautifully made, substantially sized, and reasonably priced.
Check out Yavuz' Etsy site Cubozone.
(Gaveta Cross is not a caged burr.) Gravity - Alkema - Pelikan
Gravity
designed by Tim Alkema
Beautifully made by Pelikan
from Cherry, Wenge, Purpleheart, Acacia, and Padouk
Extract four pieces plus a cube from the sleeve.
Level 14.2.2.2
Simple Puzzle - Damstra - Menold
Simple Puzzle - designed by Klaas Jan Damstra,
made by, and purchased from Brian Menold of New Jersey.
Made from Maple and Wenge. Saturno No. 1 - Demirhan - Menold
Saturno No. 1 - designed by Yavuz Demirhan,
made by Brian Menold from Padauk and Granadillo
Painful - Demirhan - Menold
Painful designed by Yavuz Demirhan
made by Brian Menold
from Canarywood and Redheart
Separate the four pieces
14 moves to free the first piece.

Four in the Vice, designed by Stephane Chomine, made from Silver Ash and Snakewood by Mr. Puzzle Australia.
Exchanged by Frans de Vreugd at IPP32

Two Halves burr by Gregory Benedetti, a caged 3-board burr, made from Ash and Mora, by Eric Fuller.
Regola 4 - Demirhan
Regola 4 - designed and made by Yavuz Demirhan
from Sapelle and Ash
Attis - Smart - Fuller
Attis - designed by Terry Smart, made by Eric Fuller
from Purpleheart and Yellowheart
A six-piece burr in a cage, at level 15.14.4.
Clamped Burr - Kleinwaks - Fuller
Clamped Burr - designed by Logan Kleinwaks
Made by Eric Fuller, from Cherry, Walnut, and Ash
Level 15.3.5
A partially boxed burr - one in a series of increasingly Constrained Burrs including: Bookend (base and 1 side), Cornered, and Looped. Blocage - Chomine - Pelikan
Blocage - designed by Stéphane Chomine,
made by and purchased from Pelikan.
Merbau and Apple woods. Fenced Burr - Demirhan
Fenced Burr - designed and made by Yavuz Demirhan at Cubozone
Snapped Burr - Demirhan
Snapped Burr - designed and made by Yavuz Demirhan
Fossil Burr - Demirhan
Fossil Burr - designed and made by Yavuz Demirhan
from Wenge and Ash woods. Level 12.2.3.2. Fossil Burr II - Demirhan
Fossil Burr II - designed and made by Yavuz Demirhan
from Maple, Wenge, and Padauk woods. Level 9.
Two Burrs in a Corner - Kleinwaks - Fuller
Two Burrs in a Corner - designed by Logan Kleinwaks, made by Eric Fuller, from
Walnut (the box), Goncalo Alves, Bubinga, Cherry, Zebrawood, Masonia, Mahogany, Granadillo, Leopardwood, Canarywood, Sucapira, Padauk, and Purpleheart
Twelve burr pieces pack into the box in only one way, and also form two traditional 6-piece burrs (a level-5 and a level-4) simultaneously in only one way.
Two Burrs in a Basket - Kleinwaks - Fuller
Two Burrs in a Basket - designed by Logan Kleinwaks, made by Eric Fuller
from Peruvian Walnut and Carolina Ash
Tortoise - O�Brien - Pelikan
Tortoise - designed by Alexander Haydon O�Brien
Made by Pelikan, from Dark Oak, Acacia and Wenge
Knot on My Watch - O�Brien - Pelikan
Knot on My Watch - designed by Alexander Haydon O�Brien
Made by Pelikan, from Wenge, Maple, Cherry and American Walnut
Padlock Burr - Alkema - Fuller
Padlock Burr - designed by Tim Alkema, made by Eric Fuller
from Sappy Cherry and Marblewood
Level 24.2.8.
Mini Lock - Lohe - Pelikan
Mini Lock - designed by Christoph Lohe 2018, made by Pelikan
from Ash and Purpleheart. Three pieces and frame.
PWBP 6.7
Spiral Lock - Lohe - Pelikan
Spiral Lock - designed by Christoph Lohe, made by Pelikan
from Purpleheart, Acacia, Wenge, Padouk, Mahogany, Maple and Cherry. Five pieces plus frame.
PWBP 21.3.3.2.2
Trenta - Lohe - Menold
Trenta - designed by Christoph Lohe 2017, made by Brian Menold
from Ash and Mahogany. Three pieces and frame.
PWBP Kubikub 2 - Demirhan
Kubikub 2 - by Yavuz Demirhan Cross 5 - Demirhan - Menold
Cross 5 designed by Yavuz Demirhan
made by Brian Menold
from Canarywood, Walnut and Redheart
Remove five pieces from the frame.
11 moves to free the first piece.
Pox Box - Demirhan - Fuller
Pox Box - designed by Yavuz Demirhan, made by Eric Fuller
from Sapele and Birdseye Maple
Summer - Damstra - Menold
Summer - designed by Klaas Jan Damstra, made by Brian Menold
from Curly Maple, East Indian Rosewood, and Padauk.
Level 14.4.2.
Top - Yamamoto - Pelikan
Top - designed by Osanori Yamamoto, made by Pelikan
from Ash and Bubinga.

Two-Piece Plus Frame (Caged Dancers)

I created this "Caged Dancers" sub-group within Boxed/Caged Burrs, since there seem to be several puzzles where two pieces "dance" or wend their way past each other to be separated from or inserted into a single integral frame piece, and frankly they can blur together, so I wanted to keep track of the different examples. Note that there are other subcategories where either there are more than two "dancer" pieces, or the frame comprises more than a single piece. I particularly like interlocking puzzles that can generate a decent but tractable level of complexity with a minimal number of pieces - and it seems I am not alone, as one member of this group, Identical Twins by Osanori Yamamoto, won the IPP37 Design Competition Puzzlers' Award.

Double UT, designed by Osanori Yamamoto 2011, made by the New Pelikan Workshop, exchanged by Abel Garcia at IPP32
PWBP 16.5
N-One - Yamamoto
N-One - designed by Osanori Yamamoto
Three pieces, level 15.3
Made by Eric Fuller, in Jacaranda Pardo and Bubinga
Columnata 2P3C - Demirhan
Columnata 2P3C - designed by Yavuz Demirhan 2012
PWBP 12.5
Pylon 2P2C - Demirhan
Pylon 2P2C - designed by Yavuz Demirhan 2013
A very satisfying puzzle that was more difficult for me the second time around!
PWBP 9.9
Petit Puzzle - Yamamoto - Lensch
Petit Puzzle - designed by Osanori Yamamoto 2013,
made by Tom Lensch.
PWBP 11.2
Pair Dance - Yamamoto
Pair Dance - designed by Osanori Yamamoto 2013
made by Eric Fuller from Jatoba and Purpleheart
PWBP 14
Just Two In Box - Chomine - Menold
Just Two In Box designed by Stéphane Chomine 2013.
Two pieces and cage, made by Brian Menold from Canarywood and Walnut.
PWBP 11.7
Identical Twins - Yamamoto - Pelikan
Identical Twins - designed by Osanori Yamamoto 2016 -
made by Pelikan from Wenge and Apple
PWBP 6.2 w/ rotation
Winner of the Puzzlers' Award at the IPP37 Design Competition
Lucida - Yamamoto - Lensch
Lucida - designed by Osanori Yamamoto 2016 and made by Tom Lensch
from Walnut and Canarywood
PWBP 10.3 w/ rotation
Slot Machine - Ustjuzhanin - Fuller
Slot Machine - designed by Andrey Ustjuzhanin 2017 and made by Eric Fuller
from Leopardwood and Ash
PWBP 18
Liliput - Lohe - Menold
Liliput - designed by Christoph Lohe 2017
Made by Brian Menold, from lacewood, purpleheart
PWBP 21.3

[11]

Non-Traditional Burrs

This section contains a wide variety of interlocking puzzles in many different forms, but all composed of various notched sticks or plates. The pieces somehow fit together and must be slid to and fro relative to each other until they either come apart or are re-assembled into the intended shape.

Common / Classic Burrs

Here are a few commonly available "classic" burr puzzles many folks will have seen, and have asked me about - usually because they have the pieces but don't know what the intended assembled shape should be. These puzzles often do not have a formal name - they are re-named ad hoc by whoever is marketing the latest iteration - nor do I know who may have designed them.

Classic Six Plank Burr
Four identical pieces, and two special -
note the notched piece, and the piece above it
which has a short "tray."
The holes are optional decoration.

Classic Twelve Piece Burr
Eleven identical pieces and one with a notch.

The Cell
I bought this in a department store in Japan. It was made in New Zealand. It is made from 24 identical pieces similar to the traditional burr piece 256 - but the notch is longer. A fellow puzzler reports that it has been sold with a mouse figure trapped inside. You construct it in two 12-piece halves which are then "screwed" together.

I have seen this called "Prison" or "Twice Six." Twelve pieces - ten identical and two mirror image. The last four get "screwed" in.

Arjeu

These are from the (defunct) French company Arjeu, which put out an extensive line of interlocking puzzles in a wide variety of shapes.
Some are shown under other sections in this website, and some I do not own and show only for reference - such cases are noted.
Arjeu CT14 - Criss Cross - Altekruse
Arjeu CT14 "Criss Cross" (Altekruse)
Arjeu CT16 Arjeu CT-28
Arjeu CT28
Arjeu CT666 (Jeff)
Arjeu CT666
Here is a link to a solution video on YouTube, and another in lower resolution.
Arjeu CT718
This looks like the "Eighteen Piece Double Cross" described by Edwin Wyatt in his 1946 book Wonders in Wood, on page 31.
Arjeu CT752 La Lanterne
From an Ergatoudis auction

Arjeu CT753
This is made from pieces very similar to CT752 - the slots are moved out towards the board ends.
(I don't have this - shown for reference.)
Arjeu CT52 "3 Keys"
This is an unauthorized copy of the van der Poel 18-piece burr.
Arjeu CT117
Known as "3-4-5."

Arjeu CT757 Arjeu CT456 - pieces
Arjeu CT456
15 2x2x12 pieces, to be arranged in a 4x5x6 structure.
Purchased from PuzzleMaster.ca.
More Arjeu, collected here in one place for convenience, though I wouldn't call all of these burrs.
Some of these are shown under other sections in this website, and some I do not own and show only for reference - such cases are noted.
Arjeu CT442 (Ishi $28 1/18/94)
Arjeu CT442 (Colorado) Arjeu CT210 (Ishi $21 1/18/94)
Arjeu CT210 Arjeu CT795 Cactus (Jeff)
Arjeu CT795 (Cactus)
Arjeu CT755 Quadro (Ishi)
This is Arjeu's Quadro (CT755) Arjeu CT1101 Neptunus
This is Neptunus from Arjeu (CT1101). It is made of three notched plates. Secret Box (Jeff)
This is a 4-piece burr in a box from Arjeu, variously known as the "Secret Box" or "Pandora's Box"

Arjeu CT1102 Mercurius Arjeu CT679 (Ishi)
This is Arjeu CT679 Arjeu CT87 (Ishi $37 1/18/94) Arjeu CT87 (Ishi)
This is Arjeu's CT87 designed by Oskar van Deventer.

Arjeu CT5152
aka Achille Arjeu CT45 73 pc Pagoda
Arjeu CT45
a large wooden 73 piece Pagoda puzzle
Arjeu CT109

Burrs that Masquerade as Traditional Six Piece Burrs, and Elaborations

The Missing Notch burr by Stewart Coffin, made from Canarywood, by Eric Fuller. Double Slideways - Stanton - Fuller
Double Slideways Burr - designed by Ray Stanton, made by Eric Fuller,
from Maple, Walnut, and Sapele.
Camouflaged Burr - Askerli - Fuller
Camouflaged Burr - designed by Emil Askerli, made by Eric Fuller
from Cherry and Walnut woods. Level 4.7. Disguised Burr - Askerli - Fuller
Disguised Burr - designed by Emil Askerli, made by Eric Fuller
from Cherry and Walnut woods. Level 7.2.2.
Glued - Benedetti
Glued, designed and made by Gregory Benedetti. Resembling a six-piece burr, this puzzle is composed of six conventional burr pieces that have been glued together in pairs. The puzzle is level 4.3 and [dis]assembly requires a rotation. It is made from Bolivian Santos Rosewood, Kingwood, Tulipwood, Bloodwood, Difu, and "Wood of Jesuit" and is very pretty. It is a nice size - the pieces are 25x25x75mm - and is quite heavy. Q-Burr - Gooch
This is the Q Burr, designed by Jim Gooch, made by Steve Strickland, from Rosewood.
Four pieces, one of which is a cube. Purchased from Steve Strickland's new website (defunct).
Murbiter's Pseudo-Burr - Ramos
Murbiter's Pseudo-Burr - by Primitivo Familiar Ramos, made by Vinco.
Four identical pieces and a unit cube combine to form the familiar 6-piece burr shape.
A kind gift - thanks, Primitivo!
Crenal - Benedetti - Fuller
Crenal - one in a series of "New Old Style" burrs designed by Greg Benedetti,
made by, and purchased from Eric Fuller.
Made from Purpleheart.
Seizaine NOS #7 - Benedetti - Fuller
Seizaine - NOS #7 - designed by Gregory Benedetti
Made by Eric Fuller from Ambrosia Maple
Ordinary Burr - Lensch
Ordinary Burr - designed by Goh Pit Khiam and made by Tom Lensch
from Yellowheart wood with Baltic Birch plywood mazes for strength.
Looks like a conventional six-piece burr, but inside contains maze-following pins. A Mazing Burr - Yananose
A Mazing Burr - designed by Junichi Yananose
Looks like a conventional six-piece burr, but inside contains maze-following pins.

Eight Piece Burr - made by Scott T. Peterson

Augmented Burrs
P Burr P Burr
P-Burr - designed by Junichi Yananose, made by Brian Young from Queensland Silver Ash and Queensland Blackbean
6 pieces, level 18.2 with a unique solution. The pieces { 856/943, 871, 960/992, 1024 } are length 8 and each has a bar attached to each end.
(If you omit the end bars and substitute 911 for 943, you get the pieces used in Bill Cutler's Bin Cross.)
I am proud to say I solved this one from the unassembled state unaided! Stepping Burr - Yananose - Young
Stepping Burr - designed by Junichi Yananose, made by Brian Young at Mr. Puzzle Australia.
Level 10.
Thanks, Chelsea!

Brace Yourself - designed by Frans de Vreugd for IPP33, made by Brian Young at Mr. Puzzle Australia,
from Papua New Guinean Rosewood.
6 pieces form an unconventionally-shaped burr.
Solved this one from the unassembled state!

The Stellated Burr from Primitivo Familiar Ramos of Spain.
Two copies are shown.
Hybrid Burrs

The Switchboard Burr designed by Jim Gooch and made by Eric Fuller mixes pieces from 3 different styles of burr, and its solution employs a move one does not often see. The woods are: Pau Amerillo (the yellow), Wenge (the dark), and Bocote (the brown striped). Mixed Pieces Burr #2 - Frans de Vreugd
Mixed Pieces Burr #2
- designed by Frans de Vreugd.
Purchased from Frans at IPP28 in Prague.
Conjoined Burrs
Cold Fusion - Kleinwaks - Fuller
Cold Fusion - designed by Logan Kleinwaks, made by Eric Fuller, from Walnut, Maple, and Cherry
Four interconnected burrs, level 18.6.8.

Double Kongming Lock

Bill Cutler and Jerry McFarland designs and Related N-ary Burrs

Wausau '81 - Bill Cutler Wausau '82 - Bill Cutler Wausau '83 - Bill Cutler Wausau '84 - Bill Cutler
The four members of the Wausau burr series by Bill Cutler - '81, '82, '83, and '84.
See Allard's blog for a nice review of the Wausau burrs.
S/M24 - Cutler - Fuller
S/M24
designed by Bill Cutler,
purchased from and made by Eric Fuller
from Ash, Padauk, and Purpleheart.
7 moves to get the first piece out.
Visible Burr - Cutler - McFarland
The Visible Burr, designed by Bill Cutler, made by Jerry McFarland, from Cherry, Maple, and Walnut woods.
The Cutler Cube
This is Bill Cutler's 66-piece Cutler Cube. It is a beauty, 100mm on a side, and difficult to disassemble/reassemble.

Binary Burr - Bill Cutler

Binary Pin Burr - designed and made by Jerry McFarland
Ternary Burr - Khiam - Fuller
The Ternary Burr - designed by Goh Pit Khiam, made by Eric Fuller from Walnut and Cherry.
22 pieces, 75 moves to get the first piece out.

Quadlock 1 - Jerry McFarland
The Quadlock 1 is an interlocking burr cuboid puzzle made by Jerry McFarland from Mahogany, Walnut, and Maple, and designed by him in 1992. Purchased from Jerry. It has 19 pieces and is difficult to take apart. It is beautifully finished! You can read reviews here and here.
BurrBlock - McFarland
BurrBlock by Jerry McFarland
One of Jerry's first copies of his new design, which was entered in the 2012 Design Competition.
It's beautiful, hefty, and quite puzzling!
BurrNova - McFarland
BurrNova - designed and made by Jerry McFarland.
"A puzzle that solves itself." While not wholly true, Jerry's novel design incorporates magnets such that at a certain point several pieces move themselves with a satisfying clacking.
BurrNova won an Honorable Mention in the 2017 IPP37 Paris Design Competition.
This version was since re-designated "BurrNova 2D" as Jerry has created a followup he calls BurrNova 3D (aka Magnetic Madness), wherein hides a mermaid awaiting rescue. Magnetic Madness was among the Top Ten Vote-getters in the 2018 IPP38 San Diego Design Competition. Jerry posted a short video of its action.
Kevin Sadler has a very detailed September 2017 post about BurrNova (2D) on his blog, as well as an August 2018 post about the BurrNova 3D (aka Magnetic Madness).

Designs from Yavuz Demirhan

Yavuz Demirhan of Turkey has designed many interesting puzzles of various types, including assembly, sequential assembly, and interlocking varieties. Yavuz has hand-made many beautiful puzzles himself, and his designs have been produced by noted craftsmen. There are examples of Yavuz' puzzles in various subsections of this site - I created this subsection to have a place for Yavuz' general interlocking puzzles I have not categorized elsewhere. Yavuz has an Etsy shop Cubozone. A comprehensive listing of most of Demirhan's designs can be found at Puzzle Will Be Played, where as of this writing in July 2020, there are 572 designs described.

Lion's Claw - Demirhan - Menold
Lion's Claw - designed by Yavuz Demirhan,
made by Brian Menold,
from Bloodwood. Forma - Demirhan
Forma - designed, made by, and purchased from Yavuz Demirhan of Turkey.
Queen Sixteen - Demirhan
Queen Sixteen - designed, made by, and purchased from Yavuz Demirhan of Turkey. Tetradyma 5x5 - Demirhan
Tetradyma 5x5 - designed by Yavuz Demirhan
Capsula Burr - Demirhan
Capsula Burr - designed by Yavuz Demirhan,
made by Eric Fuller from Walnut and Maple
Hedgehog Burr - Demirhan
Hedgehog Burr - designed and made by Yavuz Demirhan
from Sapelli and Maple woods. Level 16.4. Susie Qube - Demirhan
Susie Qube - designed and made by Yavuz Demirhan at Cubozone
Burrcell - Demirhan
Burrcell - designed and made by Yavuz Demirhan
from Sapelle and Wenge
Six burr pieces and 12 identical exterior pieces. Nembus #2 - Demirhan - Menold
Nembus #2 - designed by Yavuz Demirhan, made by Brian Menold
from Canarywood and Maple.
Volantis - Demirhan
Volantis - designed, made by, and purchased from Yavuz Demirhan of Turkey.
Check out what's available at Yavuz' Etsy shop Creacubes.
Transenna - Demirhan
Transenna (improved) - designed and made by Yavuz Demirhan
Allows an alternate assembly, also shown.
Oramagomaburamago - Demirhan
Oramagomaburamago - designed and made by Yavuz Demirhan

Six- (more or less) Board Burrs, Lookalikes, Elaborations

See Ishino's site for a list of six-board burrs.

Chen's Six Board Burr
Designed by Chi-Ren Chen
Level 2.14.12
Made by Eric Fuller, in Walnut, Ash, and African Mahogany Tropical Fish - Chen - Menold
Tropical Fish
designed by Chi-ren Chen, made by Brian Menold
from Redheart and Yellowheart
A six-board burr.
Level 19.5.1.1.2
Tricolore - de Vreugd - Menold
Tricolore - designed by Frans de Vreugd
made by Brian Menold from Padauk, Holly, and Katalox
Level 3.15.11.2 Y6BB1 - Demirhan - Menold
Y6BB1 - designed by Yavuz Demirhan, made by Brian Menold
from Tzalam, Okoume, and Mulberry
Level 3.11.2.3.4
Knotty 6 - Demirhan
Knotty 6 - designed by Yavuz Demirhan
Ambigram Burr - Benedetti
The Ambigram Burr, designed by Gregory Benedetti.
Available from Puzzlewood.de.
Made from Wenge, Padauk, and Robinia.
Thanks to Bernhard Schweitzer and John Devost!

Knotted Burr - Prettyman - Fuller
Knotted Burr - designed by Noah Prettyman
Made by Eric Fuller, from Black Limba
Grooved 6 Board Burr No. 2 - Pluredro
Grooved 6 Board Burr No. 2 - Pluredro. Made from Bubinga and Beech woods. Level 25.2.3.3.
Tomtop 6-piece board burr Tomtop 6-piece board burr - pieces
An inexpensive (and imprecisely made) 6-piece board burr.
This is the same design that appeared in the French Fabbri series.
Here is one of Andrew Crowell's takes on the six piece board burr - this one is called RIPley and in usual Crowell fashion, requires rotations!
Ripley - Crowell - Menold
Made by Brian Menold from curly maple with paduak splines.
RIPtide - Crowell - Menold
RIPtide - a 6-plate burr requiring rotations
designed by Andrew Crowell,
made by Brian Menold
Bedevil - Demirhan - Menold
Bedevil designed by Yavuz Demirhan, made by Brian Menold
from Redheart and Holly
Delight - Chomine - Menold
Delight - designed by Stephane Chomine and made by Brian Menold
from Lacewood and Bolivian Rosewood. X Marks the Spot - Derek Bosch
X Marks the Spot
designed by Derek Bosch
Sequentially interlace the four acrylic pieces
and form the hash shape.
Purchased from Creative Crafthouse.
George Miller Extreme Torture
George Miller made this version of Frans de Vreugd's "Extreme Torture" separated board burr. It takes 28 moves to free the first piece and then 21 more to free the second piece! Here is a link to the solution on George Miller's site.
Here is an article at woodcentral.com by Steve Strickland about making 6-board burrs.

Gordian's Knot - Thinkfun
Thinkfun now offers an inexpensive and colorful version of the Extreme Torture puzzle. They call it "Gordian's Knot" and it includes a step-by-step reversible solution booklet.
You can see a solution on Richard Whiting's site.

Sonneveld 9-piece Board Burr - made by George Miller.
Augmented Board Burrs
Ozone - Ronald Kint-Bruynseels
This is Ozone designed by Ronald Kint-Bruynseels. It is a six-board burr, with a "hook" attached to each piece. It requires 13 moves to remove the first piece, then 11 for the second. Ronald has designed several unusual burr-type puzzles, and you can see many of them at Bernhard Schweitzer's Puzzlewood site. Richard Whiting has put together a nice page at his site where you can read about several other high-level burrs. Plated Six Piece Burr / Around the Bend
This is Frans de Vreugd's design he used for his exchange at IPP25. Frans calls it a Plated Six-Piece Burr. Mr. Puzzle Australia called it Around the Bend. Frans says he developed it while working on Bent Board Burrs. It uses pieces 120, 154, 256, 412, 960, and 1024. Each has a 2x4 unit plate attached to its right end. It is the highest level burr of this type with notchable pieces. It is made from Queensland Silver Ash (the light wood) and Queensland Blackbean.
Dovetail Burr - Bits and Pieces
Dovetail Burr - designed by Frans de Vreugd
Issued by Bits & Pieces
A single solution, at level 6. Based on Yananose's 6-board burr.

Zig Zag Knot - Thinkfun
The Zig Zag Knot, from Thinkfun.
This is a nice plastic mass-produced version of Ronald Kint-Bruynseels' 2003 design he called "ZeeZee ZedZed" - see it on Ishino's site.
Thanks to Tanya Thompson!

Twin Board Burr - Dawir

A Burr Puzzle Parade

Here is a link to a stop-motion video of several of Mr. Puzzle Australia's puzzles assembling themselves, on YouTube.

These small but elegant burrs are made from a special plywood, from Pacific Puzzle Works.

Knot Mass 36, designed by Oskar van Deventer. This instance is pretty small, at 36mm. It's made from a 5-ply maple core / maple-top hardwood laminate.
Tubular Burr Box (aka Space Invaders), designed by Ronald Kint-Bruynseels. This instance is pretty small, at 36mm. It's made from a 5-ply cherry / maple-top hardwood laminate.
Oskar's Egg
A 3-piece ball inside a 2-piece egg. How does it come apart?
These are members of the "Quad Squad" family of burrs with interchangeable pieces, from Viktor Genel...

Quadrocube - Viktor Genel
QuadroPrizm - Viktor Genel
Long-Beamed Star - Viktor Genel
Kuball - Tom Lensch
The Kuball,
a 3-piece puzzle designed by Viktor Genel. Made by Tom Lensch. See the pieces at John Rausch's PuzzeWorld.
The burrs below are from a variety of sources...
Easy Livin' - Ronald Kint-Bruynseels
Easy Livin' designed by Ronald Kint-Bruynseels
Purchased from Bernhard Schweitzer at NYPP 2008
This is notable because a copy sold for $11,111 in one of Nick Baxter's auctions!

William Waite's Stellar Burr
Rojo
From Davan's, a Rojo

"Numero Caro"
This is an Asian copy of Oskar van Deventer's Knot 12.

T Time - Davans
Maruca - Davans
Zinato - Davans
Die in Prison - Eric Fuller
Die in Prison (with a central puzzle box), designed by Ronald Kint-Bruynseels and made by Eric Fuller. The six pieces are made of Bubinga, and the central cubic box is made of Yellowheart.
This is Luxemburr, designed by Matti Linkola, exchanged at IPP16 - made by Eric in Yellowheart and Walnut.
Lassen Risti - made by Eric Fuller
RD001 - CubicDissection
RD001
Designed by Ronald Kint-Bruynseels and made by Eric Fuller. Gum wood and Ipe. Ribbon Puzzle - Jolly - Fuller
The Ribbon Puzzle, designed by Tom Jolly, made by Eric Fuller from Chakte Cok and Zebrawood - six pieces that form the 3-piece burr shape.

Anderson's Delusion - CubicDissection
Anderson's Delusion
Designed by Ronald Kint-Bruynseels. Made by Eric Fuller from Gum wood and Rosewood.
ISBR x 5 - Uyematsu
ISBR x 5 - designed by Mineyuki Uyematsu
Made by Eric Fuller, from Yellowheart
This is the Tornado Burr designed in 2007 by Junichi Yananose,
made by Eric Fuller from Padauk wood.
Eric says, "This is one of the most difficult puzzles I've ever made.
They are extremely time consuming to make, requiring many specialized jigs.
I doubt I'll be making these again!"
This burr, with its unusual and interesting movement, won an Honorable Mention award in the 2007 IPP Nob Yoshigahara Design Competition.

Here is the Tornado Burr partially disassembled, into two halves:

Band Cube - Hu - Fuller
Band Cube - designed by William Hu, made by Eric Fuller,
from Bloodwood and Acrylic.
Although it looks like a caged burr, of its seven pieces, all three of the plate pieces are open, not rings. See Band Cube at Puzzle Will Be Played. Claw 3 - Eyckmans
Claw 3 - designed by Alfons Eyckmans,
made by Eric Fuller from Grandillo and Sapele
Sweet 16 Burr - Krijnen - Fuller
Sweet 16 Burr - designed by Jack Krijnen, made by Eric Fuller Rar - Vanyo - Fuller
Rar - designed by Tamas Vanyo, made by Eric Fuller
from Maple and Chakte-Kok woods. Level 9.15.1.6.
Accordion 3.5 - Hu - Fuller
Accordion 3.5 - designed by William Hu, made by Eric Fuller,
from Chakte Viga and White Oak. Amatores - Eyckmans - Fuller
Amatores - designed by Alfons Eyckmans, made by Eric Fuller,
from Maple and Walnut. Six Stick Burr - Hu - Fuller
Six Stick Burr - designed by William Hu, made by Eric Fuller,
from various woods.
Boron - Osselaer - Fuller
Boron designed by Donald Osselaer
made by Eric Fuller Gobi - Eyckmans - Fuller
Gobi designed by Alfons Eyckmans
made by Eric Fuller
Chicken Puzzle designed by Olexandre Kapkan
made by Eric Fuller from Yellowheart and Cherry

Double Knuckles Drueke P24 Marian's Puzzle
P24 Marian's Puzzle - Drueke
You can see a solution at Richard Whiting's site.
Karin's Outline Burr

Sliced Burr - Philos
Vesa Burr Simple - Philos
- designed by Vesa Timonen for IPP21.
A gift from Bernhard - thanks! I found Linking Squares from Philos at The Games People Play.
Linking Squares - Philos
Linking Squares consists of 12 pieces with embedded magnets, that must be constructed into an octahedral shape composed of three interlinked rectangles. It was designed by J. Verhoeff.

I found Sheffield Steel 6BB from Philos at The Games People Play.
Sheffield Steel 6BB - Philos
Sheffield Steel 6BB was designed by the prolific Ronald Kint-Bruynseels - it is a six-piece burr at level 17.14.5.2.3 (see the pieces at Ishino's site; Richard Whiting describes the puzzle on his site, and gives a solution).
Open Cube - Kreveld - PuzzleWood
The Open Cube, designed by Marc van Kreveld and Theo Geerinck, produced by PuzzleWood Apple - Yamamoto - Pelikan
Apple - designed by Osanori Yamamoto, made by Pelikan.
A PuzzleMaster exclusive.

The Blitz - Mr. Puzzle Australia
Seems similar to the Saturn shown at Philippe Cichon's site.
Here is Sonneveld's Illegal Burr - Tom Lensch made it. It's "illegal" because a rotational move is required. Twisty - Derek Bosch - made by Tom Lensch
The Twisty Burr, designed by Derek Bosch and made by Tom Lensch. Purchased from Tom at NYPP 2008.

The Boston Tea Chest, from Mr. Puzzle Australia. I have one of their Craftsman Range examples in Australian Flooded Gum wood. Six pieces, with a two-step internal locking mechanism. A traditional burr-solving computer program won't help you with this one. Decemburr - Mr. Puzzle Australia
Decemburr - Mr. Puzzle Australia
A 12-piece, level 13 burr designed by Goh Pit Khiam in December 1999 without the use of a computer. Imagin coated burr
This puzzle from Imagin is a knock-off of von Kaenel's Coated Burr idea.
You can see a solution on Richard Whiting's site.
4-piece burr - Schweitzer
TriRods by Serhiy Grabarchuk - from Bernhard Schweitzer

Bombay Co. Angles and Edges

Yananose 2x3 Type 0
Doublecross - Bits and Pieces
Double Cross - B&P Coming of Age - Brokenshire IPP27
Coming of Age - designed and made by Vaclav Obsivac
Presented at IPP27 by Laurie Brokenshire
Six pieces made from every possible combination of 3 (out of 18) 1x1x5 Walnut bars, plus 8 1x1x1 blocks. The right-hand picture shows the puzzle properly assembled.

QED - Pentangle Mercury Star pieces
This inexpensive Samanea (Monkeypod / Raintree) wood 12-piece burr was sold as the "Mercury Star" but it is a shrunken copy of Akio Kamei's Box and Cage design, without the box. Micro Burr - Waite - Boardman
The Desert Rose micro-burr, designed by William Waite and made by Allan Boardman, who is well-known for crafting microscopic puzzles. It's only 1/2 inch across! Made from walnut and masur birch. Purchased from William at IPP 29 in SF.

Flange 99A, designed by Tom Jolly.
Purchased at IPP 29 in SF.
Laser-cut. Six pieces, only two identical. 8 moves for the first piece.
Flange 77A, designed by Tom Jolly.
Purchased at IPP 29 in SF.
Laser-cut. Six pieces, all identical. 4 moves for the first piece.
Wooden Burr
"Knobbly Burr"
designed by Dic Sonneveld
made by Brian Menold

Snookstick / Starburst - Constantin - B & P
Snookstick (aka Starburst)
designed by Jean Claude Constantin
issued by Bits & Pieces, as Starburst Timonen Burr - Vesa Timonen
In CFF #84 March 2011, Vesa Timonen published an article "A Travelogue to My Puzzle Designs" where he describes the genesis of several designs including the 1998 6-piece Timonen's Burr.
456 Burr
Almost identical to the Arjeu 456 Burr
(I don't have this - sold at NYPP2012.)
Tomtop Heart to Heart burr
Heart to Heart
This is similar, but not identical, to Timonen's Vesa Burr. Knot - Steve Kelsey
A six-piece "knot" laser-cut by Steve Kelsey. Thanks, Steve! Nur Mut - Strijbos
Nur Mut from Wil Strijbos
(Pic from G.S.)
36 Piece Burr - Vigouroux
36 Piece Burr - designed by Jacques Frossard, made by Maurice Vigouroux
This has only eight holes inside. It has one solid key piece, but without using piece coloring constraints, even BurrTools cannot solve it!
Burr Cube by unknown designer - made by Maurice Vigouroux
from Caroline (Loblolly) Pine
Phelan
Phelan, designed by Alfons Eyckmans.
A non-traditional 18-piece burr,
made by Maurice Vigouroux, from Walnut.
Purchased from the French online puzzle shop Arteludes.com run by Jean-Baptiste Jacquin and Maurice Vigouroux.
Ishino shows the pieces, and indicates Phelan is level 17.1.16.8. 5.16.2.8... Vinco 4 Piece Burr - Menold
Vinco 4 Piece Burr
made by Brian Menold

Hyperboloid Burr, designed by Oskar van Deventer and Naoaki Takashima, made by Kanagawa Toy Co. Ltd., exchanged by Naoaki Takashima at IPP32
John Rausch calls this one the 12 piece Twist Burr, and lists the designer as unknown. My copy is a cheap one from Asia.

IPP Burr - Mr. Puzzle Australia
Triade
Triade, designed and exchanged by Andreas Röver, made by New Pelikan Workshop
Brandenburg Gate
designed by Jos Bergmans
requires rotations
produced by Puzzlewood.de
Burr with Washington Monument
Dragon Puzzle with Washington Monument, designed, made, and exchanged by Zandraa Tumen-Ulzii at IPP32
Knobbly Box, designed by Oskar van Deventer, made by Tom Lensch, exchanged at IPP32 by Rob Jones Lancelot - Chomine - Pelikan
Lancelot - designed by Stephane Chomine,
made by Pelikan,
purchased from PuzzleMaster
SIXI Cube - Vinco
SIXI Cube by Vinco. Assemble the six unique pieces. A nice sequential interlocking puzzle.
CEI Burr - Benedetti
CEI Burr - designed by Gregory Benedetti
12 unusual pieces. Disassembly appears easy at first, but beware!
From Bernhard Schweitzer at Puzzlewood.de. Thanks, Bernhard!

3-Board-Burr Quartet - designed by Mineyuki Uematsu
Purchased from eBay seller Cu-Japan
By George Burr - George Syriaque
The By George Burr - designed by George Syriaque in 2011,
and entered in the 2012 IPP Design Competition.
Its six unusual pieces serially interlock.
George kindly sent me a prototype made by Brian Menold - thanks, George!

Colin Gaughran's 12-piece Burr
I had the opportunity to visit Colin's workshop in Lyme and we had a fun discussion about puzzles and puzzle-making.
I saw several works in progress destined for various collectors.
Colin was kind enough to give me this 12-piece burr he designed and made from cherry wood. Thanks, Colin!
While taking inventory in one of my storage cabinets I re-discovered a puzzle I didn't recognize, disassembled in a bag.
I posted a photo of one of the 12 identical pieces to some online forums and asked for help identifying the puzzle.
Cubion - Unknown craftsman
Several puzzle-friends responded (thanks!), and John Devost came through,
suggesting the Cubion designed by Philippe Dubois.
(Also sometimes spelled Coubion.)
Cubion at John Rausch's site, Coubion in Jerry Slocum's collection, Cubion in Tamura's collection,
Cubion in 1999 Baxter auction where lot d7 sold for $93, Cubion in 2007 Baxter auction where lot 771 sold for $525,
Cubion in 2011 Baxter auction where lot 2242 sold for $325.
The Coubion is shown in Slocum's 1994 The Book of Ingenious and Diabolical Puzzles on page 75.
Based on the references and images we found online I was able to reconstruct my copy.
Cubion - Unknown craftsman

Cubion designed by Philippe Dubois, unknown provenance
It fits together albeit with lots of slop. The relatively soft wood makes it easier to "squish" the pieces into place.
The notches are not precisely cut and the resulting fit is imperfect but I cannot fathom any other
better configuration of these pieces with their peculiar cuts. I do not know who made it - it was part of a group
of wooden puzzles of unkown provenance in an auction lot I won back in December 2007.
Crudely made but I give the maker props for even attempting it since the necessary angles seem so obscure!
I wonder how many Cubions are out there?
Had I reviewed my old What's New pages in the first place,
I would have found this photo I posted back in December 2007 of the assembled form...
Cubion - Unknown craftsman
But I still wouldn't have known the name of the puzzle.

Brackets Burr - Chomine - Menold
Brackets Burr designed by Stéphane Chomine.
Six pieces, made by Brian Menold from Redheart and Wenge.
Vauban H5 - Chomine - Pelikan
This is the Vauban H5 designed by Stéphane Chomine
and precisely made by Pelikan Puzzles from Bubinga and Maple. Four pieces.
Smart burr designed and made by Alfons Eyckmans
from Itauba and Wenge woods
15 pieces, level 24.7.1.1. 4.1.2.3.1. 4.5.4.2
I like it because of its 'S' theme!
Thor's Hammer - Baumegger - Pelikan
Thor's Hammer
designed by Stephen Baumegger, purchased from and made by Pelikan, from Maple and Oak. Covalent - Vanyó - Pelikan
Covalent
designed by Tamás Vanyó, purchased from and made by Pelikan, from Maple and Purpleheart. Block - Baumegger
Block - designed, made by, and purchased from Stephan Baumegger of Austria.
Made from Wenge, Bubinga, and Maple. Level 7.2.2.2
See more of Stephan's designs at his Facebook page Puzzleisure.
Really Bent Board Burr - Bosch - Heyns
Really Bent Board Burr - designed by Derek Bosch,
made by and purchased from Johan Heyns of South Africa.
Made from Pau Marfim (light) and Mansonia woods with black Ebony feathers.
Johan supplies a lovely stand as well.
You can contact Johan on Facebook with your requests. Cubic Burr - Jolly - Udall
Cubic Burr - designed by Tom Jolly
made from Red Meranti and exchanged at IPP35
by Tim Udall

Six Piece Open Drawers - real name and designer unknown to me. Sorcerer's Apprentice - Baumegger
Sorcerer's Apprentice - a novel burr designed and made by Stephan Baumegger
Crosscut - Fast - Pelikan
Crosscut - designed by Dan Fast
made by and purchased from Pelikan.
Cherry and Wenge.
Level 13.2
Hug - Eyckmans
Hug - designed and made by Alfons Eyckmans
from Vitex and Padauk
Level 19 Venus - Eyckmans
Venus - designed and made by Alfons Eyckmans
from Ash and Purpleheart
Level 16 Venus 4 - Eyckmans
Venus 4 - designed and made by Alfons Eyckmans.
I've managed a partial disassembly - shown in the background is
an original Venus also from Alfons.
Infinity - Eyckmans
Infinity - designed and made by Alfons Eyckmans
from Ipe, Oak, Okan
Level 25 Simple Sharp - Chomine
Simple Sharp - designed by Stéphane Chomine
Forgotten Piece - designed and made by Marcel Gillen
exchanged at IPP35 by Tania Gillen
Disassemble the burr and reassemble with the extra piece inside.
Kaon - Einfeld - Fuller
Kaon - designed by Duane Einfeld, made by Eric Fuller
from Sapele and Padauk
Six pieces form the shape of the classic OCC burr.
Coniburr - Alkema - Fuller
Coniburr - designed by Tim Alkema, made by Eric Fuller
from Ash and Padauk.
Four outer pieces and four inner burr-like sticks. Level 16.
Recede - O'Brien - Pelikan
Recede - designed by Alexander Haydon O'Brien, made by Pelikan
from Wenge and Cherry.
Coriolis - Pauwels - Pelikan
Coriolis - designed by Lucie Pauwels, made by Pelikan
My copy is made from Maple and Walnut. Silene - Eyckmans - Menold
Silene - designed by Alfons Eyckmans
Made by Brian Menold, from redheart, katalox
Pinco - Cubukcuoglu - Fuller
Pinco - designed by Erhan Cubukcuoglu
Made by Eric Fuller, from Walnut, Leopardwood, Paduak, Canarywood, Maple, Tamarind, Cherry
Pisa #2 + Cubin Burr - Yananose
Pisa #2 + Cubin Burr - designed by Junichi Yananose
Rota # - Pauwels - Pelikan
Rota # - designed by Lucie Pauwels, made by Pelikan.
Robrecht 02 - Louage
Robrecht 02 - a burr designed by Robrecht Louage, from PuzzleWood.de.
Six pieces, one solution, at level 14.4.2.
Thanks, Chelsea!
Burr Lock E - Lohe - Crowell
Burr Lock E - designed by Christoph Lohe,
produced by Andrew Crowell
Moai's Tomb - Crowell
Moai's Tomb - produced by Andrew Crowell

Bison - Krijnen - Pelikan
Bison - designed by Jack Krijnen, made by Pelikan.
Christmas Tree - Baumegger - Pelikan
Christmas Tree - designed by Stephan Baumegger, made by Pelikan.
Japanese Wood Joint Burr - de Vreugd
I long admired and have now found an example of the Japanese Wood Joint Burr, designed by Frans de Vreugd and exchanged by Frans at IPP19 in London.

I learned about five inexpensive wooden puzzles produced under the label "Confusion Contemporary Puzzles" by The Lagoon Group. I purchased mine at Mind Games in the UK.

Trilogy
aka "Three Open Windows"
(made by Eric Fuller)
Designed by Tom Jolly

Squarrel
Designed by Ronald Kint-Bruynseels
See it on Ishino's site

Mental Block
Designed by Rick Eason
aka the Twenty Cube

Caged Knot
Designed by Tom Jolly
See it on Ishino's site

Alcatraz
Designed by Ronald Kint-Bruynseels
aka Die in Prison #2
See it on Ishino's site

Non-Traditional Burrs in Plastic or Metal

Aluminum H-Burr
This is Junichi Yananose's H-Burr, made in aluminum and purchased from Torito.
Cold Fusion, designed and exchanged at IPP32 by Oskar van Deventer, made by Shapeways Kaiyue Ball Burr
Kaiyue Ball Burr (Kong Ming Lock 30394)

Four-piece red weave
The Kray Twins designed and 3D Printed by Steve Nicholls.
This unusual six-piece burr was Steve's IPP34 exchange gift.
Steve kindly sent me a copy - thanks very much, Steve! Triburrlism - Nicholls
Triburrlism - designed, 3D printed,
and exchanged at IPP35 by Steve Nicholls.
Assemble the three pieces so the result fits in the container.
Slida Slida
Slida - Slida website
Colorful but simple.
Cube Ball - Bell
Cube Ball - by George Bell at PolyPuzzles
Form a cube from three 3D printed pieces.
Four Piece Cube - Sonneveld - Krasnow
Four Piece Cube - designed by Dic Sonneveld,
made by Lee Krasnow from various metals. It's tiny!

Randy's Cube - designed by Randy Pearson
Entered in the 2012 IPP Design Competition as "Pearson Puzzle Pieces" - 6 pieces form a cube.
Purchased from e3cubestore.com

The Arch Burr in aluminum, from Bits and Pieces. Designed by Oskar van Deventer.
Six pieces, square in cross-section, but curved. The pieces can be interlaced to form two "traditional" (but curved) six-piece burrs simultaneously, at the ends of the arches.
There is more of Oskar's genius in the Arch Burr than may at first be apparent. The two burrs aren't exactly equal. All the pieces are symmetric in that the "traditional" burr piece that exists on each end of an arched piece is the same, except for the smallest silver piece (middle right in the photo of the pieces). On that one, the pieces on the ends are mirror images!
Using my ID scheme, the large black piece at top left is a 1024/1024, the bottom left black piece is 52/52, and the upper right black piece is the key 1/1.
The silver pieces on the left and in the lower right are both 1024/1024, but the right middle silver is 824/975.
Oskar has realized that the two traditional six-piece burrs { 1, 52, 824, 3x1024 } and { 1, 52, 975, 3x1024 } can be juxtaposed in this arched configuration allowing the shared key to be slid into place simultaneously!
Another note - when you remove the key and glance inside you will see that there is a unit cavity on each end - neither burr is truly "solid" - each has one hole that could have been filled with an extra unit cube. If the large silver piece, instead of being 1024/1024, was 960/992, the burrs would be solid and I believe could still be constructible in this dual configuration. However, the simplification of this piece by the removal of those "fingers" no doubt improved durability and reduced manufacturing complexity and cost.

Dodecafé - Brouwer
Dodecafé - Rik Brouwer
Purchased from Rik's Shapeways shop.
Difficult to assemble and even more difficult to take apart.

Here is a set of burr-type plastic puzzles I bought in Japan - they are members of a "Family:"

Boy

Papa

Lady

Brother

The Dollar Tree store offered several puzzles in a series called "3 Dimension" including:

Fancy Square

Knot

"Stack Cubes" (A Kumiki Cube)

Krasnow's Barcode Burr

Barcode Burr designed by Lee Krasnow
3D printed by Stephen Miller

Barcode Burr - a beautifully produced 3D printed version
of Lee Krasnow's famous puzzle.
Check out Lee's Etsy shop Pacific Puzzleworks.

I also purchased the Barcode Burr Master Expansion Set. The Master Set includes:

(6) piece bodies (enough for one full assembled cube puzzle)
(18) insert attachment screws (6 extras in case you lose any)
(1) hex wrench
(12) TCB orange maze inserts (ternCode Burr)
(12) QCB yellow maze inserts (quadCode Burr)
(12) SCB red maze inserts (superCode Burr)
(12) CCB blue maze inserts (coordiCode Burr)
(2) white maze inserts (ExtremeTortureCode Burr)

I also purchased further expansion piece sets for the Barcode Burr - CrossCode Burr (XCB) Master Set (white, 4 puzzles),
GreenCode Burr (GCB) Master Set (green, 4 puzzles), PurpleCode Burr (PCB) Master Set (purple).

Crosscode Burr Master Set (white) Greencode Burr Master Set (green) Purplecode Burr Master Set (purple)
I skipped the GoldCode Burr Master Set based on its description - "Additional sections of maze path on the insert pieces necessitated decreasing the size of the dowel pin hardware and corresponding maze path width. Much patience and dexterity is required to successfully manipulate these puzzle pieces through their solution sequence without jamming up the pieces." I doubt I'd have the patience.
Of the PurpleCode Burr (PCB), Lee says, "My goal in designing the PCB was to have a good mix of coordinate motion moves and linear moves, with a long and complicated solution path, yet with as much symmetry as possible, and having a somewhat logical progression of piece movement. If the SuperCode Burr (SCB) and ExtremeTortureCode Burr (ETCB) were too much chaos for your taste, then hopefully the PCB will be just the right amount of challenge."

Interlocking Poly-cube Assemblies

Scott T. Peterson is a talented craftsman who produces high-quality limited editions of puzzles in fine woods.
See his website polyhedralpuzzles.com; and info at CubicDissection.

Scott made a few instances of my 2 N's Cube design. Scott has devised an attractive coloring scheme for the cube and made me the examples shown below -
the first in Bocote and Yellowheart, and the second in Kingwood and Holly. (I have since traded the Kingwood instance.)

2 N's Cube - Bocote and Yellowheart - Scott Peterson

2 N's Cube pieces - Bocote and Yellowheart - Scott Peterson

2 N's Cube - Kingwood and Holly - Scott Peterson

I would rate the 2 N's Cube of medium difficulty - it shouldn't take long for an experienced metagrobologist to solve it,
but I think it presents a good challenge for the casual puzzler, particularly if one starts with it disassembled and hasn't seen the assembled arrangement.
The design is the product of a search "by hand" (i.e. without a computer) for a selection of non-planar pieces formed from
two n-tetrominoes each that would allow interlocking assembly into a 4x4x4 cube.
My "theme" was the frequent mis-spelling of my last name, which has two n's. I was pleased to discover an arrangement that used four pairs of pieces -
thusly again doubling the double-n theme - and yet assembled in a way that was not completely symmetric.

Scott's tolerances are so accurate that when I first received the cubes, I had trouble finding the disassembling moves!
Naturally, wood tolerances vary with humidity, but Scott's pieces are very nicely made.

Scott has made copies of my 2N's Cube No. 5 - he designed a very nice pattern based on the "five" theme (each face has five contrasting cubes), and made these two examples -
the first from Ziricote and Orange Osage, and the second from Yellowheart and Wenge. Thanks, Scott, they're beautiful!

The No. 5 design is the result of a computer-assisted search I did (using Andreas Röver's wonderful BurrTools program),
trying to find a better design than the No. 1 I designed originally by hand.
I don't think any of the designs I found by computer topped the No. 1, but of them, No. 5 is my favorite - it uses eight different pieces as opposed to the four pairs in the No. 1.
I think No. 5 is more difficult to assemble, too.

At IPP28 in Prague, Bernhard Schweitzer had a nice surprise for me - he presented me with a copy of my 2 N's Cube No. 5 that he had made - I believe the wood is Meranti. Thanks again, Bernhard!

2N's Cube No. 5 - made by Bernhard Schweitzer

The French puzzler Guy Brette also made a copy - see a video on Guy's website.

These are from Pentangle - all very nicely made:
The Wookey Hole	Mayer's Cube I credit (blame?) Mayer's Cube with getting me moving along on my collection.	King's Court

The Juha #6 cube by Juha Levonen
(Ishino shows other Levonen designs)

The Noris Cube designed by George Pfaffinger, made by Philos, purchased from Cleverwood (discontinued).

The nine-piece Improved Mehandros Cube by Michael Toulouzas of Greece. Purchased from Bernhard Schweitzer.

Three Trapped Sages - designed by P.F. Ramos and Rafael Abad
Purchased from Puzzlewood.de.
This was entered in the IPP 2006 Design Competition.
Maneuver the three maple pieces free of the frame.

Barb's Cube - John Devost
A miniature 3D print from Shapeways
Thanks, Brett!

Don's Dilemma - Don Kuchen - Wood Wonders

Don's Dilemma - designed by Don Kuchen, made by Brian Menold at Wood Wonders, from Yellowheart and Purpleheart

This is a version of Trevor Wood's Holey Squares Cube puzzle, made by Eric Fuller. It is made from Leopardwood and Honduras Rosewood.

From William Waite, the Literal Lateral Slide.

Philos - Confusio Neu - Pfaffinger
Confusio (Product No. 6170), from Philos.
Designed by Georg Pfaeffinger.
Made from Schima, Hevea, and Samena woods.
Form a 5x5x5 interlocking cube from 9 pieces.
Purchased at The Games People Play.

Waite's Wonder
A 4x4x4 cube made of only five pieces that fit together nicely and ingeniously.

Six Pack, designed by Jim Gooch and made by Steve Strickland from Mahogany, Red Oak, Padauk, Bubinga, Walnut, and Pecan.
Six interlocking pieces.

Reunification - Bram Cohen
Purchased from PuzzleWood at IPP31 in Berlin

I received Tango, designed by Jeff Namkung, from PuzzleWood.de. It is nicely made, from Maple and Walnut woods. Five pieces form a 4x4x4 cube, with some holes. Like many of Jeff's designs, Tango requires rotations of pieces on [dis]assembly. Thanks, Bernhard!

The Century Cube II - a 4x4x4 cube composed of five serially interlocking pieces. A nice design that yields to logical thinking.
A copy of Juha A. Levonen's "Juha's No 2."

The (Count Your) Blessings Cube - six interlocking pieces.
The pieces occur in three mirrored pairs.

The Ramube Octahedron designed by Ramu Kaminoff in 2008 and exclusive to Creative Crafthouse. Eight complex pieces and 2 balls locking things up inside. Dave says, "This is in my opinion our MOST difficult puzzle. It is difficult for me to imagine anyone solving this without use of the provided instructions."

8 Plaques designed by Stephane Chomine
made by Brian Menold
Looks like a Snafooz-type cube, doesn't it?
That is, until you realize there are eight pieces rather than six!
I am not going to show you the assembled cube,
since the image gives too many hints.

Slow Waltz - designed by Jeff Namkung
Made by Eric Fuller, in Canarywood and Cocobolo.

Halny - designed by Jos Bergmans and made by Brian Menold
from Black Palm, Holly, Olivewood, Canarywood, Bocote, and Lacewood.

Two Wheeled Cube - designed by William Hu,
made by Bernhard Schweitzer

Danse Macabre - designed by William Hu,
purchased from Bernhard Schweitzer

Chain - designed by William Hu,
gift from Bernhard Schweitzer - Thanks, Bernhard!

Marin - designed by Jos Bergmans,
made by Brian Menold from various woods

Repair the Cube - designed by Andrey Ustjuzhanin, made by Eric Fuller
from Wenge and White Oak - Level 11.10

Wedlock - designed by Laszlo Molnar, made by Brian Menold

Impossible Cubes - a set of three 3D-printed interlocking 5x5x5 cubes,
from Benno de Grote

Happiness Cubes - designed by Yukiyasu Sekoguchi, made by Alfons Eyckmans from Padauk.
Each cube is 6x6x6 and comprises six pieces.
The pieces are (with few exceptions) based on traditional burr pieces, augmented with additional cubies.
A book called Happiness Cube was published in 2006 (now out of print) showing 35 such designs.
Sekoguchi's website (defunct? Here is a Wayback Machine link Feb 2019 but missing images) showed 160 designs.
Alfons made three for me, including numbers 127, 135, and 151.2.
The burr pieces at the heart of each are:
127 { 58, 104, 926, 975, 1024x2 } - 1 solution 5.4.
135 { 736, 877, 940, 957, 1007, 1016 } - 2 solutions 3.2.
151.2 { 256 (with an extra notch), 704, 943, 960, 992, 1008 } - 61 solutions.
With the cube-filling add-ons to their pieces, the solution for each cube is unique.

Quite some time ago, I got a 3D print of Happiness Cube #20, from Richard Gain.

Tom Jolly has also designed "Cubed Burrs" - such as Cubed Burr II (2004) which I obtained in English Brown Oak.

Designs by Ken Irvine

Turnkey - designed by Ken Irvine Produced under license by the New Pelikan Workshop for Bernhard Schweitzer, made from Mahogany.	Matador - designed by Ken Irvine Produced under license by the New Pelikan Workshop for Bernhard Schweitzer, made from Mahogany.
The Accordion Cube by Ken Irvine, made from Holly, Canarywood, Sapele, Zebrawood, and Walnut, by Eric Fuller. Turns out, in a case of independent discovery, Ken duplicated a 2008 design called "Disjointed Cube" by Mineyuki Uyematsu.
Migraine - designed by Ken Irvine, made by Eric Fuller from Purpleheart
Little Kenny - designed by Ken Irvine Made by Tom Lensch I fiddled with this for a while at NYPP 2016 but could not assemble it, so I knew I'd have to get my own copy. I had Tom send it to me disassembled - I finally succeeded. Only four pieces but a nice challenge.
Little Bruce - designed by Ken Irvine, made by Eric Fuller from Canarywood
The IPP has grown to become a significant logistical undertaking and pulling it off would be impossible without the help of an army of volunteers. Brett and I were fortunate to benefit from the kind efforts of many people who comprised our IPP35 committee. Another IPP tradition is to thank the committee volunteers with a small puzzle gift. Brett and I commissioned Ken Irvine to design a novel interlocking cube, and Brian Menold of Wood Wonders to hand make them. Rob Jones kindly provided funding for the project. We agreed on the name The Ottawa Cube, commemorating the location of IPP35 in Ottawa, Canada, and used Redheart and Maple to give it suitable Canadian colors of red and white.
Pushbutton Burr - designed by Ken Irvine and made by Tom Lensch from Canarywood with Indian Rosewood button pieces. Another great design by Ken. I played with a prototype at RPP in 2017, trying to put the pieces together from scratch. I assembled almost the whole puzzle but could not figure out how to get the last pushbutton piece in! The puzzle is easier if you start by taking it apart, so I recommend having someone do that for you out of sight and handing you the pieces!
Moitié - designed and 3D-printed by Ken Irvine

Designs by Tom Jolly

This is the Cubed Burr II designed by Tom Jolly. I bought this instance, made from English Brown Oak, from Eric Fuller. This is a 6x6x6 cube of six large pieces. The basic plan is that of a traditional six-piece burr, but the pieces have been heavily modified and augmented to form a cube. It requires ten moves to free the first piece. There is only one solution. Tom also designed a simpler version, Cubed Burr.	Rotator - designed by Tom Jolly, made by Eric Fuller from Mahogany, Padauk, and Imbuia Three pieces form a 4x4x4 cube with holes. [Dis]assembly requires rotations.
The Rattle Box, designed by Tom Jolly, made by Eric Fuller from Quilted Ambrosia Maple, Leopardwood, Padauk, Walnut, and Canarywood. A 5x5x5 cube with a hollow interior containing a 2x2x2 cube with one unit missing.
Loopy Cube - designed by Tom Jolly, made by Brian Menold from Osage Orange and Wenge.
Spiral Cube No. 2 - designed by Tom Jolly, made by Brian Menold, from Wenge, Holly, Canarywood, Redheart, and Red Oak.		Tight Noose - designed by Tom Jolly, made by Brian Menold from Wenge and Olivewood
Burr Noose - designed by Tom Jolly made by Brian Menold from Ash, Osage Orange, Iroko, Lacewood, Padauk, Tzalm, and Holly rings	Bundle of Sticks designed by Tom Jolly made by Eric Fuller from Wenge and Holly

Designs by Stewart Coffin

Perhaps Stewart's best-known interlocking polycube design is his Convolution (#30).
This example was made by Thomas Moeller, from Zebrawood and Bloodwood.

Coffin's Three Piece Block - Made by Rob Stegmann!

Stewart Coffin's Three-Piece Block (#38) - one of the few puzzles I made for myself from wood!

This is Stewart's new Involute design, described in his recent book Geometric Puzzle Design. This beautiful instance, in highly polished Padauk with Ebony corners, was made for me by Scott T. Peterson.

Convolution Cousin - designed by Stewart Coffin,
made by and purchased from Nedeljko Woodworks.

Multigrain (275AS) - designed by Stewart Coffin
made by Brian Young
exchanged at IPP35 by Jerry Slocum

Stewart Coffin's Convolution, made by Wayne Daniels	Cube 16, a nice five-piece design by Stewart Coffin, and made from Black Palm, from Bernhard Schweitzer. Purchased at IPP31 in Berlin.
Coffin's 4 Piece Cube made by Brian Menold

Designed and made by Don Closterman Don Closterman lives in Rhode Island and is over 70 years old. He designs and makes a beautiful series of interlocking, sequential (dis)assembly polycube puzzles in cages. Closterman identifies his puzzles using a code of the form T-S-N-P-M, where: T is the type of puzzle � C for cage S is an arbitrary identifier Closterman assigns to a given design with a particular solution method N is simply the number of cubies in the overall puzzle, which seems to include empty spaces (e.g. 6x6x6 = 216) P is the number of pieces including the cage M is the number of moves to remove the first piece, which seems to be omitted if it is only 1 move
A yellowheart 4x4x4 I bought back in about March 2005, code C-2-64-7 which indeed has 7 pieces including the cage, and the first piece comes out directly � I like this one best and have solved it on my own. BurrTools confirms it has two very similar solutions.
A Lyptus 6x6x6 with Walnut plugs at the corners, code C-12-216-19-3.	A Jatoba 5x5x5 Caged Cube (type 4-125-13, from 2-99)
A Canarywood 6x6x6, code C-11-216-13-12. Made in May 07. 13 pieces and requires 12 moves for the 1st piece, including a rotation (!) which stumps BurrTools (although it can discover the single possible assembly, and also the disassembly sequence if I omit the piece that must be rotated). This one I got apart on my own but used BurrTools and the supplied instructions to re-assemble.

Designs by Hidekuni Tamura
This beautiful puzzle called the Twelve Piece Box lies on the boundary between a non-traditional burr and a polycube assembly. The little central cube has a secret, too.	The Six-Block Puzzle looks like a burr, but isn't!	The Ten-Segment Puzzle
The Divide Cube. This one was made by Eric Fuller, from Rosewood.
Kei Cube 1-1c, 1-4c, and 2-4c - designed by Hidekuni Tamura, produced by Puzzlewood Thanks, Chelsea!

Designs by Leonid Mochalov See Leonid's website.
The Russian 13 burr, designed by Leonid Mochalov and made by Mr. Puzzle Australia. Purchased in auction from the John Ergatoudis collection.	8+1 Cube Eight corner pieces and a monolithic central frame (the "plus one"). Each corner piece has an extension with various tabs and notches that inserts through part of the frame and mates with another corner piece - you must find a sequential assembly of the corner pieces. Purchased from Puzzlewood.de.	Burr Cube - by Leonid Mochalov I like this one - when I disassembled it, I didn't think it would take me long to re-assemble it - I was wrong, and I spent several happy hours trying to do it in various incorrect ways. I was surprised that these pieces had so many partial false assemblies. Purchased from Puzzlewood.de.
Mochalov #12 Purchased from Puzzlewood.de at NYPP 2008	Mochalov Cube 2006 Purchased at GPP

Richard Gain has modeled several interesting cube designs you can buy at his Shapeways shop. Richard's philosophy is to make them small and affordable. See Richard's YouTube channel and his blog. You can sometimes find dyed copies for sale at his Etsy shop. My friend Brett has been kind enough to give me several of these as gifts. Thanks, Brett!
Roll Up! Roll Up! designed by Richard Gain Purchased from Richard at IPP31 in Berlin.	Angle-C designed by Richard Gain Purchased from Richard at IPP31 in Berlin.	Elevator designed by Jos Bergmans Purchased from Richard at IPP31 in Berlin.
Bolero, designed by Jeff Namkung, 3D modeled and printed by, and purchased from, Richard Gain	Jive, designed by Jeff Namkung, 3D modeled and printed by, and purchased from, Richard Gain	Quickstep - designed by Jeff Namkung A Level 11.5.3.3 4x4x4 cube. Printed via Shapeways and dyed by Richard Gain
Superstrings designed by Richard Gain Purchased from Richard at IPP31 in Berlin. This won a Jury First Prize at the 2011 Nob Yoshigahara Puzzle Design Competition	Coronation Cube - designed by Richard Gain
Printable Interlocking Puzzle (PIP) #4 - by Richard Gain Check Richard's Etsy shop Microcubology and Richard's Shapeways shop Microcubology. A very nice, difficult, six piece interlocking cube. I got this back in May 2018.
Primary Gain designed by Richard Gain	The World's Smallest Commercially Available Cube Puzzle 7.5 mm side	Inside Out designed by Richard Gain
Cubed Burr II designed by Tom Jolly	Seldom Seen designed by Richard Gain	Happiness Cube #20 designed by Sekoguchi Yukiyasu
Tertiary Gain designed by Richard Gain	The Steady State Cube by Richard Gain.	Switch Cube - Richard Gain
This is Richard's small instance of Tom Jolly's *Twist the Night Away. It is a great design that requires piece rotations to solve. I had fun solving Tom's puzzle at IPP29 in San Fransisco, but I missed out on Eric Fuller's wooden limited edition of them, so it's nice to be able to have an instance of this design, and an inexpensive one at that. It did take a lot* of sanding of the pieces to make this one work, though.		This is *Pivot* by Jos Bergmans Pivot took me a while to solve, and I only managed to do it after I saw an image of the solved cube and deduced the piece placement from the cuts on the faces. It's still difficult to figure out the required sequence of moves and rotations!

Designs by Andrew Crowell Check Andrew's Etsy shop arcWoodPuzzles.
Exolution I, II, III, IV - designed and made by Andrew Crowell
Exolution I - designed and made by Andrew Crowell	Exolution II - designed and made by Andrew Crowell	Exolution III - designed and made by Andrew Crowell
Exolution III - designed and made by Andrew Crowell This design has six pieces and a marble inside, requiring careful orientation.
Exolution IV - designed and made by Andrew Crowell	Locked Cube I - designed and made by Andrew Crowell from Wenge, Yellowheart, and Zebrawood	Split Cube III - designed and made by Andrew Crowell
Though German puzzlist Bernhard Schweitzer lays claim to having coined the term "TIC" to describe the category of "turning interlocking cubes" - and there have been several such cubes created by various designers such as Tom Jolly and Jeff Namkung - Andrew Crowell seems to have achieved the crown of most prolific creator of TIC designs, with over 50 to his credit. I've managed to aquire only a fraction... PedanTIC and FantasTIC, made by Brian Menold: MysTIC and X-TIC - designed by Andrew Crowell, made by Brian Menold PenTIC - designed by Andrew Crowell, made by Eric Fuller I really like this one - I managed to put it together from scratch myself without clues! BioTIC - designed by Andrew Crowell, made by Eric Fuller PackTIC #2 - by Andrew Crowell PackTIC #3 - by Andrew Crowell I was able to assemble this one without hints. You may be tempted to force a piece but it is NOT NECESSARY! A trio of Andrew Crowell's Turning Interlocking Cubes (TICs) made by Brian Menold from various exotic woods: (L to R) PackTIC #5, GalacTIC, and FanaTIC. For me easiest to hardest: FanaTIC, PackTIC #5, and GalacTIC - separating GalacTIC's last two pieces kicked my butt for a while! Pieces: GiganTIC - designed by Andrew Crowell, made by Brian Menold ThreeTIC - designed by Andrew Crowell, made by Brian Menold A 3 piece TIC - 18 moves with 5 rotations TriumviraTIC - another three piece turning interlocking cube (TIC) designed by Andrew Crowell, made by Brian Menold I love how Andrew can create a challenge using only three pieces! It is very easy to visualize where the pieces must go in the completed puzzle, but maneuvering them into position is non-trivial! I did manage to assemble TriumviraTIC from scratch, but ThreeTIC still has me stumped. TripleTIC, NeuroTIC, and TriadTIC - designed by, made by, and purchased from Andrew Crowell. A trio of Andrew's three-piece turning interlocking cube (TIC) puzzles. (I also have TriumviraTIC and ThreeTIC in wood made by Brian Menold.) Of these three 3D printed puzzles, NeuroTIC is my favorite. You can reason backwards about the necessary maneuvers. Shipped unsolved. Rotothorpe - by Andrew Crowell Thanks! ElfTIC - by Andrew Crowell 3D printed for me by Brett - Thanks!

Modular Polycube Construction Elements
One of the coolest things is LiveCube - you can build your own polycube puzzles! See U.S. Patent 6679780 - Sywan-Min Shih 2004.	I was contacted by Carlo Gitt who informed me that this small brown 4x4x4 cube was made by him for IPP11 and is called the CARLOG.CUBE - the six pieces model the letters of his first name, and his surname initial. The blocks are called CENTICUBES, and he also used them for his IPP35 Ottawa exchange puzzle the OTTAWA-IPP35-CUBE. Thanks for the info, Carlo!
The Never Ever Cube is also made from unit modules. In this case the modules are cubic frames, and there are rubber inserts designed to fit into the faces and bind to another face on an adjacent unit cube. Personally I think the LiveCube design is better, as there are fewer pieces to worry about, and the connections are more firm.	D Box - a puzzle construction kit, designed by the Light brothers See www.dboxpuzzle.com
Interlock, from Popular Playthings
Fight Cube, in the Playable Metal series. A set of aluminum bricks that can be screwed together to form puzzle piece shapes. Designed and manufactured by Taken Fun & Art Co. Ltd. of Taiwan [website]. See a video here. I purchased a 3x3x3 kit, and then a 4x4x4 kit. The 4x4x4 kit simply includes two 3x3x3 kits, and a package of extra pieces (with screws) to round out to 64 units. There are no plans for any 4x4x4 cubes, so you have to figure out how to make your own. Note that since there will be only so many "plus" and "minus" pieces, you will have to figure out how to allocate them among the puzzle pieces you wish to create.

Diagonally Joined Polycubes

This small group contains polycube puzzles where the pieces contain cubies joined diagonally, via some sort of "spars" - these spars can be metal, nylon, or 3D printed. The cubies must be beveled so that the spars can travel through the interstices between cubies.

The Edge Corner Cube II by Markus Goetz. Winner of an Honorable Mention in the 2005 IPP Design Competition.

For the longest time, my example sat in an unsolved state. During a recent inventory, I picked it up again and solved it. I took photos along the way and show them here for your edification. There are seven pieces, two of which are identical, and one of which is a unit cubie. This distinguishes the Edge Corner Cube II from the Liberal Cube, which has no unit cubie piece.

Edge Corner Cube II

Liberal Cube
designed by Markku Vesala,
purchased from and made by Eric Fuller
from Purpleheart and Nylon.

Non-Void Cube - designed by Andreas Röver
Four pieces.
No internal voids, yet still manages to achieve level 4.3.3!
Purchased at IPP37 in Paris.

Edge Corner Cube Variation (green) and Non-Void Cube Variation (blue) -
both designed by Christoph Lohe,
3D printed by and purchased from Andrew Crowell
See Andrew's Etsy shop arcWood Puzzles.

Quoting Lohe from Andrew's page:

ECC Var - I was always fascinated by Markus Goetz' Edge-Corner Cube.
It looks like a simple 3x3x3 cube but the pieces connect cubies
not only side by side, but also through some edge and corner connections.
My take on Markus' idea has a slightly higher level 1.13
for the removal of the second piece than Markus' original (level 1.9).

NVC Var - Markus Goetz' ECC had motivated Andreas Roever to [create] his Non-Void Cube.
It requires more than one move for the first piece. How is a level higher than 1 possible,
if the 3x3x3 volume is completely filled? The magic is in the cubies' bevels!
The bevels create channels which are partly empty, so it is not just a simple 3x3x3 puzzle.
My take on Andreas' idea has a slightly higher level 5.2.6.1.2 than Andreas' original.

Happy Cubes/Snafooz (Foam Assemblies)

At the Jan. 2005 NYPP, I got these from Norman Sandfield, not knowing what they were. There were originally 4 blue and 4 yellow cubes, but I gave away 2 of each to various folks who wanted them. All the blues and yellows are each made of the same set of six different pieces. Since receiving a copy of the CFF newsletter issue 50 (Oct. 1999, Part 4/6), I have determined that they are all equivalent to the "Tokyo" version of the Wirrel Warrel, also known as "Happy Cubes."	Inexpensive puzzle pieces can be cut from dense foam mats. Several varieties of puzzles in the "Wirrel Warrel"/"Happy Cubes"/Snafooz family have been implemented using this material. Happy Cubes were invented by Dirk Laureyssens - read more at the Cricro site. Cricro provides a pair of pentagonal faces. Happy Cubes are being marketed by Happy n.v.	Inspired by reading about Happy Cubes in the CFF newsletter and following information on Jurgen Koeller's Happy Cubes page, I made my own set of generic pieces from LiveCube. I used 8 cubes each for the 6 centers (in black) and an additional total of 44 yellow cubes to be distributed about the edges, as required by the various piece configurations.
Snafooz makes 6-piece cube puzzles where the pieces are cut from foam slabs. They are similar to Happy Cubes, but the Happy Cubes are based on a 5x5 square face, while the Snafooz are based on a 6x6 square. Snafooz are often issued as corporate promotional give-aways, and I have accumulated several from various trade shows. I also have a promotional puzzle based on a 7x7 square.	This is "Mystery Shapes" designed by Oscar van Deventer, issued in 1993 by Binary Arts. Four cubical puzzles made of six foam pieces each, but with extra confusing ridges running around the faces.	The "Eraser Cube" is made from eraser-type rubber material, and is based on a 4x4 square side.
Puzzle Erasers Set Paladone Products Ltd.
Take Me Apart - designed by Bruce Viney, made by Brian Menold at Wood Wonders, from Padauk and Cherry A side-5 cube with a smaller nesting side-4 cube inside.

Cube-and-Plank

Triple Trouble Purchased from Potty Puzzles.	Black and White by Kubi Games Purchased from GPP.	Double Trouble Purchased from Pentangle. I really like this one - six different pieces loosely interlock. Each consists of a plank and two or more half-cubes attached in various orientations. They can be assembled using logical deduction.
Red Planks designed by Jos Bergmans. Nine pieces, made by Brian Menold from Redheart and Maple.
Blue Planks - designed by Jos Bergmans, made by Brian Menold from Padauk and Osage Orange

Polyhedral Assemblies

I am the proud owner of Corner Cube #28 by Lee Krasnow.

It has six dissimilar pieces which assemble only one way. It is not easy to find the sliding axis to disassemble the puzzle! My instance is made from beautifully figured Tulipwood, Brazilian Kingwood, Cocobolo, and Bocote. I bought this directly from Lee in 2003.

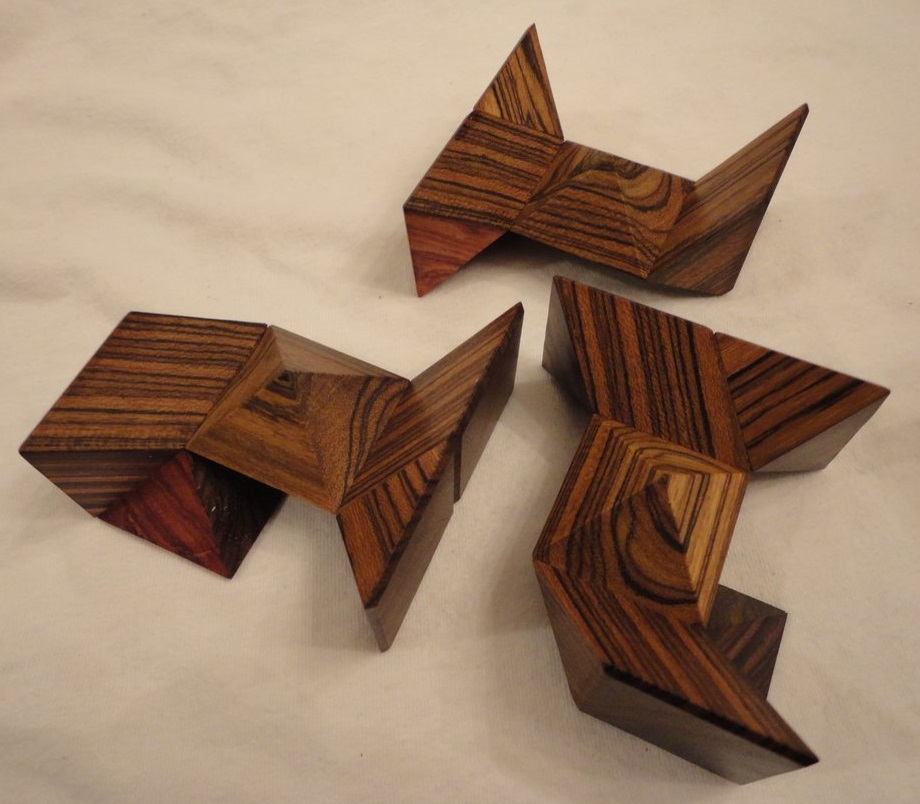
Corner Cube No. 28 - Lee Krasnow

One of my favorites is this "Ribbon Keyvos" made for me by Michael Toulouzas of Greece:

My Keyvos is made of Bois de Rose, Wenge, and Mahogany	It's not easy to find the right slide...
There are six distinct pieces	It comes with a certificate

This is a "Star Version" of the Brain Attack designed and made by Michael Toulouzas. I purchased this in a Baxter auction.

These photos show the assembled puzzle from various angles. The shape is a rhombic dodecahedron.

Here is the puzzle coming apart...

Here are the six pieces. The core of the puzzle fits together in much the same way as Stewart Coffin's designs.

Brain Attack - Michael Toulouzas

Here are some nice puzzles from Brian Menold.

Four Piece Pyramid - Stewart Coffin - Menold - Holly
The Four Piece Pyramid designed by Stewart Coffin, made by Brian from Holly. The units are rhombic dodecahedra.

Octahedral Cluster - Coffin - Menold
The Octahedral Cluster designed by Stewart Coffin, made by Brian from Walnut. The units are rhombic dodecahdra.

Four Piece Pyramid - Stewart Coffin - Menold
Four Piece Pyramid designed by Stewart Coffin
beautifully made by Brian Menold
from Redheart, Padauk, and Yellowheart
A very tricky assembly of four pieces!

Wayne Daniel Interlocking Puzzles

These are from Interlocking Puzzles. Some were designed and/or made by Wayne Daniel. All of these puzzles are very well made and attractive.

4 pc tetrahedron - Interlocking Puzzles
4-piece Tetrahedron 5 pc tetrahedron - Interlocking Puzzles
5-piece Tetrahedron
Padauk and Beech
Six Piece Tetrahedron - Daniel

Six Piece Tetrahedron - designed and made by Wayne Daniel
I had been after this one for a while, to round out my set of tetrahedrons by Wayne Daniel -
and it does not disappoint! Beautifully made and quite a challenge. I love it!
Just look at those intricate pieces! How did Wayne manage this??
IP - dual tetrahedron
Dual Tetrahedron IP - truncated cube
5-piece Truncated Cube
The Truncated Cube is surprisingly hefty, and very nicely finished. Very unusual piece shapes.
Brazilian Cherry (Jatoba)

6-piece Truncated Cube
Padauk
7-piece Truncated Cube
Jarrah
For me this has been the most difficult of the three truncated cubes.
Golden Rhombic Icosahedron - Interlocking Puzzles
Golden Rhombic Icosahedron IP - truncated octahedron
Sequential Truncated Octahedron
Maple
Golden Rhombic Icosahedron - Tigerwood
Golden Rhombic Icosahedron - Chechin
I found a Tigerwood version of Wayne Daniel's Golden Rhombic Icosahedron.
I already had another version I believe to be the IPP17 exchange gift from Abel Garcia, made from Chechin wood. They have different pieces.
John Rausch describes the full set on his PuzzleWorld website.
Each puzzle has only four pieces, but they are difficult to take apart and to assemble.
The Zebrawood version has a slightly rounded interior edge to permit [dis]assembly.

Twelve Bowties 2 - Daniel
Twelve Bowties 2 - designed and made by Wayne Daniel
exchanged at IPP35 by Marti Reis
Pulsar Pulsar Pulsar
Pulsar Pulsar
This puzzle is called Pulsar. It is based on a design by Victor Genel, modified by Benji and Ginda Fisher, and served as the Fishers' exchange puzzle at IPP 20.
It was made by Wayne Daniel. In the modified design, two pieces are fused to two others, and the cubic central cavity is occupied by a bisected cube.

Designs by Stewart Coffin

The Puzzling World of Polyhedral Selections - Stewart Coffin

Geometric Puzzle Design - Stewart Coffin

It is difficult to overstate the contributions of Stewart Coffin to mechanical puzzle design. In fact, it is difficult to decide where in this website to put a subsection devoted to him, since his ideas have become so widely applied across the field. Many of his primary contributions do lie in this area of interlocking polyhedral assemblies. Stewart coined the term "Ap-Art" to describe his "sculptures that come apart." In the 1970's through 1990's Stewart ran a puzzle club of which many of us including me can only wish we had been members.

With the publication of his The Puzzling World of Polyhedral Dissections (hosted on John Rausch's PuzzleWorld site), Stewart literally "wrote the book" on entire classes of interlocking puzzles that simply did not exist before he thought of them. Moreover, Stewart has been incredibly generous in allowing puzzle enthusiasts worldwide to utilize his designs without financial impediment. For these and other reasons, in 2006 Stewart became the first recipient of the IPP Nob Yoshigahara Award for "Lifetime Achievements in Design, Craftsmanship, and Popularizing Mechanical Puzzles."

Stewart has a new book out in 2007, Geometric Puzzle Design. Several other related books are described, offered, and/or hosted online at John Rausch's PuzzleWorld site.

I've managed to acquire a few puzzles designed by Stewart Coffin. Some are originals bearing his mark "STC" while the rest are copies of his designs made by other skilled woodworkers.

Based on the compendium called Ap-Art, written by Stewart and produced by John Rausch, I put together the diagram below which is my attempt at showing a "family tree" of Stewart's interlocking puzzle designs.

Stewart Coffin Interlocking Puzzles Family Tree

Jupiter by Stewart Coffin - Vigouroux
This is Jupiter - designed by Stewart Coffin, and perhaps his most iconic work. See U.S. Design Patent 232571 Coffin 1974
This instance was made by French craftsman Maurice Vigouroux
This Jupiter came in 60 unit pieces, 10 each of six colors. Five unit pieces assemble to make a "star" and 12 such stars go together, in two halves of six stars apiece, to form the puzzle.
The colors must be distributed such that colored pieces mate, and all pieces of a given color run parallel.
Triangular Prism - STC - Daniel
Triangular Prism (#12) - designed by Stewart T. Coffin
made by Wayne Daniel

Double Triangular Prism

This is a Double Triangular Prism, based on the Triangular Prism #12. This instance was made by Pelikan - I obtained it from Bernhard Schweitzer. Shown assembled, beginning disassembly, in two halves, and in six dissimilar, asymmetric pieces.

Sphinx Transformed - McCallum
Mark McCallum made this beautiful Sphinx Transformed for me. Thanks again, Mark! It's a rhombic triacontahedron, a relative of Stewart Coffin's Design No. 72. The woods include: Kingwood, Spotted Ebony, Bird's Eye Maple, Ziricote, Ceylon Satinwood, Chakte Viga, Narra, Tulipwood, Redheart, Macassar Ebony, Ebony, and Bocote.
Ring of Diamonds - McCallum
Mark also made the Ring of Diamonds (STC #13-B) in walnut. The precision is masterful! Thanks, Mark!

12-Point - Stewart Coffin
Twelve Point (33) or Augmented Second Stellation
made by Stewart Coffin
Pennyhedron - Stewart Coffin
Perhaps one of Stewart's best-known designs is the simple two-piece Pennyhedron (52). I purchased this one made of Wenge from Stewart at IPP26. Fancy This (115-A) - IP
Fancy This! (115-A)
made by Interlocking Puzzles
Russian Balls - Coffin - Krasnow
Russian Balls (6-color set) - a Matryoshka nesting of Stewart Coffin's Pennyhedron,
made by and purchased from Lee Krasnow.
Ball Octahedron
designed by Stewart Coffin and made by Wayne Daniel
exchanged by Jerry Slocum at IPP32.
Jerry's actual exchange puzzle was It's Nuts, a copy of the Screwy Screw by Scott Elliott. Since I already have a copy, Jerry was kind enough to substitute his puzzle from IPP29.
Prism Cell #192 - Stewart Coffin
Prism Cell (192)
STC 2003
purchased from Stewart at IPP26 Polly-Hedral - Stewart Coffin
Polly-Hedral was made by Stewart in 2006 and was Jerry Slocum's exchange puzzle at IPP26.
12-piece Separation - Thomas Moeller Coffin's Separation - Moeller
12-piece Separation (85)
Two copies made by Thomas Moeller

Fellow puzzler John Rausch attends RPP and has several times
very generously held a round-robin puzzle give-away.
I scored one of Lee Krasnow's 3D printed examples of
Stewart Coffin's Twelve-Piece Separation puzzle.
Thanks, John!
12 Piece Separation - Coffin - Krasnow

Stellation Set - Krasnow
Stellation Set - by Lee Krasnow, purchased at PuzzleMaster.ca

Star of David - Improved (37A)
six pieces
unknown craftsman Four Corners - Thomas Moeller
Four Corners (6)
made by Thomas Moeller
See U.S. Patent 3885794 - Coffin 1975. Triumph - Thomas Moeller
Triumph (15)
made by Thomas Moeller
Fusion Confusion - Interlocking Puzzles
Fusion Confusion (15-A)
made by Interlocking Puzzles.
Augmented Stellation - designed by Stewart Coffin (#46 - Vega), made by Brian Menold from Plum and English Sycamore woods. A simple puzzle having six identical pieces, but very nice work - edges straight and sharp! The Vega is a derivative of the classic diagonal burr - its lineage is: diagonal burr -> diagonal star Sirius #4 aka first stellation of the rhombic dodecahedron -> Nova #8 aka 2nd stellation of the RD -> Vega.

I purchased this "Multisphere" by Janod from Puzzlemaster.ca. It is Stewart's Scorpius (5). Dislocated Scorpius - Pelikan
Dislocated Scorpius (16)
Purchased from Bernhard Schweitzer Broken Sticks - Pelikan
Broken Sticks (32)
Purchased from Bernhard Schweitzer

Provenance unknown, but I call this a
Pointed Scorpius - six identical pieces - each in turn made from 4 sticks

Nova (8)
six identical pieces
unknown craftsman
Vega (46)
six identical pieces
unknown craftsman
Square Prism
six identical pieces
unknown craftsman

Scott T. Peterson made this Super Nova (14) in Bird's Eye Maple and African Blackwood.
The Hill
Introduced at IPP26 in 2006 at Boston. Unusual Coffin design, as a single piece comes out on the first move, then another piece, with the remaining four requiring coordinate motion!
Split Star - Mark McCallum
This is Stewart's Split Star (75), made by Mark McCallum. It is a two-tier design, with a garnet at its heart and outer pieces of bubinga wood forming the diagonal star shape.

I bought this beautiful version of Stewart Coffin's Garnet (60) design, from Cubicdissection. It was made by Mark McCallum. Stewart calls it the dissected rhombic dodecahedron, and it is described in chapter 15 of Stewart's book. There are nine possible distinct asymmetric pieces, and this version is made from pieces A through F. Disassembly is fairly easy, but if you mix up the pieces, reassembly is challenging. My approach is to try all possible groups of three to make a half. The remaining three must form a mating half. A group of three pieces might fit together in several ways, so one must explore the possibilities carefully.

Garnet - Mark McCallum

Starting in the top row, from left to right, the piece IDs and woods are:
(A) Macassar Ebony, (B) Bocote, (C) Honduras Rosewood, (D) Holly, (E) Bloodwood, (F) Brazilian Rosewood.

Garnet Ball - Pelikan
Pelikan's Garnet Ball - a spherical version of Stewart's Garnet. This puzzle uses mirror images of pieces A thru F.
Purchased from Bernhard Schweitzer
Here is a beautiful version of Stewart Coffin's Augmented Four Corners puzzle (34), made from Canarywood and Redheart by Mark McCallum, and purchased from Cubicdissection:
Augmented Four Corners - Mark McCallum

Rosebud Rosebud (easy assembly) Rosebud pieces
Scott T. Peterson has made a Rosebud (39) for me, from Bloodwood and Lignum Vitae, a very aromatic wood. There are six pieces - three "left-handed" and three "right-handed." They are extremely difficult to assemble into the Rosebud configuration. There is, however, a much easier assembly, shown in the center above.
Rosebud - Coffin - Bell
Rosebud - designed by Stewart Coffin, 3D printed by George Bell at PolyPuzzles
The individual pieces can be dis- and re-assembled, making overall assembly much easier if desired.

Combination Lock - Coffin - Nedeljko

Combination Lock - STC #128 - designed by Stewart Coffin,
made by Nedeljko Woodworks

Pieces of Eight
Pieces of Eight (77)
made by Interlocking Puzzles. (Some nice photos from the old IP website.)

Coffin's Diagonal Cube - Bell
Stewart Coffin's Diagonal Cube design -
modeled by George Bell using BurrTools and printed by Shapeways -
available at George's Shapeways Shop.
Diagonal Cube - Coffin - Crowell
Diagonal Cube - designed by Stewart Coffin, made by Andrew Crowell
Check out Andrew's Etsy Shop arcWoodPuzzles

I received a beautiful Stellated Improved Square Face puzzle (SISF for short),
designed and made by the talented Scott T. Peterson [W] [Y],
based on the Square Face Puzzle (74A) designed by Stewart Coffin.
My copy is made from Blackwood and Lacewood.

Cluster Buster STC #47 - Solitude Summit Woodworks
Two beautiful wooden puzzles made by Solitude Summit Woodworks on Etsy,
both designed by Stewart Coffin: All Star #95, and Cluster Buster #47
Both are substantial and playable, and made of beautiful hardwoods, though fit is loose.
Design X-3 - Coffin - SSWW
Design X-3 - designed by Stewart Coffin,
Produced by SolitudeSummitWoodWorks
in Canary and Cocobolo woods.
The Park (#207) - Coffin - SSWW
The Park (#207) - designed by Stewart Coffin,
Produced by SolitudeSummitWoodWorks
in Shedua wood.

Mark McCallum Octo-Burr
This is Stewart Coffin's Octo-Burr design, made by Mark McCallum and purchased from CubicDissection. See the pieces on John Rausch's site. Burr Circus - Coffin - Fuller
Burr Circus, designed by Stewart Coffin (STC #116) and made by Eric Fuller, from Purpleheart. Six sticks, having notches both slanted and tilted. Not easy to make, nor easy to assemble. Stewart Coffin Lock Nut
Stewart Coffin's Lock Nut

[47]

The 3M Hectix and The Geo-Logic Line

Stewart Coffin licensed several of his polyhedral designs to various companies which produced them in plastic.

Hectix - rwb Hectix - white Hectix clear
Stewart Coffin and Bill Cutler both independently came up with the design of 12 interlocking notched hexagonal sticks (copied by Tenyo's "Papa" puzzle shown elsewhere).
Stewart's version was produced commercially by 3M, who called it "Hectix."
I've obtained the red/white/blue, white, and clear versions of Hectix.
See U.S. Patent 3721448 - Coffin 1973.
The Hectix design has been widely copied - here is a wooden version produced in Japan as part of the "Woody" line of puzzles:

Woody Craft Hexsticks

Joy of Hex - Two Brass Monkeys
Joy of Hex - by Two Brass Monkeys
in collaboration with Derek Bosch
This great product extends the original idea of a burr comprising 12 interlocking notched hexagonal sticks into a family...
Borrowing heavily from their website description:
They've done an analysis of all solid, twelve-piece burrs, with no solid key piece, and selected and released three designs: MISSIONARY (easiest); BISH, BASH, BOSCH - requiring coordinate motion; and GROUP HEX - incorporates the maximum number of different piece types (8 of 9 possible types of notched hexagonal piece) that has a single unique solution.
Included with the three sets are: Five bonus milled brass hex pieces, a "Joy of Hex" manual of 30 hexual positions and solutions written by consultant hexologist Dr Eric Shun, and a hex aid (jig/stand) to help with the most challenging positions. These items turn the three puzzles into a burr set, with 30 published challenges and over 97,000 other possible assemblies.
Each hex piece is milled from solid brass and is 6cm / 2.36 inches long. An assembled puzzle weighs about 1.8lbs or 840g. I got the complete set. The entire set weighs in at 8.5lbs.
I have accomplished the Missionary position:
Joy of Hex - Two Brass Monkeys
When I received my example of "Group Hex" it mistakenly included an extra BC rod instead of the required ABC rod. Brass Monkey Steve very kindly and promptly sent me the missing part, and then named an assembly that would utilize the extra BC rod after me - I am honored, probably...
Joy of Hex - Position 31 - Stegmann Screw Up

Geo-Logic boxes Penta-Logics box Penta-Logics Galaxy I w/ pcs
Some of Stewart's other designs were produced commercially in plastic as part of the Skor-Mor "Geo-Logic" and "Penta-Logics" lines. I obtained Tauri, Cetus, Aries, and Uni in 2-in-1 packs, and a Nova separately. The Penta-Logics included Spirus and another Nova. Luckily, all of the pieces are intact. Each puzzle is composed of a set of six particular identically-shaped pieces (a different piece type for each puzzle), which fit together either in two halves or using coordinate motion.
The Tauri is described in Stewart Coffin's book The Puzzling World of Polyhedral Dissections (see fig. 97).
The Penta-Logics set allows you to make a "Galaxy 1" (shown, with leftover pieces) and a "Galaxy 2" (not shown).
Geo-Logic Aries
Aries Geo-Logic Cetus
Cetus Geo-Logic Nova
Nova Geo-Logic Tauri
Tauri Geo-Logic Spirus
Spirus Geo-Logic Uni
Uni (A real pain to assemble!)
Cetus pieces
Cetus instructions and six identically shaped pieces.
Tetrahexed - Coffin
Tetrahexed - designed by Stewart Coffin,
made by Wayne Daniel, exchanged at IPP35 by Stan Isaacs
A nice wooden version of Coffin's 1971 Cetus issued by Skor-Mor
Geo-Logic Nova
Nova Geo-Logic Spirus
Spirus

Geologic Aries - designed by Stewart Coffin,
issued 1972 by Nylon Products Corp. MA
pink cube pieces
The Geo-Logic line also included an "exploding cube" called "Inner Peace." It has six identical pieces.
I obtained one but with no box - I did not know what it was until I found a box shot on the web.
The six pieces can be built into a cube or a stellated rhombic dodecahedron. The latter is a very tight fit.

Pinned Assemblies

This is a puzzle called "Rube's Cubic" purchased from IQ Puzzles. It is also described in Coffin's book, as the Pin-hole Puzzle. As Stewart says, it is fairly easy to assemble.	This is Coffin's Corner Block puzzle, made by Kerry Verne from Yellowheart, Bloodwood, and Walnut (pins). Purchased from CubicDissection. Stewart describes this type of puzzle in his book, showing a set of possible pieces. Coffin's Corner Block uses pieces numbers 1, 2, 3, 7, 8, and 12, and one pin. Stewart says he has been unable to find a selection of pieces that can be assembled one way only. This set has two solutions.	This is the "Ancient Key" puzzle, from the Mandalay Box Company. This is a variant of the Corner Block. The Ancient Key uses pieces numbers 1, 2, 3, 7, 11, and 12, and one pin.
Logical Progression Interlocking Cube - designed by Rick Eason, made by Rick, and Eric Fuller from Walnut and Oak. Lots of holes and dowels. A single sequential-assembly solution. The puzzle is supposedly solvable by analysis rather than guesswork. Rick describes the puzzle at his website and gives a link to a page with detailed logical analysis.

Arjeu CT442 (Colorado) purchased from Ishi Also known as Electrons, by Janod.	Arjeu CT210 purchased from Ishi	Arjeu CT795 (Cactus) gift from Jeff Taylor
This is Arjeu's Quadro (CT755), purchased from Ishi. It is a simple version of Coffin's Locked Nest puzzle and is described in Coffin's book in Chapter 13 (see figure 130b).	Tetralott by Markus Goetz (Philos)	Arjeu CT5152 aka Achille
Tipi - Bits and Pieces	Woodn't Cross by Mag-Nif 1974	Charles O. Perry's The Double (my favorite).
Alchemy, designed by Brian Young, made by Eric Fuller, from Ash wood.	The Aqube, purchased from Puzzlemaster. (I got the Psychodelic version - blue pieces shown for example.)	Spotted Cube, designed, made, and exchanged by Ken Ewers at IPP32
Rosemary Howbrigg sent me one of her IPP33 exchange puzzles, Spare Parts, designed and made by Stewart Coffin. Thanks so much, Rosemary!

Irregular Assemblies

This is my catch-all group for interlocking puzzles made of pieces and/or forming shapes that aren't geometrically easily described. Some are figural representations of various animals or objects, while many are abstract geometric fantasies. Sometimes the pieces of the puzzle are similar, sometimes dissimilar. They can be made from wood, or plastic, or metal.

Vinco Puzzles

Vaclav Obsivac (aka "Vinco"), makes wonderful wooden puzzles. I have acquired several, some purchased from puzzlemaster.ca, others from Cleverwood or directly from Vaclav.

Cross in Ball
Prismastar
Twister 1
UFO
UFO Cleverwood - Hedgehog
The Hedgehog
purchased from Cleverwood Obsivac - Trick Box
The Trick Box is also a coordinate motion puzzle - darned hard to assemble.
Obsivac - IPP26 gift
This small 4-piece "Cube Vinco" was a gift from Vaclav at IPP26. Obsivac - Cubetresor
Cubetresor
This is the Button Prison from B & P.
Two-U Two-U
This is Two U. See Vinco's website for a nice chart of various types of "half-cube" puzzles. This puzzle reminds me of Coffin's Pieces of Eight. Purchased from Vaclav at IPP28 in Prague.
This is Vinco's Vidly Half-Cubes. Although technically this isn't an Interlocking puzzle, I show it here since it is another of Vinco's series of half-cube designs. A gift from Vaclav at IPP28 in Prague. Thanks! Xcruci8 Xcruci8
Xcruci8 - designed and made by Vaclav Obsivac
Exchanged at IPP28 by Laurie Brokenshire
Purchased from Laurie at NYPP2011

IPP 31 - octahedron - Vinco

Try-Cycle designed and made by Vaclav Obsivac, exchanged by Laurie Brokenshire

Helical and Tensegrity

Helical puzzles use a twisting motion. Tensegrity puzzles interlock under tension and compression and can often be more of a dexterity challenge.

This is George Hart's "Screw Cube" - a two-piece interlocking puzzle George invented and 3D printed with white nylon. I got prototype number 1 from him at one of Brett's Manhattan puzzle dinners.
George Hart Screw Cube
It's not too difficult, but everyone who plays with it likes it and is a little stumped at first. I think it's a classic. Thanks again, George!

Join the Club - Scott Elliott Diamond Engagement - Elliott
Diamond Engagement - designed,
3D printed, and exchanged at IPP35 by Scott Elliott Halve a Heart - Elliott
Halve a Heart - designed and made by Scott Elliott S'Paid in Full - Elliott
S'Paid in Full - designed and made by Scott Elliott

Puckup - Elliott
Puckup - designed by Scott Elliott Peppermint - Elliott
Peppermint - designed by Scott Elliott Twisty Trillion - Elliott
Twisty Trillion - designed by Scott Elliott

Tubular Burr - Bosch
The Tubular Burr by Derek Bosch.
Purchased from Derek at IPP 29 (2009) in SF. Derek went on to elaborate his ideas on helical structures in burrs...
Helical Burr - Bosch
Helical Burr - Derek Bosch - dyed Shapeways 3D print
Derek's clever Helical Burr won the Jury Grand Prize
in the 2013 Nob Yoshigahara Puzzle Design Competition.
Four pieces - two assemblies - one is level 11.

HELLical Burr designed by Derek Bosch
as a more fiendish follow-up to his 2013 prize-winning Helical Burr.
Four pieces. Printed by and purchased from Steve Nicholls.
Kevin Sadler posted a YouTube video of the disassembly here. Twiddle Dee and Twiddle Dum - Bosch - Nicholls
Twiddle Dee and Twiddle Dum
A new pair in a continuing series of fiendish helical burrs
designed by Derek Bosch
3D printed for me by Steve Nicholls
I asked Steve to make them "opposite" each other.
(Also, Dee has two slots in the end, Dum only one.)
Dee is rated the more difficult of the pair, with 10 more moves and many extra dead ends.
W(h)orl(e)d Burr - Derek Bosch
W(h)orl(e)d Burr designed by Derek Bosch
3D printed by Steve Nicholls Oliver - Bosch
Oliver - Derek Bosch's latest helical burr puzzle, printed by Steve Nicholls.
Polar Burr - Bosch
Polar Burr - another helical burr designed by Derek Bosch. Sweeney Todd - Bosch
Sweeney Todd - a 4-piece helical burr by Derek Bosch
43 moves to remove the first piece.
Printed in PLA by The Two Brass Monkeys.

Plato's Secret variation
Plato's Secret
See U.S. Patent 3695617 - Mogilner and Johnson 1972. See also D0224974 - Mogilner 1972.
A puzzle based on tensegrity - "tensional integrity" - a balance between tension and compression. (For another example, see Bathsheba Grossman's "Moon Pi.")
A number of sticks with slots at each end, a cord, and a ball for the center. The first challenge is to remove the orb without disconnecting anything. The second challenge is to (re)build the structure - lash the sticks together in the proper pattern to create a polyhedron around the ball. The patent describes a structure with 12 sticks, and mentions 9 and 15-stick versions, claiming that tensegrity structures can be made from any number of sticks. The puzzle has appeared with 10 sticks, forming a dodecahedron (12 pentagonal faces, 20 vertices).
I've also seen this called the "Philosopher's Knot" (1975 by whom?), "Plato's Plight" (Mag-Nif 1971), "Cobweb" (Reiss), "Knit Wit" (Romany 1974), and "Merlin's Stone" (Skor-mor). Supposedly it has also been called the "Philosopher's Stone" though I have not seen that version.
Richard Whiting has a solution to a version he calls Whiting's Woe on his website.

Chain Reaction - Invermark 1987
Chain Reaction - a vintage interlocking puzzle/toy, invented by David Brown.
Invenmark Ltd. 1987
I found the relevant patent WO1988008320 A1 by searching for Invenmark 1987.
For some reason Google Patents does not show the diagrams, but Espacenet does.
(Although that link may get you into a weird "prove you're a human" loop...)
Kind of a tensegrity/dexterity hybrid. I use the term "tensegrity" but it's not really correct to apply to this construction -
I'm getting at the "push-pull" going on - the patent describes it like this:
"A first pair of limbs of the first frame holds captive therebetween a second pair of limbs of the second frame;
a first pair of limbs of the second frame holds captive therebetween the second pair of limbs of the third frame;
and a first pair of limbs of the third frame hold captive therebetween the second pair of limbs of the first frame."

Moon Pi Moon Pi
This is a sculpture puzzle called "Moon Pi" made by the artist Bathsheba Grossman, using a direct-metal 3-D printing process driven by a CAD design. I learned about it via James Dalgety's Hordern-Dalgety Puzzle Museum site.

The Peppermint Twist puzzle was introduced at IPP17 by John Ergatoudis. It consists of five twisted metal rods that, surprisingly, interlock. If one rod is slid out of the bundle, it collapses, and is a challenge to reconstruct.
George Hart - 12 stick puzzle
A 12 Sticks puzzle by George Hart, 3-D printed on his Makerbot. This is the 1st of his series of stick puzzles!
Nova Plexus - Wyvill - TwoBrassMonkeys
Nova Plexus - designed by Geoff Wyvill, made by and purchased from TwoBrassMonkeys
I had been after a Nova Plexus puzzle ever since reading about it in Slocum's 1994 The Book of Ingenious and Diabolical Puzzles -
but they were only produced in very limited quantity and had been impossible to find until now.
Check Steve and Ali's Etsy shop TwoBrassMonkeys to snag one of the remaining limited edition versions.
Wyvill's site has a page giving the history of the Nova Plexus puzzle.

Misc. Interlocking

Additional interesting interlocking designs...

O.S.M. Ball
This beautiful spherical puzzle is called the O. S. M. Ball,
designed by Jakub Dvorak of the Czech Republic.
I purchased this from Bernhard Schweitzer at IPP28 in Prague.
Eight pieces. The first and second moves are tricky to discover. Made from beautiful hardwoods. Muto Cube (Japan)
This is a Muto Cube from Japan. I've seen it on only one other collector's ( Martin Watson's ) site.

Oskar's Matchboxes (Fuller)
These are Oskar's Matchboxes.
The first set I got from gemanigames.com. They're not really matchboxes - the "interior" pieces are solid, not hollow boxes. Also, not all interiors fit easily into all containers and the ends have obvious saw marks with overall finish being mediocre. Still, I am happy to have them and the puzzle is fairly challenging. The solution configuration does fit together nicely. I have wanted this puzzle since first reading about it on page 81 of Slocum and Boterman's Puzzles Old and New way back when, and I was glad to find a vendor selling it.
Eric Fuller made the second set, from Madrone and Aformosa woods. These are beautiful - the boxes actually have walls and interiors and the fit is great.

Matchbox Play Six designed by Olexandre Kapkan
made by Eric Fuller
Eric has this to say about this puzzle: "Oskar's Matchboxes is one of my favorite puzzles, and as soon as I saw that Olexandre had expanded on that concept I was eager to make the Matchbox Play Six. With three sets of mirrored pieces, there are several symmetrical solutions and even a couple non- symmetrical solutions. This puzzle is a lot of fun to play with and is a bit easier to solve than the five piece version by Deventer. It displays beautifully and is one you can hand to a trusted guest to experience the feel of a high end puzzle without the frustration of an extraordinarily high level burr. The construction of this puzzle is robust and detailed. Detailed and intricate shoulder joinery on the drawers and sheaths makes it much stronger than the .125" thick wood would indicate. Each puzzle was individually sanded to fit, and the feel is excellent overall."
Oskar's Cubes - Tom Lensch Oskar's Cubes (metal) - Bits and Pieces
These are Oskar's Cubes.
The large wooden version is from Tom Lensch.
The small aluminum version is from B and P.
You can see the pieces at Ishino's site.
The Devil's Half Dove-n and the Devil's Other Half Dove-n.
Designed by Pavel Curtis.
From Puzzlecraft, gifts from LuAnn.
Planks - Pavel Curtis
This puzzle is called Six Tabbed Planks.
It is made from acrylic. I really like it - the proper configuration can be logically deduced with a little effort, and the assembly is sequential.
Unknown designer. Purchased from Pavel Curtis. Pieces shown here.
Six Piece Ball
Six-piece ball
(aka Faberge Knot)
Made by Lee Krasnow - mechanism is identical to the Six Tabbed Planks from Pavel Curtis.

Caged Spheres (in purpleheart wood)
Also purchased from Puzzlecraft. dovetail cube
A 4-piece cube with dovetailed pieces. Designer unknown to me.
Arjeu CT87 (Ishi $37 1/18/94) Arjeu CT87 (Ishi)
This is Arjeu's CT87.
This was designed by Oskar van Deventer. Evidently Arjeu never compensated Oskar! Tom Lensch is selling a really nice version. Myopic Doves pieces
Myopic Doves by Rick Eason.

Prickly Puzzle, designed, made, and exchanged by Simon Bexfield
The Slump Cube, designed by Ronald Kint-Bruynseels, made from Mahogany and Rosewood by Eric Fuller

Frankfort Cube pieces
This cube was included in an auction lot. I didn't recognize it at the time, but after I received the lot I realized this was a copy of the Frankfort Cube I had wanted after I saw it on Casse-Tete et Solution (scroll down to item #33).

Tease Tease
The Tease puzzle cube designed by Sam Cornwell and made from Quilted Sapelle, Wenge, and Carolina White Ash by Eric Fuller. Five pieces, and five moves to get the first piece out. Oskar's Patchwork Box - Lensch
This is Oskar's Patchwork Box, designed by Oskar van Deventer and made by Tom Lensch. Purchased from Tom at IPP 29 in SF.
Chadwick Miller Think
A vintage Think puzzle by Chadwick Miller of Massachussetts. Made in Japan. Copyright 1968.
Trickstix - Harris Caged Ball
This is Trickstix, by Harris. See U.S. Patent 2473369 - Harris 1947.
The similar cage with rotating sticks and a ball inside is a common design.
Adam's Block Puzzle Senior and Panel Puzzle
I finally obtained instances of these two in their original packaging.

Adams Oriental Puzzle
I have had this small plastic red, white, and blue puzzle cage since I was a kid. Its pieces are more decorated than the Trickstix. This is Adams' Locked Blocks.
Adams' Oriental Puzzle seems to be the same design (shown for reference - I don't have that).

Molecule - Joe Miller
The Molecule by Joe Miller.
See U.S. Patent 5762336 - Miller 1998.
Entered in the IPP 2001 Design Competition.
Dragon Cube - Philos
The Dragon Cube, designed by Doug Engel. Issued by Philos. Purchased in Montreal.

Here are several offered by Bits & Pieces at various times...
Satellite - Bits and Pieces Three Bunnies - Bits and Pieces David's Flower - Bits and Pieces Contact - Bits and Pieces

Four Square - Magnif Third Dimension - Magnif Curious Cross - Magnif Curious Cross - blue
Reiss Equilibrium Reiss Torment
Several classic puzzles by Mag-Nif and Reiss that I have had since I was a kid. From Mag-Nif: Four Square, Third Dimension, and the Curious Cross in smokey plastic and blue plastic. Some 1974 Reiss puzzles: Equilibrium, Star, and Reiss' version of Curious Cross, which they call Torment.

Meiji Cheese Curls Light
Meiji Cheese Curls, and the "Light" version.
Moose Ball - Bexfield
Moose Ball - designed and
exchanged at IPP35 by Simon Bexfield

Screwy Octahedron
a 3D print designed by George Bell
Nuclear Fusion
a 3D print designed by George Bell

Stephen Chin of Australia is a skilled woodworker and woodturner. He created a beautiful apple-shaped wooden interlocking / coordinate motion puzzle he calls 1 Pinko Ringo, inspired by Wayne Daniel's 10-piece icosahedron. Stephen's puzzle was among the top 10 vote-getters in the 2010 IPP Design Competition. A similar puzzle by Stephen called the Bomb won the first Rochester Puzzle Picnic Puzzle Competition. Stephen has also created his own version of the icosahedron, known as the "Spinico." Brian Pletcher blogged about it. George Bell did some CAD modeling and after several prototypes to get the angles just right, offers spherical versions of Stephen's design in two sizes at his Shapeways shop. He calls this the Exploding Ball. The puzzle comprises 10 identical very interesting pieces. The dissection using 10 identical pieces was at first thought to be impossible to assemble, but it can be managed. Disassembly can be challenging if you cannot think of a convenient method. I bought the larger version.
Exploding Ball

At IPP35, I was able to purchase a hand-turned wooden version from Stephen:

Exploding Apple (aka 1 Pinko Ringo) - made by and purchased from Stephen Chin
One of Chinny's signature pieces. He packs it in a sock :-)
This was one of the top ten vote getters in the 2010 Nob Yoshigahara Puzzle Design Competition

Yu Gi Oh Millennium Puzzle - Bandai Hobby
The Bandai Ultimagear Yu-Gi-Oh Millennium Puzzle I had purchased arrives in its largish box packed like a model - its ABS parts are on a set of sprues. The parts must all be cut free from the sprues, carefully trimmed, and then each puzzle piece can be assembled from its constituents according to included instructions. Each of the puzzle's pieces comprises two or more parts. Fortunately no glue is required - the parts press together, albeit with some firmness needed, and I found all the fits to be satisfyingly precise and snug - the parts are very unlikely to ever be unintentionally (or even intentionally) separated. The resulting puzzle pieces are all robust and none seem prone to break during normal play while respecting the typical mechanical puzzling prohibition against use of undue force.
Millennium Puzzle - Ultimagear

Only 13 pieces left to fit in!
No instructions are included for how to assemble the puzzle from its pieces. I attempted assembly guided only by images of the finished puzzle - many times I had made some headway when I realized that I had to unwind several steps to insert a new piece, and furthermore that rotations were required! This is most definitely a sequential interlocking puzzle with rotations along the way, and I am very pleased with its overall quality. It is a bit like a plastic Berrocal - the pieces are not simply polycubes - their shapes are intricate and the placement of each is not necessarily obvious, but with patience can be deduced. Tricky and non-orthogonal movements are needed to sequentially interlock and unlock the pieces during the solve. Cutting free the parts and construction of the pieces took me about three hours, and solving (assembling the puzzle) about a further two hours - there were a couple of moments where three hands would have been helpful during the solve, and I only required one hint.
Millennium Puzzle - Ultimagear

More, in wood:

Jingora Dovetail Cylinder Puzzle - Wingstoys $9.99 Dodeca Simple Star

Jingora, Dovetail (Hoi Polloi / Reiss), Cylinder (Wingstoys), Dodeca (Tensegrity Systems 1991), Simple Star (B&P?)

These two sets of "Brain Benders" from Cardinal (blue box and red box, 3 puzzles each) include a six-piece Diagonal Star, a Chuck similar to Pentangle's Woodchuck, above, a traditional 6-piece burr, a wooden version of an 18-piece puzzle similar to Mag-Nif's Third Dimension, a rods-and-pins "Nest" puzzle similar to the Arjeu Quadro, and another 12-piece chuck called "Double Cross." They are cheaply made from softer wood, and I've seen them at toy stores for $3.99 a box. Similar sets are branded by Pavillion.

Brain Benders set Brain Benders - 18 piece Brain Benders - Nest Brain Benders - Double Cross

More, in plastic:

Pussycat - Tangle Pussycat - Pussy Sticks Pussycat - Satellit black star Plex Ball - promo Cerebral Rings - Magnif Ball Coin Bank Crazy Cube Bright Brain Disco Bell Telephone Puzzle Bright Brain Mini set Russian Molecule Chadwick Miller Pocket Puzzles

This is the TenGeo Great Circle Challenge.

This is a selection of "Mighty Midget" puzzles from Mag-Nif:

Mighty Midget

Chinese burrs I got this lot of 3 of the same "Chinese Burr" in different colors, from a French auction. I gave away two and kept the green one. Normally the #1 mechanical puzzle rule is "No Force Required!" but this puzzle really requires some force for the first and later moves.

These 4 "Travel Puzzles" are from Game Kingdom: ball in cage, 6x6x6 sticks, star burr, depth charge:

Game Kingdom Travel Puzzles Travel Puzzle - Sticks and Ball Travel Puzzle - Molecule

Ms. Leone, a teacher at the local elementary school, uses puzzles in her classroom.
Last year I loaned a bunch of puzzles to her for her students to try,
and she was very kind to send me a Cyclone puzzle as a thank-you. Much appreciated!

Cyclone puzzle - Lagoon Group Holger Strøm

The Cyclone is offered by The Lagoon Group.

Interestingly, this design seems to have first appeared as a lamp!
The product IQ Light won the 2001 Danish Design Award for its packaging.
IQ Light was designed by Holger Strøm of Denmark in 1973.
It is based on a single piece or tile, various numbers of copies of which
can be interlocked to form more than 21 different shapes.
30 tiles form a triacontahedron.
In the assembly, there are 12 vertices where 5 tiles hook together, and 20 vertices where 3 tiles hook together.

You can find a template for the piece at www.craftster.org.
William Chow has a website explaining the geometry of what he calls the Celtic Tile.

Puzzle friend and renowned sculptor and mathematician George Hart has been creating beautifully symmetric, complex, and puzzling geometric assemblies for some time.
Large versions of many of George's sculptures have been installed at universities, parks, and various other public and private spaces.

You can now own a copy of one of George's beautiful designs - it's called Frabjous and is available from the folks at Artifacture in Dallas, who sent me this 6" x 6" x 6" Special Edition Frabjous, laser cut from Acrylite Radiant Acrylic. Thanks, Michael!

This type of acrylic material reflects light in different colors from different angles and provides a fascinating display of varying hues as you move around the sculpture. The puzzle sculpture comes unassembled, in a package that includes instructions, 31 S-shaped pre-notched interlocking pieces (one extra piece is thoughtfully provided), and even a pair of cotton gloves to wear during assembly, so that you can avoid getting fingerprints in hard-to-clean places! Artifacture sells direct through various online outlets (see links on their product page), including their Etsy shop. Artifacture has produced Frabjous for MoMath - the MoMath logo, and George Hart's name, are engraved on one piece. Frabjous was available at the MoMath online shop.

It took me about an hour to assemble Frabjous. I had to recover from a false start when I realized I had been careless while interweaving some of the pieces. I disassembled what I had so far and started over, being much more deliberate. The pieces lock together by friction/pressure fit using simple rectangular tabs and notches at apexes where three pieces meet - the hold is secure, but it is possible to work the pieces apart again without too much trouble. One thing I was pleased about is that though acrylic in general seems to have an unfortunate tendency to crack at angular cut-outs, I experienced no faults in any of the Frabjous pieces even after I had attached and detached them multiple times.

During my second try at putting Frabjous together I actually found that if I ignored the included instructions and instead concentrated on the five-fold symmetry of the structure, adding five pieces at a time in symmetry around the growing assembly, I could much better ensure the correct relative placement of the pieces. Something to note is that you cannot simply create a bunch of "tripods" and then expect to link them together - it is too difficult to properly interweave such sub-structures. I took photos along the way - I think you'll agree that Frabjous is a beautiful object! I can also attest that Frabjous is a puzzling challenge to assemble, and you will enjoy a nice sense of satisfaction on completing it. My wife even let me put this one on display in the family room!

Misc. Metal

Here are some interlocking irregular geometric designs made in metal.

This is a Glingle Ball Copyright 1984 R. E. Sanson I've had it a looong time, and NEVER took it apart!
Charles O. Perry's Zen	The Buffalo Nickel is clever - it is a two-piece (plus "case") interlocking. It made by George Miller, based on a design by Oskar van Deventer. Bits and Pieces marketed this nice metal version.	Impossicube - Markus Goetz (B & P)
The Lucky Clover from B and P was designed by Oskar van Deventer. It has only 4 pieces but requires many steps to assemble properly.	Gravity Well - Bits and Pieces	Double Monad (Yin-Yang) - Bits and Pieces
Butterfly - Bits & Pieces	The Ego Sculptural Puzzle is a 6-piece version of the Third Dimension style above. It was offered in a "Good Design" box by Austin Enterprises and Something Else Inc. of Akron Ohio and Ossining NY.	From Bits & Pieces, a Curly Cube, designed by Vladimir Krasnoukhov.
Entangled Fish - B & P		Great Collision, designed by Doug Engel. Purchased at IPP 29 in SF.

Misc. Figural

While most of the Irregular Assemblies are geometric shapes, some are in the form of various figures.

This is Mr. Puzzle from Bits and Pieces, which contains several different kinds of puzzles including interlocking (his feet).	A Hartley's Humpty Dumpty Egg puzzle U.S. Patent D160283 - Irving Hartley Steinhardt 1950.	This is Nanook the Polar Bear.
This is Naef's Swiss Cow or Vache Rouge. It was designed by Gerard Petremand in 1978. This version has six pieces.	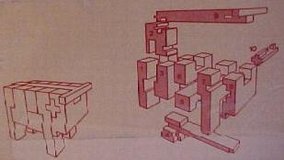This version of Vache Rouge has more pieces.
The Rhino puzzle by Theo Geerinck and Symen Hovinga at No Problem Puzzle Shop. They were inspired by Kumiki, but to me this belongs here. Note the tiny baby rhino hidden inside! I got this printed by SEA Manufacturing on Treatstock. I chose to get a black rhino.
A hand-carved wood Dragon puzzle from Thailand or Mongolia, I'm not sure.	The Sphinx (or Turtle). Getting it apart was somewhat of an ordeal, as some pieces were fused by the sloppy shellac on them - but fortunately I separated them without damaging anything.	A vintage locomotive puzzle by Reiss.
The R. B. Rice Sausage Company Pig puzzle (Lee's Summit, MO). Virtually the same pieces as Nanook, but smaller and less dense.	Cicada by Kathy Bass Available from Mr. Puzzle Australia (Brian Young). Obtained at NYPP 2008.	From William Waite, the Camera Conundrum.
Toaster - by William Waite - one of his original run, not a Pelikan remake
	An interlocking Stegosaur
I bought this aluminum Russian 1980 Olympics Bear Puzzle from a seller located in Belarus. I do not know who made it. It stands about 14cm tall and is an interlocking sculpture of 16 pieces. Like much Soviet architecture, it is blocky and brutalist - but I like it a lot! I call it a "Russian Bear-o-cal." Ha, ha! I crack myself up.

The Puzzle Sculptures of Miguel Berrocal

The Spanish sculptor Miguel Berrocal has produced many wonderful artworks, including puzzle sculptures coveted by collectors.

Berrocal was born in Malaga, Spain, in 1933, and died in 2006. He was married to Princess Cristina, the grand-daughter of the last King of Portugal. He presided over a 200-employee foundry in Negrar and referred to himself jokingly as the "boss of the sculptor's Mafia."

Probably the first time I heard of the puzzle sculptures of Miguel Berrocal was upon reading about them in one of Martin Gardner's columns in Scientific American. (Gardner discusses them in Chapter 18 of his book Penrose Tiles to Trapdoor Ciphers.) In college I had occasion to visit a friend - she was a foreign exchange student staying with an American family (hi Fariba!). The family owned a Berrocal Mini-David and that was my first opportunity to try one of the puzzle sculptures of Miguel Berrocal.

Berrocal made six sculptures in his "Mini" series, and offered them as limited edition "multiples." They include:

Mini-David
Mini-Maria
Mini-Cariatide

Portrait de Michele
Mini-Zoraida
Mini-Cristina

I have seen a variety of costs - the set of six has been offered for anywhere from $5K to $10K. Mini-David is the most popular and runs anywhere from $1K to $2.5K. The others run from $350 to $1800 depending on where you look and how lucky you get. Asking prices are on the rise. John Rausch and James Dalgety are two dealers. Read about Berrocal on Dalgety's site.

James Strayer has quite a collection of Berrocals, as does John Rausch.

Portrait de Michele (My favorite...)
Mini Maria
Mini-Zoraida
Mini-David	Mini-Cristina	Mini-Cariatide

Berrocal produced a series of Micro Pendants including Micheline-X in 1975-76 having 23 pieces, the 1973 Micro Maria having 23 pieces, the 1971 Micro David having 17 pieces, and Micro Mento 1977 which is not a puzzle (not shown). You can read about fellow puzzle collector Roxanne Wong's quest for the micros in the March 2015 post on her blog.

I am pleased to have obtained a bargain on Micheline X. It is a wearable rendition of his Portrait de Michele mini multiple - my favorite of the minis. A fairly large number of these were made, a few in gold, silver, and stainless, and most (according to the accompanying booklet) - including mine - in nickel-plated base metal (in auction descriptions often said to be chromed brass). It is surprisingly small but also surprisingly detailed. I have read that one sold for $750 back in the late 1970s - I have seen recent auction prices ranging from $350 to near $2000. I was lucky and won mine for just over $200!

Micheline X - Berrocal

Micheline X - Miguel Berrocal 1976
Chromed base metal.
23 pieces. (You see only 22 because the base screw shown in the last row, second from right, is composed of two inseparable parts.)
Came with two small booklets - an instruction book, and a compendium of Berrocal's multiples. Mine is missing its certificate.
Can you tell where I'd gone wrong in my reassembly photo?

Here is a comparison with Portrait de Michele - Micheline is sitting atop my one-kilogram cube of Tungsten:

Micheline X with Portrait de Michele

Micro David Off - Berrocal 1971
Brass version.
Shown: images of the front and back, pieces, and comparisons with Micheline-X and Mini David.

Micro David-Off - Berrocal 1971

With this instance of Berrocal's Micro Maria, I have completed the trio of Berrocal's Micro puzzles (the fourth Micro is not a puzzle).

Berrocal Micro Maria

Micro Maria with Mini Maria:

Berrocal Micro Maria

1 A A A [p] 1 0 +----+----+----+----+----+----+ / /\| + + \| / / + +----+----+----+----+----+----+ \| \| \| \| \| \| + + + / \| \| + \| \|/ +----+----+----+----+----+----+ The Key
All six positions and widths of a single slot...
18 B B L [p] 2 0 +----+ +----+----+----+----+ / /\| / /\| + + \| + + \| / / +-/ / + +----+ / +----+----+----+----+ \| \| \| + \| \| \| \| \|/ \| \| + + +----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ Local Mail	35 C E 1 0 +----+----+ +----+----+----+ / /\| / /\| + + \| + + \| / / +-/ / + +----+----+ / +----+----+----+ \| \| \| + \| \| \| \| \|/ \| \| + + +----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ Out of Town Mail	52 D P J [p] 2 0 +----+ +----+----+----+ / /\| / /\| + + \| + + \| / / +----+-/ / + +----+ / +----+----+----+ \| \| \| + \| \| \| \| \|/ \| \| + + +----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ The Side Tray	103 F S H 1 1 +----+----+ +----+----+ / /\| / /\| + + \| + + \| / / +---+--/ / + +----+----+ / +----+----+ \| \| \| + \| \| \| \| \|/ \| \| + + +----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ The Half-Tray	120 G U 1 1 +----+ +----+----+ / /\| / /\| + + \| + + \| / / +----+---+--/ / + +----+ / +----+----+ \| \| \| + \| \| \| \| \|/ \| \| + + +----+----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ The Three-Quarters Tray	256 J X B [p2] 3 2 +----+ +----+ / /\| / /\| + + \| + + \| / / +----+----+----+-/ / + +----+ / +----+ \| \| \| + \| \| \| \| \|/ \| \| + + +----+----+----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ The Tray
Three possible dual slots...			Three symmetric pieces...
86 E H 1 0 +----+ +----+ +----+----+ / /\| / /\| / /\| + + \| + + \| + + \| / / +-/ / +-/ / + +----+ / +----+ / +----+----+ \| \| \| + \| \| + \| \| \| \| \|/ \| \|/ \| \| + + +----+ +----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ The Mailbox	154 H K I [p] 1 1 +----+ +----+----+ +----+ / /\| / /\| / /\| + + \| + + \| + + \| / / +-/ / +-/ / + +----+ / +----+----+ / +----+ \| \| \| + \| \| + \| \| \| \| \|/ \| \|/ \| \| + + +----+ +----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ The Toaster	188 I M M [p] 2 1 +----+ +----+ +----+ / /\| / /\| / /\| + + \| + + \| + + \| / / +----+-/ / +-/ / + +----+ / +----+ / +----+ \| \| \| + \| \| + \| \| \| \| \|/ \| \|/ \| \| + + +----+----+ +----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ The (Bottle) Opener	871 M T K 2 0 +----+----+ +----+----+ / /\| / /\| + + \| + + \| / / +----+-/ / + +----+----+ / +----+----+ \| \| \| +----+--\| \| \| \| \| \| \| \| + + + \| + + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ The Barbells	928 V L D 2 1 +----+ +----+----+ +----+ / /\| / /\| / /\| + + \| +----+----+ \| + + \| / / +--\| \| +-/ / + +----+ / \| \|/ +----+ \| \| \| + + + \| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ The Tongue	1024 Y Y F [p2] 3 1 +----+ +----+ / /\| / /\| + + \| + + \| / / +----+----+----+-/ / + +----+ / +----+ \| \| \| + +----+----+ \| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ The Y
There are six pairs of mirror image pieces...
359 L F 1 0 +----+----+----+ +----+----+ / /\| / /\| + +----+ \| + + \| / /\| \| +-/ / + +----+----+ \| \|/ +----+----+ \| \| \| + +--\| \| \| \| \| \| \| \| + + + \| + + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+	615 K G 1 0 +----+----+ +----+----+----+ / /\| / /\| + + \| +----+ + \| / / +--\| / / + +----+----+ / \| +----+----+ \| \| \| +----+ \| \| \| \| \| \| \| \| + + + \| + + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+	792 R D 2 0 +----+ +----+----+----+----+ / /\| / /\| + + \| +----+----+ + \| / / +--\| / / + +----+ / \| +----+----+ \| \| \| + + \| \| \| \| \|/ /\| \| \| + + +----+ \| + + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+	911 N C G 2 0 +----+----+----+----+ +----+ / /\| / /\| + +----+----+ \| + + \| / /\| \| +-/ / + +----+----+ \| \|/ +----+ \| \| \| + + \| \| \| \| \| \| / \| \| + + + \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+	824 T R C [p] 2 1 +----+ +----+----+----+ / /\| / /\| + + \| +----+ + \| / / +----+--\| / / + +----+ / \| +----+----+ \| \| \| + +----+ \| \| \| \| \|/ /\| \| \| + + +----+ \| + + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+	975 O Q E [p] 2 1 +----+----+----+ +----+ / /\| / /\| + +----+ \| + + \| / /\| \| +----+-/ / + +----+----+ \| \|/ +----+ \| \| \| + +----+ \| \| \| \| \| \| / \| \| + + + \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+
The Notched Half-Trays		The Walls		The Offsets
856 S J 1 1 +----+ +----+ +----+----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +--\| \| +-/ / + +----+ / \| \|/ +----+----+ \| \| \| + + +--\| \| \| \| \|/ /\| \| \| + + +----+ \| + + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+	943 P I 1 1 +----+----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +--\| \| +-/ / + +----+----+ / \| \|/ +----+ \| \| \| +----+ + \| \| \| \| \| \| / \| \| + + + \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+	888 U W 2 1 +----+ +----+----+ / /\| / /\| + + \| + + \| / / +----+----+-/ / + +----+ / +----+----+ \| \| \| + +----+--\| \| \| \| \|/ /\| \| \| + + +----+ \| + + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+	1007 Q V 2 1 +----+----+ +----+ / /\| / /\| + + \| + + \| / / +----+----+-/ / + +----+----+ / +----+ \| \| \| +----+----+ \| \| \| \| \| \| / \| \| + + + \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+	960 X N 2 2 +----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +-------\| \| +-/ / + +----+ / \| \|/ +----+ \| \| \| + +----+ + \| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+	992 W O [p] 2 2 +----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +--\| \| +----+-/ / + +----+ / \| \|/ +----+ \| \| \| + + +----+ \| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+
The Fingered Clubs		The Clubs		The Fingers

20 +----+ +----+----+----+----+ / /\| / /\| + + \| +----+ + \| / / +--\| / / + +----+ / \| +----+----+----+ \| \| \| + +--\| \| \| \| \|/ \| \| + + +----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ Filipiak #67	56 +----+ +----+----+----+ / /\| / /\| + + \| +----+ + \| / / +----+--\| / / + +----+ / \| +----+----+ \| \| \| + +--\| \| \| \| \|/ \| \| + + +----+----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ Triple Slide	60 +----+ +----+----+----+ / /\| / /\| + + \| + +----+ + \| / / +----+-/ /\| / / + +----+ / +----+ \| +----+ \| \| \| + \| \| +--\| \| \| \| \|/ \| \|/ \| \| + + +----+----+ +----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ UBS.1	64 +----+ +----+----+----+ / /\| / /\| + + \| +----+----+ + \| / / +----+--\| / / + +----+ / \| +----+ \| \| \| + +----+--\| \| \| \| \|/ \| \| + + +----+----+----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ UBS.24	72 +----+----+----+ +----+----+ / /\| / /\| + +----+----+ \| + + \| / /\| \| +-/ / + +----+ \| \|/ +----+----+ \| \| \| +----+----+ \| \| \| \| \|/ \| \| + + +----+----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ Interrupted Slide	88 M +----+ +----+ +----+----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +--\| \| +-/ / + +----+ / \| \|/ +----+----+ \| \| \| + +----+ \| \| \| \| \|/ \| \| + + +----+----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ Piston, Hordern, Dozen, BB31-10-40
94 +----+ +----+ +----+----+ / /\| / /\| / /\| + + \| + + \| +----+ + \| / / +-/ / +--\| / / + +----+ / +----+ / \| +----+ \| \| \| + \| \| + +--\| \| \| \| \|/ \| \|/ \| \| + + +----+ +----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ Triple Slide	109 +----+----+ +----+----+ / /\| / /\| + +----+ +----+ + \| / /\|----\| / / + +----+----+----+ \| \| +----+ \| \| \| + +--\| \| \| \| \|/ \| \| + + +----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ BCL6000	112 +----+----+ +----+----+ / /\| / /\| + +----+ \| +----+ + \| / /\| \| +-------\| / / + +----+ \| \|/ \| +----+ \| \| \| +----+ +--\| \| \| \| \|/ \| \| + + +----+----+----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ Interrupted Slide	124 +----+ +----+----+ / /\| / /\| + + \| +----+----+ + \| / / +----+-/ /\| / / + +----+ / +----+ \| +----+ \| \| \| + \| \| +--\| \| \| \| \|/ \| \|/ \| \| + + +----+----+ +----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ UBS.22	126 +----+ +----+----+ / /\| / /\| + + \| +----+ +----+ + \| / / +-/ /\|----\| / / + +----+ / +----+ \| \| +----+ \| \| \| + \| \| + +--\| \| \| \| \|/ \| \|/ \| \| + + +----+ +----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ STC#36	216 +----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+ \| +----+ + \| / / +--\| \| +-/ / + +----+ / \| \|/ +----+----+ \| \| \| + +----+ \| \| \| \| \|/ \| \| + + +----+----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ Eight is Enough
128 +----+ +----+----+ / /\| / /\| + + \| +----+ + \| / / +------------\| / / + +----+ / \| +----+ \| \| \| + +--\| \| \| \| \|/ \| \| + + +----+----+----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ Hedgehog, Kaldeway, UBS.15	240 +----+----+ +----+ / /\| / /\| + +----+ \| + + \| / /\| \| +----+----+-/ / + +----+ \| \|/ +----+ \| \| \| +----+ \| \| \| \| \|/ \| \| + + +----+----+----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ Avenger (pc. #4)	156 +----+ +----+----+ +----+ / /\| / /\| / /\| + + \| +----+ + \| + + \| / / +--\| / / +-/ / + +----+ / \| +----+ / +----+ \| \| \| + +--\| \| + \| \| \| \| \|/ \| \|/ \| \| + + +----+----+ +----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ Triple Slide	160 M +----+ +----+----+ +----+ / /\| / /\| / /\| + + \| +----+----+ \| + + \| / / +--\| \| +-/ / + +----+ / \| \|/ +----+ \| \| \| + +----+----+ \| \| \| \| \|/ \| \| + + +----+----+----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ (many)	192 M +----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +----+--\| \| +-/ / + +----+ / \| \|/ +----+ \| \| \| + +----+ \| \| \| \| \|/ \| \| + + +----+----+----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ #G, UBS.17	224 M +----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +--\| \| +----+-/ / + +----+ / \| \|/ +----+ \| \| \| + +----+ \| \| \| \| \|/ \| \| + + +----+----+----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+ JVK, Millable 5.4, UBS.14
327 N +----+----+----+ +----+----+ / /\| / /\| + +----+ \| + + \| / /\| \| +-/ / + +----+----+ \| \|/ +----+----+ \| \| \| + + \| \| \| \| \| \| / \| \| + + + \| +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ IPL5S.39 1	551 N +----+----+ +----+----+----+ / /\| / /\| + + \| +----+ + \| / / +--\| / / + +----+----+ / \| +----+----+ \| \| \| + + \| \| \| \| \|/ /\| \| \| + + +----+ \| + + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+ BC-L5N, IPL5S.45 1	344 N +----+ +----+ +----+----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +--\| \| +-/ / + +----+ / \| \|/ +----+----+ \| \| \| + + + \| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ IPL5S.25 2	687 N +----+----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +--\| \| +-/ / + +----+----+ / \| \|/ +----+ \| \| \| + + + \| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+ IPL5S.33 1	376 N +----+ +----+----+ / /\| / /\| + + \| + + \| / / +----+----+-/ / + +----+ / +----+----+ \| \| \| + +----+ \| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ IPL5S.21 1	751 N +----+----+ +----+ / /\| / /\| + + \| + + \| / / +----+----+-/ / + +----+----+ / +----+ \| \| \| + +----+ \| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+ IPL5S.05 1
410 +----+ +----+----+ +----+ / /\| / /\| / /\| + + \| + + \| + + \| / / +-/ / +-/ / + +----+ / +----+----+ / +----+ \| \| \| + \| \| + \| \| \| \| \|/ \| \|/ \| \| + + +----+----+ +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ UBS.2	412 N +----+ +----+----+ +----+ / /\| / /\| / /\| + + \| +----+ + \| + + \| / / +--\| / / +-/ / + +----+ / \| +----+ / +----+ \| \| \| + + \| \| + \| \| \| \| \|/ /\| \| \|/ \| \| + + +----+ \| + +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ (many), UBS.23, IPL5S.53 1	670 N +----+ +----+----+ +----+ / /\| / /\| / /\| + + \| + +----+ \| + + \| / / +-/ /\| \| +-/ / + +----+ / +----+ \| \|/ +----+ \| \| \| + \| \| + + \| \| \| \| \|/ \| \| \| / \| \| + + +----+ + \| +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+ IPL5S.40 1	414 +----+ +----+----+ +----+ / /\| / /\| / /\| + + \| + +----+ \| + + \| / / +-/ /\| \| +-/ / + +----+ / +----+ \| \|/ +----+ \| \| \| + \| \| +----+ \| \| \| \| \|/ \| \|/ \| \| + + +----+----+----+----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ UBS.3	416 M +----+ +----+----+ +----+ / /\| / /\| / /\| + + \| +----+----+ \| + + \| / / +--\| \| +-/ / + +----+ / \| \|/ +----+ \| \| \| + + +----+ \| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ UBS.20	442 +----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+ + \| + + \| / / +-/ / +-/ / + +----+ / +----+----+ / +----+ \| \| \| + \| \| + \| \| \| \| \|/ \| \|/ \| \| + + +----+----+ +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ UBS.4
444 N +----+ +----+ +----+ / /\| / /\| / /\| + + \| + + \| + + \| / / +----+-/ / +-/ / + +----+ / +----+ / +----+ \| \| \| + +--\| \| + \| \| \| \| \|/ /\| \| \|/ \| \| + + +----+ \| + +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ UBS.18, IPL5S.49 1	734 N +----+ +----+ +----+ / /\| / /\| / /\| + + \| + + \| + + \| / / +-/ / +----+-/ / + +----+ / +----+ / +----+ \| \| \| + \| \| +----+ \| \| \| \| \|/ \| \| \| / \| \| + + +----+ + \| +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+ IPL5S.10 1	448 M +----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +----+--\| \| +-/ / + +----+ / \| \|/ +----+ \| \| \| + +----+----+ \| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ Interrupted Slide, UBS.12	736 M +----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +--\| \| +----+-/ / + +----+ / \| \|/ +----+ \| \| \| + +----+----+ \| \| \| \| \|/ /\| / \| \| + + +----+----+ \| +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+ BCL6000, #G	463 N +----+----+----+ +----+ / /\| / /\| + +----+ \| + + \| / /\| \| +----+-/ / + +----+----+ \| \|/ +----+ \| \| \| + + \| \| \| \| \| \| / \| \| + + + \| +----+----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ Tenyo Brother, IPL5S.24 1	568 N +----+ +----+----+----+ / /\| / /\| + + \| +----+ + \| / / +----+--\| / / + +----+ / \| +----+----+ \| \| \| + + \| \| \| \| \|/ /\| \| \| + + +----+----+ \| + + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+ IPL5S.34 1
464 +----+----+----+ +----+ / /\| / /\| + +----+----+ \| + + \| / /\| \| +----+-/ / + +----+ \| \|/ +----+ \| \| \| +----+ + \| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ Brown's	576 +----+ +----+----+----+ / /\| / /\| + + \| +----+----+ + \| / / +----+--\| / / + +----+ / \| +----+ \| \| \| + + +--\| \| \| \| \|/ /\| / \| \| + + +----+----+ \| +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+ D. Kriz II	474 +----+ +----+ +----+ / /\| / /\| / /\| + + \| + +----+ + + \| / / +-/ /\|-+-/ / + +----+ / +----+----+ \| +----+ \| \| \| + \| \| + \| \| \| \| \|/ \| \|/ \| \| + + +----+----+ +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ UBS.26	476 +----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+----+ + + \| / / +--\| / /\|-+-/ / + +----+ / \| +----+ \| +----+ \| \| \| + + \| \| + \| \| \| \| \|/ /\| \| \|/ \| \| + + +----+ \| + +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ Prog. Nightmare, UBS.21	702 +----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+----+ \| + + \| / / +-/ /\| \| +-/ / + +----+ / +----+ \| \|/ +----+ \| \| \| + \| \| + + \| \| \| \| \|/ \| \| \| / \| \| + + +----+ + \| +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+ BC-CCU10, Mega-6	478 +----+ +----+ +----+ / /\| / /\| / /\| + + \| + + \| + + \| / / +-/ / +----+-/ / + +----+ / +----+ / +----+ \| \| \| + \| \| + \| \| \| \| \|/ \| \|/ \| \| + + +----+----+----+----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ UBS.16
480 N +----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +--\| \| +----+-/ / + +----+ / \| \|/ +----+ \| \| \| + + + \| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ UBS.13, IPL5S.23 3	704 N +----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +----+--\| \| +-/ / + +----+ / \| \|/ +----+ \| \| \| + + + \| \| \| \| \|/ /\| / \| \| + + +----+----+ \| +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+ (many), IPL5S.32 2	495 N +----+----+ +----+ / /\| / /\| + + \| + + \| / / +----+----+-/ / + +----+----+ / +----+ \| \| \| +----+ \| \| \| \| \| \| / \| \| + + + \| +----+----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ IPL5S.20 1	632 N +----+ +----+----+ / /\| / /\| + + \| + + \| / / +----+----+-/ / + +----+ / +----+----+ \| \| \| + +--\| \| \| \| \|/ /\| \| \| + + +----+----+ \| + + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+ IPL5S.06 1	499 +----+ +----+ / /\| / /\| + +----+ +----+----+ + \| / /\|-+-/ / + +----+----+ \| +----+----+----+ \| \| \| +--\| \| \| \| \| \| \| \| + + + \| + + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ BC-CC5H	757 +----+ +----+ / /\| / /\| + +----+----+ +----+ + \| / /\|-+-/ / + +----+----+----+ \| +----+----+ \| \| \| +--\| \| \| \| \| \| \| \| + + + \| + + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+ Prog. Nightmare
506 +----+ +----+ / /\| / /\| + + \| +----+----+ + + \| / / +-/ /\|-+-/ / + +----+ / +----+----+ \| +----+ \| \| \| + \| \| + \| \| \| \| \|/ \| \|/ \| \| + + +----+----+ +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ UBS.19	508 M +----+ +----+ / /\| / /\| + + \| +----+ + + \| / / +----+-/ /\|-+-/ / + +----+ / +----+ \| +----+ \| \| \| + +--\| \| + \| \| \| \| \|/ /\| \| \|/ \| \| + + +----+ \| + +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ UBS.11	511 +----+ +----+ / /\| / /\| + +----+ + + \| / /\|-+----+----+-/ / + +----+----+ \| +----+ \| \| \| +----+ \| \| \| \| \| \| / \| \| + + + \| +----+----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ Interrupted Slide, #D, F#73	760 +----+ +----+ / /\| / /\| + + \| +----+ + \| / / +----+----+-/ / + +----+ / +----+----+ \| \| \| + +--\| \| \| \| \|/ /\| \| \| + + +----+----+ \| + + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+ Baffling, Brother	512 N +----+ +----+ / /\| / /\| + + \| + + \| / / +----+----+----+-/ / + +----+ / +----+ \| \| \| + +----+ \| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+ (many), UBS.8, IPL5S.19 1	768 N +----+ +----+ / /\| / /\| + + \| + + \| / / +----+----+----+-/ / + +----+ / +----+ \| \| \| + +----+ \| \| \| \| \|/ /\| / \| \| + + +----+----+ \| +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+ (many), IPL5S.04 1
564 +----+ +----+----+----+ / /\| / /\| + + \| + + \| / / +----+-/ / + +----+ / +----+----+----+ \| \| \| + \| \| \| \| \|/ \| \| + + +----+----+----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+ Tenyo Brother	624 +----+----+ +----+----+ / /\| / /\| + +----+ \| +----+ + \| / /\| \| +----+--\| / / + +----+ \| \|/ \| +----+ \| \| \| +----+ +----+--\| \| \| \| \|/ /\| / \| \| + + +----+----+ \| +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+ BC-CCU10	800 +----+ +----+----+----+----+ / /\| / /\| + + \| +----+----+----+ + \| / / +--\| / / + +----+ / \| +----+ \| \| \| + + +--\| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ Brown's	820 +----+ +----+----+----+ / /\| / /\| + + \| + + \| / / +----+-/ / + +----+ / +----+----+----+ \| \| \| + +--\| \| \| \| \|/ /\| \| \| + + +----+ \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ STC#36	832 +----+ +----+----+----+ / /\| / /\| + + \| +----+----+ + \| / / +----+--\| / / + +----+ / \| +----+ \| \| \| + +----+ +--\| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ Brown's, G4	976 +----+----+----+ +----+ / /\| / /\| + +----+----+ \| + + \| / /\| \| +----+-/ / + +----+ \| \|/ +----+ \| \| \| +----+ +----+ \| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ D. Kriz II, Enigma, #G
880 +----+----+ +----+----+ / /\| / /\| + +----+ \| +----+ + \| / /\| \| +----+--\| / / + +----+ \| \|/ \| +----+ \| \| \| +----+----+----+--\| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ Dubois/Gaby	883 +----+ +----+----+ / /\| / /\| + +----+ +----+ + \| / /\|-+-/ / + +----+----+ \| +----+----+----+ \| \| \| +--\| \| \| \| \| \| \| \| + + + \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ BC-CCU10	896 +----+ +----+----+ / /\| / /\| + + \| +----+ + \| / / +----+----+--\| / / + +----+ / \| +----+ \| \| \| + +----+----+--\| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ Avenger (pc. #2)	1008 +----+----+ +----+ / /\| / /\| + +----+ \| + + \| / /\| \| +----+----+-/ / + +----+ \| \|/ +----+ \| \| \| +----+----+----+ \| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ (many)	909 +----+----+----+----+ +----+ / /\| / /\| + +----+ \| + + \| / /\| \| +-/ / + +----+----+----+ \| \|/ +----+ \| \| \| + + \| \| \| \| \|/ / \| \| + + +----+ +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ Tenyo Brother	922 +----+ +----+----+ +----+ / /\| / /\| / /\| + + \| + + \| + + \| / / +-/ / +-/ / + +----+ / +----+----+ / +----+ \| \| \| + \| \| + \| \| \| \| \|/ \| \|/ \| \| + + +----+----+----+----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ Piston
926 +----+ +----+----+ +----+ / /\| / /\| / /\| + + \| + +----+ \| + + \| / / +-/ /\| \| +-/ / + +----+ / +----+ \| \|/ +----+ \| \| \| + \| \| + + \| \| \| \| \|/ \| \|/ / \| \| + + +----+----+ +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ BC-CC5H	927 +----+ +----+----+ +----+ / /\| / /\| / /\| + +----+----+----+ \| + + \| / /\| \| +-/ / + +----+----+ \| \|/ +----+ \| \| \| + + \| \| \| \| \| \| / \| \| + + + \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ Tenyo Brother	956 +----+ +----+ +----+ / /\| / /\| / /\| + + \| + + \| + + \| / / +----+-/ / +-/ / + +----+ / +----+ / +----+ \| \| \| + +--\| \| + \| \| \| \| \|/ /\| \| \|/ \| \| + + +----+ \| +----+----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ Prog. Nightmare, BC-CC4H	990 +----+ +----+ +----+ / /\| / /\| / /\| + + \| + + \| + + \| / / +-/ / +----+-/ / + +----+ / +----+ / +----+ \| \| \| + \| \| +----+ \| \| \| \| \|/ \| \|/ / \| \| + + +----+----+ +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ Interrupted Slide	984 +----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+ \| +----+ + \| / / +--\| \| +-/ / + +----+ / \| \|/ +----+----+ \| \| \| + + +--\| \| \| \| \|/ /\| \| \| + + +----+ \| + + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ Avenger (pc. #7)	996 +----+----+ +----+ / /\| / /\| + +----+ \| +----+----+ + \| / /\| \| +-/ / + +----+ \| \|/ +----+----+----+ \| \| \| +----+--\| \| \| \| \|/ /\| \| \| + + +----+ \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ Baffling
1015 +----+ +----+ / /\| / /\| + +----+ +----+ + \| / /\|-+----+-/ / + +----+----+ \| +----+----+ \| \| \| +----+--\| \| \| \| \| \| \| \| + + + \| + + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ (many)	1016 +----+ +----+ / /\| / /\| + + \| +----+ + \| / / +----+----+-/ / + +----+ / +----+----+ \| \| \| + +----+--\| \| \| \| \|/ /\| \| \| + + +----+ \| + + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ Tenyo Brother	1021 +----+ +----+ / /\| / /\| + +----+----+ + + \| / /\|-+----+-/ / + +----+----+----+ \| +----+ \| \| \| +----+ \| \| \| \| \|/ / \| \| + + +----+ +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ Prog. Nightmare	1023 +----+ +----+ / /\| / /\| + +----+ + + \| / /\|-+----+----+-/ / + +----+----+ \| +----+ \| \| \| +----+----+ \| \| \| \| \| \| / \| \| + + + \| +----+ + / \| \| +----+--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ Teufelsknoten Schlüsselanhänger	1933 N +----+----+----+----+ +----+ / /\| / /\| + +----+ \| + + \| / /\| \| +-/ / + +----+----+----+ \| \|/ +----+ \| \| \| + + \| \| \| \| \|/\| / \| \| + + +----+ \| +----+ + / \| \| + +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+ Avenger (pc. #9), IPL5S.38 1	2836 N +----+ +----+----+----+----+ / /\| / /\| + + \| +----+ + \| / / +--\| / / + +----+ / \| +----+----+----+ \| \| \| + + \| \| \| \| \|/ /\| \| \| + + +----+ \| +----+ + / \| \| +----+ \| \| + \| \|/ \| \|/ +----+----+ +----+----+ IPL5S.44 1

160 M +----+ +----+----+ +----+ / /\| / /\| / /\| + + \| +----+----+ \| + + \| / / +--\| \| +-/ / + +----+ / \| \|/ +----+ \| \| \| + +----+----+ \| \| \| \| \|/ \| \| + + +----+----+----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+
88 M +----+ +----+ +----+----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +--\| \| +-/ / + +----+ / \| \|/ +----+----+ \| \| \| + +----+ \| \| \| \| \|/ \| \| + + +----+----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+	118 M +----+ +----+----+ / /\| / /\| + + \| +----+ + + \| / / +-/ /\|-+-/ / + +----+ / +----+ \| +----+----+ \| \| \| + \| \| + \| \| \| \| \|/ \| \|/ \| \| + + +----+ +----+ + / \| \| + \| \|/ +----+----+----+----+----+----+	192 M +----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +----+--\| \| +-/ / + +----+ / \| \|/ +----+ \| \| \| + +----+ \| \| \| \| \|/ \| \| + + +----+----+----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+	224 M +----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +--\| \| +----+-/ / + +----+ / \| \|/ +----+ \| \| \| + +----+ \| \| \| \| \|/ \| \| + + +----+----+----+----+ + / \| \| + \| \|/ +----+----+----+----+----+----+	399 M +----+----+----+----+ +----+ / /\| / /\| + +----+----+ \| + + \| / /\| \| +-/ / + +----+----+ \| \|/ +----+ \| \| \| + +----+ \| \| \| \| \| \| / \| \| + + + \| +----+----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+	536 M +----+ +----+----+----+----+ / /\| / /\| + + \| +----+----+ + \| / / +--\| / / + +----+ / \| +----+----+ \| \| \| + +----+ \| \| \| \| \|/ /\| \| \| + + +----+----+ \| + + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+
416 M +----+ +----+----+ +----+ / /\| / /\| / /\| + + \| +----+----+ \| + + \| / / +--\| \| +-/ / + +----+ / \| \|/ +----+ \| \| \| + + +----+ \| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+	672 M +----+ +----+----+ +----+ / /\| / /\| / /\| + + \| +----+----+ \| + + \| / / +--\| \| +-/ / + +----+ / \| \|/ +----+ \| \| \| + +----+ + \| \| \| \| \|/ /\| / \| \| + + +----+----+ \| +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+	431 M +----+----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +--\| \| +-/ / + +----+----+ / \| \|/ +----+ \| \| \| +----+----+ \| \| \| \| \| \| / \| \| + + + \| +----+----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+	600 M +----+ +----+ +----+----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +--\| \| +-/ / + +----+ / \| \|/ +----+----+ \| \| \| + +----+--\| \| \| \| \|/ /\| \| \| + + +----+----+ \| + + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+	448 M +----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +----+--\| \| +-/ / + +----+ / \| \|/ +----+ \| \| \| + +----+----+ \| \| \| \| \|/ /\| / \| \| + + +----+ \| +----+----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+	736 M +----+ +----+ +----+ / /\| / /\| / /\| + + \| +----+ \| + + \| / / +--\| \| +----+-/ / + +----+ / \| \|/ +----+ \| \| \| + +----+----+ \| \| \| \| \|/ /\| / \| \| + + +----+----+ \| +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+
491 M +----+----+ +----+ / /\| / /\| + + \| +----+ + + \| / / +-/ /\|-+-/ / + +----+----+ / +----+ \| +----+ \| \| \| +--\| \| + \| \| \| \| \| \| \| \|/ \| \| + + + \| + +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+	630 M +----+ +----+----+ / /\| / /\| + + \| +----+ + + \| / / +-/ /\|-+-/ / + +----+ / +----+ \| +----+----+ \| \| \| + \| \| +--\| \| \| \| \|/ \| \| \| \| \| + + +----+ + \| + + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+	508 M +----+ +----+ / /\| / /\| + + \| +----+ + + \| / / +----+-/ /\|-+-/ / + +----+ / +----+ \| +----+ \| \| \| + +--\| \| + \| \| \| \| \|/ /\| \| \|/ \| \| + + +----+ \| + +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+ +----+----+----+	766 M +----+ +----+ / /\| / /\| + + \| +----+ + + \| / / +-/ /\|-+----+-/ / + +----+ / +----+ \| +----+ \| \| \| + \| \| +----+ \| \| \| \| \|/ \| \| \| / \| \| + + +----+ + \| +----+ + / \| \| +--\| \| + \| \|/ \| \|/ +----+----+----+ +----+----+	1423 M +----+----+----+----+ +----+ / /\| / /\| + +----+----+ \| + + \| / /\| \| +-/ / + +----+----+ \| \|/ +----+ \| \| \| +----+----+ \| \| \| \| \| + / \| \| + + + / +----+----+ + / \| \| + \| \| + \| \|/ \| \|/ +----+----+ +----+----+----+	1513 M +----+----+ +----+ / /\| / /\| + +----+----+ + + \| / /\|-+-/ / + +----+----+----+----+ \| +----+ \| \| \| + \| \| \| \| \|/ \| \| + + +----+ +----+ + / \| \| + \| \| + \| \|/ \| \|/ +----+----+ +----+----+----+

3-piece Pagoda, edge-length 2 The 3-piece version requires a rotating piece. I don't have a wooden example, but I made a Lego 3-piece Pagoda Burr, also shown on Brickshelf. You can see more Lego versions at Maarten Steurbaut's website.
9-piece Pagoda, edge-length 3 The tiny vintage Miyako puzzle I have is a 9-piece pagoda. It does not require a rotation. The Arjeu CT31 is another example.
19-piece Pagoda, edge-length 4 I have the Arjeu CT1102 Mercurius The Arjeu CT30 is another example.	33-piece Pagoda, edge-length 5 The Arjeu CT44 is an example. I got an inexpensive smallish version from an Asian vendor.	51-piece Pagoda, edge-length 6 I have a 51-piece Pagoda issued by Bits & Pieces. The Arjeu CT80 is another example.
73-piece Pagoda, edge-length 7 I have the Arjeu CT45 a large wooden 73 piece Pagoda puzzle	99-piece Pagoda, edge-length 8 Superpagoda - made by Henry Troyer. It is quite large and made from attractive woods. Check out Henry's Etsy Shop. The Arjeu CT46 is another example of a 99-piece Pagoda (I don't have it). Creativecrafthouse.com sells 99-piece and 51-piece versions.	129-piece Pagoda, edge-length 9 Great Pagoda - an edge-9 (129 piece) Pagoda Burr. Fairly compact given its complexity, but very nicely made. Purchased from Cleverwood. Shown with edge-6, edge-5, and edge-8 examples. I don't know of anywhere else to get a 129 piece pagoda (or larger).

This small plastic red burr is one of my older puzzles - I don't recall where I got it.	Licorice Stix - Reiss (1974)	This is a small plastic burr pendant, made in China.
This set also appeared as "Dohikus." (I don't have this.)	Kaiyue Kong Ming Lock	Another plastic version from China.
A colorful wooden version, from China.

	1 (x2)	18	52 (x3)	188 (x2)	256 (x2)	824	871 (x2)	911	928 (x3)	992	1024 (x6)	NOTES
A	1		52	188							1024x3
B	1		52		256				928		1024x2
C	1		52			824				992	1024x2	uses 824+992
D	1			188x2	256						1024x2
E	1			188	256x2				928		1024x2
F	1			188	256			911			1024x2
G	1			188	256	824				992	1024	BLACK
H	1			188			871		928		1024x2	ORANGE
I	1				256x2			911	928		1024
J	1				256	824		911		992	1024	uses 824+992
K		18	52		256x2				928		1024
L		18	52		256			911			1024x2
M		18	52		256	824				992	1024	uses 824+992
N		18	52				871		928		1024x2	GREEN
O		18				824	871x2			992	1024	uses both 871
P			52x2		256x2				928x2
Q			52x2		256			911	928		1024	YELLOW
R			52x2		256	824			928	992		uses 824+992
S			52x2			824		911		992	1024	uses 824+992
T			52		256x2			911			1024x2
U			52			824	871x2		928	992		uses both 871

Smith ID	A	B	C	D	E	F	G	H	I	J	K	L	M
My ID	1	1024	824	975	911	188	103	256	154	52	928	871	18
Count	1	3	1	1	1	2	1	2	1	2	1	1	1

Here is a list of the 17 configurations employing one of E,G,Q,U,P, or S opposite A. All require an M.		There are only 5 other configurations that use M - these do not require its rotation. All are very easy. AH-YM-YY AI-VM-YY These are three solutions for the same pieces: AI-WM-YX AI-XM-WY AI-YM-WX
AE-YM-YY (There is only one AE since E uses 6 of 10 available floating cubies, and M the other 4, demanding that all the rest be Y pieces.) AG-VM-YY AG-WM-YX AG-XM-WY AG-YM-WX AQ-VM-QY AQ-WM-QX AQ-XM-OY AQ-YM-OX	AU-VM-YU AU-WM-YT AU-XM-WU AU-YM-WT AP-WM-QY AP-YM-OY AS-XM-YU AS-YM-YT

Shackman Clown - part of a fairly rare set of figures. Discussed in Slocum and Botermans' "The Book of Ingenious and Diabolical Puzzles" on page 86.
Shackman Man in a Vest - part of a fairly rare set of figures. Discussed in Slocum and Botermans' "The Book of Ingenious and Diabolical Puzzles" on page 86.
Vintage Comic Man Puzzle I was pleased to find a Shackman Comic Man puzzle in its original box. I have a similar puzzle, also in its box, but with a different label and appearance. A comparison photo is included.
Sombrero Man - I am unaware of the provenance of this puzzle. It is similar to the puzzles in the Shackman Clown series, but Jerry Slocum has kindly checked his extensive collection of vintage Shackman catalogs and cannot find any reference to these. Frank Potts believes they were made in Germany - he has a similar puzzle - an accordion-playing sailor. Jerry Slocum believes these were made in Mexico.
Soccer Man - I am unaware of the provenance of this puzzle. It is similar to the puzzles in the Shackman Clown series
Kumiki Cigar-Smoking Man - may have been made in Germany You can see further examples of different figures at Frank Potts' website.
A vintage plastic puzzle figure, made in England, called Bulbo, with its original box. Similar to the Shackman wooden figures. Fellow Kumiki collector Frank Potts tells me the box is wrong for this puzzle - but this is how I received it from England.
Kumiki Pagodas Two large and one small. With instruction sheet on very flimsy paper.
Kumiki City Hall, with instruction sheet.
Kumiki Palace
Kumiki Shrine - Yamanaka Kumiki Works Japan
Kumiki Golden Gate Bridge - Smith Novelty Co.
Kumiki Empire State Building A simple one but I really like it!
A Kumiki Pyramid.
Kumiki Space Needle - a souvenir of the 1962 World's Fair in Seattle. An iconic piece I had been after for a while. Unfortunately while it looks great, its interlocking architecture is underwhelming in comparison to the usual better-engineered Kumikis. But I do love the box art.
A nice, large Kumiki Tori Gate
Kumiki Totem Pole
Kumiki Cabin	Kumiki Cabin - another version with windows and a coin slot in the top.	Kumiki Stemmed Group - a group of three Kumiki puzzles, each with a "stem" - Saturn, Barrel, and Strawberry.
Kumiki Ball and Bat	Kumiki Bowling Pin	Kumiki Bottle
Kumiki Geta - a pair of Japanese wooden sandals
Kumiki Dragonflies	Kumiki Pistols
Kumiki Elephants - The larger piece is a beautiful and substantial wooden interlocking elephant puzzle from the Yamanaka Kumiki Works.
This Kumiki Elephant is based on the Kumiki Sphere.
Yamanaka Kumiki Works Giraffe
Yamanaka Kumiki Works Hippopotamus
Kumiki Lions with instruction sheet on very flimsy paper
Kumiki Pigs	A larger Kumiki Pig
Piglet - vintage Kumiki
I found a Kumiki Pig much larger than those I had: In this group photo it's the huge one in the back. The piglet is in the foreground, followed by the large pig and the "regular" pig.
Kumiki Dog	Kumiki Mouse	Kumiki Horse
"Bambi" - vintage Kumiki
Kumiki Cat
Kumiki Bird	Kumiki Alligator
I found a large Kumiki Alligator, shown with the small one I had:
Kumiki Cow A butcher's version marked with cuts of beef.	Kumiki Fox by Mi-Toys	Kumiki Camel by Mi-Toys
I found a Kumiki Cow design I didn't have:
Kumiki Swan by Mi-Toys	Kumiki Ladybug
Kumiki Turtle
Kumiki Kangaroo - and that's baby Joey in her pouch!
Kumiki Penguin - purchased at the Puzzle Party from premier Kumiki collector Frank Potts I am told the Penguin is a fairly rare piece.
Kumiki Monkey
Kumiki Panda - from the Yamanaka Kumiki Works, in its original package with instruction sheet.
Kumiki Tyrannosaur	Kumiki Rocking Dragon Bank
A Kumiki Train
Kumiki Trolley by Shackman with box and instruction sheet
Kumiki Trolley by Smith Novelty	Kumiki Trolley A smaller, narrower version.	Kumiki Locomotive
Kumiki Locomotive	Kumiki Motorcycle - this one is missing a few pieces	Kumiki small Jeep
A huge kumiki Motorcycle, with stand.
Large Kumiki Jeep
Kumiki Pickup Truck
Kumiki Tank - Toybox Puzzles distributed by ISHI Press.
Kumiki small Tank This small Tank puzzle along with the Gun Truck, have acquired a rich patina. I've shown the markings on the bottom in two orientations since I don't know which is correct.
Kumiki Gun Truck This "Gun Truck" along with the small Tank, have acquired a rich patina. Unfortunately my example is missing a few pieces.
Kumiki Rocket
Kumiki Flying Saucer - a simple but elegant design
Kumiki Saturn - I finally found an intact example.
Wooden Universal Puzzle Set - a vintage set of three space-themed Kumiki puzzles Complete with box and instruction sheets.
Kumiki Airplane	Vintage Kumiki Aeroplane - Japan
Kumiki Bomber
Vintage Aeroplane Block Puzzle
Kumiki Ship Only two stacks.
Kumiki Battleship Of the Kumiki ships I have, I think this one has the most interesting architecture.
Kumiki Cruiser - a classic vintage puzzle from Japan.
New Kumiki Ship - this example is a modern offering, made from monkeypod rather than Ho wood, including (poorly) photocopied instructions rather than rice paper.
Longer Kumiki Cruiser - note the lack of side panels.
Large Kumiki Battleship - I found another very nice vintage kumiki ship - this seems to be one of the more rare types. It included a box and instructions, both in good shape.
Kumiki Paddlewheeler - Yamanaka Kumiki Works
Here are some group shots of some kumiki ships:
Battlecruiser - a hard (brittle) plastic kumiki-style puzzle from Bell of England Same architecture as the wooden version.

Order 'n'	1	2	3	4	5	6	7	8	9	10
Edge Length	2	3	4	5	6	7	8	9	10	11
Pieces 2n²+1	3	9	19	33	51	73	99	129	163	201

Colin Gaughran made this 12-piece version of the Altekruse. Note the pattern of four blocks on each face.	Arjeu CT14 "Criss Cross" This is an example of the 14-piece Altekruse variant. Note the pattern of five blocks on each face.
The Xeon Molecule by Skor-Mor is a plastic, modern-looking version. I managed to find 3 separate copies - one is all blue, one is red/white/blue, and the third is red/yellow/blue. One of them even came with a solution sheet. On two of them, some of the pieces had broken fins, but the bits were included and I was able to glue them back together.	The vintage 12-piece Panel Puzzle by Adams is also a version of the Altekruse. This is also called the "Block Puzzle Senior."
This is Arjeu CT679 - I purchased it from Ishi back when they offered such things. This variation of the Altekruse puzzle uses single pin/single hole pieces, six left-handed and six right-handed. Stewart Coffin describes this variation in his book, The Puzzling World of Polyhedral Dissections.	Stewart Coffin developed and licensed the pinned version of the Altekruse puzzle which was marketed by 3M and Avalon Hill and named Frantix. Here are the 12 pieces of the plastic version of Frantix. [John Rausch's Frantix page]
Kerry Verne made this version of Stewart Coffin's Giant Steps #10 puzzle, from Sapelle. Purchased from CubicDissection. This looks like a pagoda burr, but notice the missing blocks in the inner corners. It is actually an Altekruse variant.

This is a boxed burr I got from Tom Lensch. Each face of the outer box is attached to one burr piece inside the cube. Freeing the key piece requires a trick. The burr pieces used are: #1, #256, #888, #911, #928, and #1024. The box definitely makes it easier to solve, since the faces are distinctly fitted. The mahogany wood is really beautiful.	This is a 4-piece burr in a box from Arjeu, variously known as the "Secret Box" or "Pandora's Box" (I also made a copy from Lego). It employs (2x) #792, but the other two pieces have notches where Jurg's system does not allow them (beneath positions 1,4,5, or 8).	This is the "Combustion" burr from B and P. My first became hopelessly jammed; I obtained another. According to Brian Young, both Internal Combustion and Pandora's Box are the same design, by Tadoa Muroi in the early 1990's.
Six piece caged burr Purchased at a puzzle store in Berlin during IPP31.	Six-Piece Framed Burr by miToys	Turtle's Heart - Kotani
"Life at 21" - Bits & Pieces	Burr in a Cube #1 by Jürg and Karin von Känel, their exchange at IPP20. The pieces are { 52, 256, 888/1007, 2x 1024 }. They describe this puzzle: "There are a few notchable burrs which are level 4 and unique when assembled inside a cube, but they are of lower level and not unique when assembled outside. Burr in a Cube #1 is the one with the fewest internal voids." Their website has a link to a PDF giving the solution.	This puzzle from Bits and Pieces is called Hard Core and was designed by Frans de Vreugd.
Burr in Cage 4 12, designed by Ishino made by Maurice Vigouroux, from Padauk from the French online puzzle shop Arteludes.com run by Jean-Baptiste Jacquin and Maurice Vigouroux. Level 4.12.2.1.2.2, unique solution, 9 holes. Here is a link to the Puzzle-Palace entry for Ishino's Burr in Cage 4 12 from Arteludes. Here is a link showing the pieces. The pieces are { 52, 256, 768, 1007, 2x 1024 }. Compare to von Känel's Burr in a Cube #1 above, which has 888 instead of 768.
This boxed 6-piece burr is called Quantum Entanglement. It has a unique level 48 solution.	The red puzzle is a 3-piece boxed burr called the Swiss Cube. There are two versions - easy and hard - they look the same from the outside, but their pieces are differently notched. I have both. The red and blue puzzle in a clear cube is called the U.S. Cube. It has six interlocking pieces. All created by Jurg von Kaenel.	Innowoo Cube (?)
Yin Yang - Pelikan An unusual six-piece burr inside a hollow ball. The Yin-Yang symbols are attached to the ends of the burr pieces. Purchased from Puzzlewood.de.	Nested Burr Four CubicDissection	Prisgon from Philos, designed by Markus Goetz Purchased in Prague.
This is Swirls 1, designed by Bram Cohen. Purchased from Bernhard Schweitzer at IPP 29 in SF. Four pieces in a cage - a very difficult puzzle!	Choreographed Motion, designed by Andreas Roever Purchased at IPP 29 in SF. The four pieces have angular cuts, and multiple pieces must be moved at once. Clever, and not overly difficult. Nicely made from acrylic.	This is Quintuplets, designed by Franklin Gonsalves. Purchased from Bernhard Schweitzer at IPP 29 in SF.
An inexpensive "Ball Lock" - one piece seems needlessly truncated.	"Luban Lock Box" from China, a boxed burr with 6 pieces. The pieces are 2x4x8. BurrTools says this has 98 assemblies but 18 solutions. The highest level is 10.6.1.2.2.	Doors and Drawers - designed by Michael Toulouzas, purchased from Bernhard Schweitzer
Sticks in a Cage - designed by Tom Jolly - made by Maurice Vigouroux	The Sonneveld Cubed Burr puzzle, designed by Dic Sonneveld and made by Tom Lensch 3 unusual burr pieces inside a cubic cage - rotations are required to solve. Made from Shedua, Prima Vera, and Granadillo
Five Sticks 28 designed by Stéphane Chomine, made by Eric Fuller, from Walnut (frame) and Gum (burrs). 28 moves to remove the first piece.
4 in 2 designed by Stéphane Chomine, made by Eric Fuller, from Walnut (frame) and Mahogany (burrs). 14 moves to remove the first piece, 17 for the second.
Rupture designed by Dan Fast made by Eric Fuller
Shake Something - designed by Dan Fast, made by Eric Fuller from Yellowheart and Chakte Viga with a Walnut box Extract the four pieces from the box.
Rail Box designed by Yavuz Demirhan, made by Eric Fuller from Maple, Purpleheart, and Padauk Level 18
3 Sticks Trapped designed by Stéphane Chomine, made by Eric Fuller, from Walnut (frame) and Yellowheart (burrs). Level 12.6.8.
Tribord - designed by Stéphane Chomine, made by Pelikan from Mahogany and Wenge Level 17.3.4
Moonflight, designed by Osanori Yamamoto and made by Eric Fuller, from Walnut, Mora, and Wenge. Level 20.2.5.
Padaung Rings, designed by Alfons Eyckmans and made by Eric Fuller from Tulipwood and Acrylic - it takes 24 moves to remove the first piece.	Zauberflote, designed by Gregory Benedetti. (See this design at Ishino's site.) Made by Eric Fuller, from Yellowheart and laser-cut acrylic.
Aramis, designed by Stephane Chomine and made by Eric Fuller, from acrylic and bloodwood. Level 12.11.7.12 solution.	Captain, designed by Stephane Chomine and made by Eric Fuller, from acrylic and bubinga. 34 move solution.	4 Stick 8, designed by Frank Worrell and made by Eric Fuller, from acrylic, bubinga, bloodwood, wenge, and ash. Unique level 21 solution.
Worm Inside, designed by Chi-Ren Chen and made by Eric Fuller, from acrylic and wenge.	Quads and Rings 1, designed by Yavuz Demirhan and made by Eric Fuller, from acrylic, bloodwood, and ash.	Quads and Rings 2, designed by Yavuz Demirhan and made by Eric Fuller, from acrylic, bubinga, and ash.
Carbo Cube designed by Donald Osselaer, made by Eric Fuller from Bubinga, Maple, and Acrylic Level 6.2	Gaia designed by Yavuz Demirhan, made by Eric Fuller from Walnut, Cherry, Sapele, and Acrylic Level 11.2	Vortex designed by Chi-Ren Chen, made by Eric Fuller from Maple, Bubinga, and Acrylic Level 21, with rotations
Noncsi - designed by Tamas Vanyo, made by Eric Fuller from Bubinga and Carolina Ash. 8 pieces pack into the frame in only one way and in a specific order. Level 2.3.9.7.5.
Boards and Sticks with Frame, designed by Gregory Benedetti. (See this design at Ishino's site.) Made by Eric Fuller, from Wenge, Bubinga, and Leopardwood.
Triaxe - designed by Stephane Chomine, made by Eric Fuller from Quilted Maple and Bloodwood. Three burr pieces interlock in the frame at level 24.		Triaxe - designed by Stéphane Chomine, made by Brian Menold from Maple and Wenge Level 24.2
Vectes / Ghidorah - two designs that share the same cage, made by Eric Fuller The cage is walnut, the Vectes (longer) pieces are yellowheart, and the Ghidorah pieces are canarywood. Ghidorah uses the three shorter, distinct pieces and was designed by Yavuz Demirhan. It is at level 22.3. Vectes was designed by Alfons Eyckmans and uses the three longer identical pieces. It is level 37.2.3.
The Four Piece Burr Cube, designed by Osanori Yamamoto, and made from Curly Maple and Purpleheart by Peter Wiltshire. I really like this design, and the beautiful craftsmanship makes this a much-appreciated one-of-a-kind gift!	L in Cage - designed in 2013 by Yavuz Demirhan, made from Lacewood and Cocobolo by Brian Menold at Wood Wonders Free four L-shaped pieces from the cage - level 10.2.2 A substantial size with the cage alone at over 3" tall and about 2.5" square.
Cage for Four Sticks, designed by Stephane Chomine, made by Eric Fuller from Dark Rosewood and Sycamore. Level 24.6.3.		Hourglass designed by Osanori Yamamoto. Made by Pelikan. Remove four U-shaped pieces from a frame. Purchased from Tim Rowett at NYPP2015.
Ice Pillar - designed by Osanori Yamamoto Level 30.6.3 - the first of the four pieces won't be coming free from the cage quickly!	Tower - designed by Klaas Jan Damstra, made by Pelikan from Bubinga and Walnut Level 29.2.9.6.3
Spacemine - designed by Yavuz Demirhan, made by Eric Fuller from Sapele and Imbuya		Two Pairs One - designed by Osanori Yamamoto, made by Pelikan, purchased from PuzzleMaster
Burrito - designed by Yavuz Demirhan, made by Pelikan, purchased from PuzzleMaster	Castle Hole - designed by Osanori Yamamoto, made by Pelikan, purchased from PuzzleMaster
Typhoon S1 by Osanori Yamamoto - made by Maurice Vigouroux
Galaxia - designed by Yavuz Demirhan, made by Eric Fuller, from Jatoba, Cherry, and Walnut.		Galaxy Z designed by Osanori Yamamoto, made by the Pelikan workshop, purchased from PuzzleWood.de
Wheel Lock - designed by Tzy Hung Chein, made by Brian Menold from Tambodi sapwood, Redheart, and Maple Level 15.18.14.4	Dispersion - designed by Tzy Hung Chein, made by Brian Menold from Redheart, Box Elder, and Ziricote Level 31.2.4.4	Burrbox 1 - designed by Tom Jolly, made by Brian Menold from Spalted Beech and Holly Level 8.6.10.3
Mysterious Galaxy designed by Osanori Yamamoto, made by the Pelikan workshop, purchased from PuzzleWood.de	Khamsin designed by Jos Bergmans. Four pieces and ring, made by Brian Menold from Walnut, Maple, Wenge, Redheart, and Yellowheart. PWBP 9.3.3.3	Ring Lock - designed by William Hu, made by Eric Fuller from Padauk, Maple, Walnut, Leopardwood, Yellowheart and Purpleheart [Dis]assemble the six pieces.
Pink Ivory Ring - designed by Ken Irvine, made by Tom Lensch from Pink Ivory, Maple, and Walnut.
Stan designed by Tamas Vanyo, made by the Pelikan workshop, purchased from PuzzleWood.de
Arrow - designed by William Hu made by and purchased from Pelikan. Zebrano, Wenge, Maple. Level 23.14.7
Castle designed by Tzy Hung Chein. Made by Pelikan from Oak and Mahogany.	Hive designed and made by Alfons Eyckmans, from Padauk, Moabi, and Oak. Purchased directly from Alfons.
Gates O designed by Tamas Vanyo, made by Brian Menold A Box Elder cage with Bambooo pins and 8 identical Wenge pieces. 35 moves to get the first piece out.		Trichromat designed and made by Yavuz Demirhan The 7cm cubic cage is Wenge, and there are 3 pairs of pieces, of oak, maple, and padauk. 44 moves to get the first piece out.
In Brookline I stopped in at Eureka Puzzles and found a Mixed Up cube from Philos designed by Ad van der Schagt.
Carambole No. 2 - designed by Yavuz Demirhan, made by Brian Menold, from Sycamore, Wenge, and Yellowheart.	Paquet - designed by Yavuz Demirhan, made by Brian Menold, from Red Oak and Yellowheart.
Frisbee - designed by Stephane Chomine 2012 made by Brian Menold from Hickory and Wenge. Four pieces plus two plate frame. PWBP 23.9.2.4.3	Plusminus - designed by Yavuz Demirhan 2012 made by Brian Menold from Brazilian Rosewood and Canarywood. Three pieces plus frame. PWBP 6.2.2	Optiborn - designed by Stephane Chomine and made by Brian Menold from Black Palm, Wenge, and Holly. Four pieces plus frame. Not listed at PWBP for some reason. Here is a link to Pelikan's version of Optiborn.
Acomodo - designed and made by Yavuz Demirhan 2016 from wenge and purpleheart. Four pieces plus frame. PWBP 10.2.2 Visit Yavuz' Etsy Shop Cubozone.	Quadrox - designed by Stephane Chomine 2018 and made by Brian Menold from Padauk and Red Oak. Four pieces plus frame. PWBP 29.11.11.3
Big Quadrox - designed by Stéphane Chomine, made by Pelikan from Wenge, Padouk, Acacia, Purpleheart, and Cherry Level 29.11.7.3
Think Outside the Box - designed by Tom Jolly and made by Eric Fuller from Cherry, Padauk, Maple, Yellowheart, and Purpleheart woods.
Klaas Jan 23 - designed by Klaas Jan Damstra, made by, and purchased from Brian Menold of New Jersey. Made from Redheart and Yellowheart.
Quadrant 1 - designed by Yavuz Demirhan made and exchanged at IPP35 by Eric Fuller
Mekaniko, Mekano, and Gaveta Cross designed, made by, and purchased from Yavuz Demirhan. Cleverly designed, beautifully made, substantially sized, and reasonably priced. Check out Yavuz' Etsy site Cubozone. (Gaveta Cross is not a caged burr.)		Gravity designed by Tim Alkema Beautifully made by Pelikan from Cherry, Wenge, Purpleheart, Acacia, and Padouk Extract four pieces plus a cube from the sleeve. Level 14.2.2.2
Simple Puzzle - designed by Klaas Jan Damstra, made by, and purchased from Brian Menold of New Jersey. Made from Maple and Wenge.		Saturno No. 1 - designed by Yavuz Demirhan, made by Brian Menold from Padauk and Granadillo
Painful designed by Yavuz Demirhan made by Brian Menold from Canarywood and Redheart Separate the four pieces 14 moves to free the first piece.
Four in the Vice, designed by Stephane Chomine, made from Silver Ash and Snakewood by Mr. Puzzle Australia. Exchanged by Frans de Vreugd at IPP32
Two Halves burr by Gregory Benedetti, a caged 3-board burr, made from Ash and Mora, by Eric Fuller.
Regola 4 - designed and made by Yavuz Demirhan from Sapelle and Ash
Attis - designed by Terry Smart, made by Eric Fuller from Purpleheart and Yellowheart A six-piece burr in a cage, at level 15.14.4.
Clamped Burr - designed by Logan Kleinwaks Made by Eric Fuller, from Cherry, Walnut, and Ash Level 15.3.5 A partially boxed burr - one in a series of increasingly Constrained Burrs including: Bookend (base and 1 side), Cornered, and Looped.	Blocage - designed by Stéphane Chomine, made by and purchased from Pelikan. Merbau and Apple woods.	Fenced Burr - designed and made by Yavuz Demirhan at Cubozone
Snapped Burr - designed and made by Yavuz Demirhan
Fossil Burr - designed and made by Yavuz Demirhan from Wenge and Ash woods. Level 12.2.3.2.		Fossil Burr II - designed and made by Yavuz Demirhan from Maple, Wenge, and Padauk woods. Level 9.
Two Burrs in a Corner - designed by Logan Kleinwaks, made by Eric Fuller, from Walnut (the box), Goncalo Alves, Bubinga, Cherry, Zebrawood, Masonia, Mahogany, Granadillo, Leopardwood, Canarywood, Sucapira, Padauk, and Purpleheart Twelve burr pieces pack into the box in only one way, and also form two traditional 6-piece burrs (a level-5 and a level-4) simultaneously in only one way.
Two Burrs in a Basket - designed by Logan Kleinwaks, made by Eric Fuller from Peruvian Walnut and Carolina Ash
Tortoise - designed by Alexander Haydon O�Brien Made by Pelikan, from Dark Oak, Acacia and Wenge
Knot on My Watch - designed by Alexander Haydon O�Brien Made by Pelikan, from Wenge, Maple, Cherry and American Walnut
Padlock Burr - designed by Tim Alkema, made by Eric Fuller from Sappy Cherry and Marblewood Level 24.2.8.
Mini Lock - designed by Christoph Lohe 2018, made by Pelikan from Ash and Purpleheart. Three pieces and frame. PWBP 6.7
Spiral Lock - designed by Christoph Lohe, made by Pelikan from Purpleheart, Acacia, Wenge, Padouk, Mahogany, Maple and Cherry. Five pieces plus frame. PWBP 21.3.3.2.2
Trenta - designed by Christoph Lohe 2017, made by Brian Menold from Ash and Mahogany. Three pieces and frame. PWBP	Kubikub 2 - by Yavuz Demirhan	Cross 5 designed by Yavuz Demirhan made by Brian Menold from Canarywood, Walnut and Redheart Remove five pieces from the frame. 11 moves to free the first piece.
Pox Box - designed by Yavuz Demirhan, made by Eric Fuller from Sapele and Birdseye Maple
Summer - designed by Klaas Jan Damstra, made by Brian Menold from Curly Maple, East Indian Rosewood, and Padauk. Level 14.4.2.
Top - designed by Osanori Yamamoto, made by Pelikan from Ash and Bubinga.

These are from the (defunct) French company Arjeu, which put out an extensive line of interlocking puzzles in a wide variety of shapes. Some are shown under other sections in this website, and some I do not own and show only for reference - such cases are noted.
Arjeu CT14 "Criss Cross" (Altekruse)	Arjeu CT16	Arjeu CT28
Arjeu CT666 Here is a link to a solution video on YouTube, and another in lower resolution.	Arjeu CT718 This looks like the "Eighteen Piece Double Cross" described by Edwin Wyatt in his 1946 book Wonders in Wood, on page 31.	Arjeu CT752 La Lanterne From an Ergatoudis auction
Arjeu CT753 This is made from pieces very similar to CT752 - the slots are moved out towards the board ends. (I don't have this - shown for reference.)	Arjeu CT52 "3 Keys" This is an unauthorized copy of the van der Poel 18-piece burr.	Arjeu CT117 Known as "3-4-5."
Arjeu CT757	Arjeu CT456 15 2x2x12 pieces, to be arranged in a 4x5x6 structure. Purchased from PuzzleMaster.ca.
More Arjeu, collected here in one place for convenience, though I wouldn't call all of these burrs. Some of these are shown under other sections in this website, and some I do not own and show only for reference - such cases are noted.
Arjeu CT442 (Colorado)	Arjeu CT210	Arjeu CT795 (Cactus)
This is Arjeu's Quadro (CT755)	This is Neptunus from Arjeu (CT1101). It is made of three notched plates.	This is a 4-piece burr in a box from Arjeu, variously known as the "Secret Box" or "Pandora's Box"
Arjeu CT1102 Mercurius	This is Arjeu CT679	This is Arjeu's CT87 designed by Oskar van Deventer.
Arjeu CT5152 aka Achille	Arjeu CT45 a large wooden 73 piece Pagoda puzzle	Arjeu CT109

The Missing Notch burr by Stewart Coffin, made from Canarywood, by Eric Fuller.	Double Slideways Burr - designed by Ray Stanton, made by Eric Fuller, from Maple, Walnut, and Sapele.
Camouflaged Burr - designed by Emil Askerli, made by Eric Fuller from Cherry and Walnut woods. Level 4.7.	Disguised Burr - designed by Emil Askerli, made by Eric Fuller from Cherry and Walnut woods. Level 7.2.2.
Glued, designed and made by Gregory Benedetti. Resembling a six-piece burr, this puzzle is composed of six conventional burr pieces that have been glued together in pairs. The puzzle is level 4.3 and [dis]assembly requires a rotation. It is made from Bolivian Santos Rosewood, Kingwood, Tulipwood, Bloodwood, Difu, and "Wood of Jesuit" and is very pretty. It is a nice size - the pieces are 25x25x75mm - and is quite heavy.	This is the Q Burr, designed by Jim Gooch, made by Steve Strickland, from Rosewood. Four pieces, one of which is a cube. Purchased from Steve Strickland's new website (defunct).
Murbiter's Pseudo-Burr - by Primitivo Familiar Ramos, made by Vinco. Four identical pieces and a unit cube combine to form the familiar 6-piece burr shape. A kind gift - thanks, Primitivo!
Crenal - one in a series of "New Old Style" burrs designed by Greg Benedetti, made by, and purchased from Eric Fuller. Made from Purpleheart.
Seizaine - NOS #7 - designed by Gregory Benedetti Made by Eric Fuller from Ambrosia Maple
Ordinary Burr - designed by Goh Pit Khiam and made by Tom Lensch from Yellowheart wood with Baltic Birch plywood mazes for strength. Looks like a conventional six-piece burr, but inside contains maze-following pins.	A Mazing Burr - designed by Junichi Yananose Looks like a conventional six-piece burr, but inside contains maze-following pins.
Eight Piece Burr - made by Scott T. Peterson
Augmented Burrs
P-Burr - designed by Junichi Yananose, made by Brian Young from Queensland Silver Ash and Queensland Blackbean 6 pieces, level 18.2 with a unique solution. The pieces { 856/943, 871, 960/992, 1024 } are length 8 and each has a bar attached to each end. (If you omit the end bars and substitute 911 for 943, you get the pieces used in Bill Cutler's Bin Cross.) I am proud to say I solved this one from the unassembled state unaided!	Stepping Burr - designed by Junichi Yananose, made by Brian Young at Mr. Puzzle Australia. Level 10. Thanks, Chelsea!
Brace Yourself - designed by Frans de Vreugd for IPP33, made by Brian Young at Mr. Puzzle Australia, from Papua New Guinean Rosewood. 6 pieces form an unconventionally-shaped burr. Solved this one from the unassembled state!
The Stellated Burr from Primitivo Familiar Ramos of Spain. Two copies are shown.
Hybrid Burrs
The Switchboard Burr designed by Jim Gooch and made by Eric Fuller mixes pieces from 3 different styles of burr, and its solution employs a move one does not often see. The woods are: Pau Amerillo (the yellow), Wenge (the dark), and Bocote (the brown striped).	Mixed Pieces Burr #2 - designed by Frans de Vreugd. Purchased from Frans at IPP28 in Prague.
Conjoined Burrs
Cold Fusion - designed by Logan Kleinwaks, made by Eric Fuller, from Walnut, Maple, and Cherry Four interconnected burrs, level 18.6.8.	Double Kongming Lock

The four members of the Wausau burr series by Bill Cutler - '81, '82, '83, and '84. See Allard's blog for a nice review of the Wausau burrs.
S/M24 designed by Bill Cutler, purchased from and made by Eric Fuller from Ash, Padauk, and Purpleheart. 7 moves to get the first piece out.
The Visible Burr, designed by Bill Cutler, made by Jerry McFarland, from Cherry, Maple, and Walnut woods.	This is Bill Cutler's 66-piece Cutler Cube. It is a beauty, 100mm on a side, and difficult to disassemble/reassemble.
Binary Burr - Bill Cutler	Binary Pin Burr - designed and made by Jerry McFarland
The Ternary Burr - designed by Goh Pit Khiam, made by Eric Fuller from Walnut and Cherry. 22 pieces, 75 moves to get the first piece out.
The Quadlock 1 is an interlocking burr cuboid puzzle made by Jerry McFarland from Mahogany, Walnut, and Maple, and designed by him in 1992. Purchased from Jerry. It has 19 pieces and is difficult to take apart. It is beautifully finished! You can read reviews here and here.	BurrBlock by Jerry McFarland One of Jerry's first copies of his new design, which was entered in the 2012 Design Competition. It's beautiful, hefty, and quite puzzling!
BurrNova - designed and made by Jerry McFarland. "A puzzle that solves itself." While not wholly true, Jerry's novel design incorporates magnets such that at a certain point several pieces move themselves with a satisfying clacking. BurrNova won an Honorable Mention in the 2017 IPP37 Paris Design Competition. This version was since re-designated "BurrNova 2D" as Jerry has created a followup he calls BurrNova 3D (aka Magnetic Madness), wherein hides a mermaid awaiting rescue. Magnetic Madness was among the Top Ten Vote-getters in the 2018 IPP38 San Diego Design Competition. Jerry posted a short video of its action. Kevin Sadler has a very detailed September 2017 post about BurrNova (2D) on his blog, as well as an August 2018 post about the BurrNova 3D (aka Magnetic Madness).

Lion's Claw - designed by Yavuz Demirhan, made by Brian Menold, from Bloodwood.	Forma - designed, made by, and purchased from Yavuz Demirhan of Turkey.
Queen Sixteen - designed, made by, and purchased from Yavuz Demirhan of Turkey.	Tetradyma 5x5 - designed by Yavuz Demirhan
Capsula Burr - designed by Yavuz Demirhan, made by Eric Fuller from Walnut and Maple
Hedgehog Burr - designed and made by Yavuz Demirhan from Sapelli and Maple woods. Level 16.4.	Susie Qube - designed and made by Yavuz Demirhan at Cubozone
Burrcell - designed and made by Yavuz Demirhan from Sapelle and Wenge Six burr pieces and 12 identical exterior pieces.	Nembus #2 - designed by Yavuz Demirhan, made by Brian Menold from Canarywood and Maple.
Volantis - designed, made by, and purchased from Yavuz Demirhan of Turkey. Check out what's available at Yavuz' Etsy shop Creacubes.
Transenna (improved) - designed and made by Yavuz Demirhan Allows an alternate assembly, also shown.
Oramagomaburamago - designed and made by Yavuz Demirhan

Chen's Six Board Burr Designed by Chi-Ren Chen Level 2.14.12 Made by Eric Fuller, in Walnut, Ash, and African Mahogany	Tropical Fish designed by Chi-ren Chen, made by Brian Menold from Redheart and Yellowheart A six-board burr. Level 19.5.1.1.2
Tricolore - designed by Frans de Vreugd made by Brian Menold from Padauk, Holly, and Katalox Level 3.15.11.2	Y6BB1 - designed by Yavuz Demirhan, made by Brian Menold from Tzalam, Okoume, and Mulberry Level 3.11.2.3.4
Knotty 6 - designed by Yavuz Demirhan	The Ambigram Burr, designed by Gregory Benedetti. Available from Puzzlewood.de. Made from Wenge, Padauk, and Robinia. Thanks to Bernhard Schweitzer and John Devost!
Knotted Burr - designed by Noah Prettyman Made by Eric Fuller, from Black Limba
Grooved 6 Board Burr No. 2 - Pluredro. Made from Bubinga and Beech woods. Level 25.2.3.3.
An inexpensive (and imprecisely made) 6-piece board burr. This is the same design that appeared in the French Fabbri series.
Here is one of Andrew Crowell's takes on the six piece board burr - this one is called RIPley and in usual Crowell fashion, requires rotations! Made by Brian Menold from curly maple with paduak splines.	RIPtide - a 6-plate burr requiring rotations designed by Andrew Crowell, made by Brian Menold
Bedevil designed by Yavuz Demirhan, made by Brian Menold from Redheart and Holly
Delight - designed by Stephane Chomine and made by Brian Menold from Lacewood and Bolivian Rosewood.	X Marks the Spot designed by Derek Bosch Sequentially interlace the four acrylic pieces and form the hash shape. Purchased from Creative Crafthouse.
George Miller made this version of Frans de Vreugd's "Extreme Torture" separated board burr. It takes 28 moves to free the first piece and then 21 more to free the second piece! Here is a link to the solution on George Miller's site. Here is an article at woodcentral.com by Steve Strickland about making 6-board burrs.	Thinkfun now offers an inexpensive and colorful version of the Extreme Torture puzzle. They call it "Gordian's Knot" and it includes a step-by-step reversible solution booklet. You can see a solution on Richard Whiting's site.
Sonneveld 9-piece Board Burr - made by George Miller.
Augmented Board Burrs
This is Ozone designed by Ronald Kint-Bruynseels. It is a six-board burr, with a "hook" attached to each piece. It requires 13 moves to remove the first piece, then 11 for the second. Ronald has designed several unusual burr-type puzzles, and you can see many of them at Bernhard Schweitzer's Puzzlewood site. Richard Whiting has put together a nice page at his site where you can read about several other high-level burrs.	This is Frans de Vreugd's design he used for his exchange at IPP25. Frans calls it a Plated Six-Piece Burr. Mr. Puzzle Australia called it Around the Bend. Frans says he developed it while working on Bent Board Burrs. It uses pieces 120, 154, 256, 412, 960, and 1024. Each has a 2x4 unit plate attached to its right end. It is the highest level burr of this type with notchable pieces. It is made from Queensland Silver Ash (the light wood) and Queensland Blackbean.
Dovetail Burr - designed by Frans de Vreugd Issued by Bits & Pieces A single solution, at level 6. Based on Yananose's 6-board burr.
The Zig Zag Knot, from Thinkfun. This is a nice plastic mass-produced version of Ronald Kint-Bruynseels' 2003 design he called "ZeeZee ZedZed" - see it on Ishino's site. Thanks to Tanya Thompson!	Twin Board Burr - Dawir

These small but elegant burrs are made from a special plywood, from Pacific Puzzle Works.
Knot Mass 36, designed by Oskar van Deventer. This instance is pretty small, at 36mm. It's made from a 5-ply maple core / maple-top hardwood laminate.	Tubular Burr Box (aka Space Invaders), designed by Ronald Kint-Bruynseels. This instance is pretty small, at 36mm. It's made from a 5-ply cherry / maple-top hardwood laminate.	Oskar's Egg A 3-piece ball inside a 2-piece egg. How does it come apart?
These are members of the "Quad Squad" family of burrs with interchangeable pieces, from Viktor Genel...
Quadrocube - Viktor Genel	QuadroPrizm - Viktor Genel	Long-Beamed Star - Viktor Genel
The Kuball, a 3-piece puzzle designed by Viktor Genel. Made by Tom Lensch. See the pieces at John Rausch's PuzzeWorld.
The burrs below are from a variety of sources...
Easy Livin' designed by Ronald Kint-Bruynseels Purchased from Bernhard Schweitzer at NYPP 2008 This is notable because a copy sold for $11,111 in one of Nick Baxter's auctions!
William Waite's Stellar Burr	From Davan's, a Rojo	"Numero Caro" This is an Asian copy of Oskar van Deventer's Knot 12.
T Time - Davans	Maruca - Davans	Zinato - Davans
Die in Prison (with a central puzzle box), designed by Ronald Kint-Bruynseels and made by Eric Fuller. The six pieces are made of Bubinga, and the central cubic box is made of Yellowheart.	This is Luxemburr, designed by Matti Linkola, exchanged at IPP16 - made by Eric in Yellowheart and Walnut.	Lassen Risti - made by Eric Fuller
RD001 Designed by Ronald Kint-Bruynseels and made by Eric Fuller. Gum wood and Ipe.	The Ribbon Puzzle, designed by Tom Jolly, made by Eric Fuller from Chakte Cok and Zebrawood - six pieces that form the 3-piece burr shape.
Anderson's Delusion Designed by Ronald Kint-Bruynseels. Made by Eric Fuller from Gum wood and Rosewood.	ISBR x 5 - designed by Mineyuki Uyematsu Made by Eric Fuller, from Yellowheart
This is the Tornado Burr designed in 2007 by Junichi Yananose, made by Eric Fuller from Padauk wood. Eric says, "This is one of the most difficult puzzles I've ever made. They are extremely time consuming to make, requiring many specialized jigs. I doubt I'll be making these again!" This burr, with its unusual and interesting movement, won an Honorable Mention award in the 2007 IPP Nob Yoshigahara Design Competition. Here is the Tornado Burr partially disassembled, into two halves:
Band Cube - designed by William Hu, made by Eric Fuller, from Bloodwood and Acrylic. Although it looks like a caged burr, of its seven pieces, all three of the plate pieces are open, not rings. See Band Cube at Puzzle Will Be Played.	Claw 3 - designed by Alfons Eyckmans, made by Eric Fuller from Grandillo and Sapele
Sweet 16 Burr - designed by Jack Krijnen, made by Eric Fuller	Rar - designed by Tamas Vanyo, made by Eric Fuller from Maple and Chakte-Kok woods. Level 9.15.1.6.
Accordion 3.5 - designed by William Hu, made by Eric Fuller, from Chakte Viga and White Oak.	Amatores - designed by Alfons Eyckmans, made by Eric Fuller, from Maple and Walnut.	Six Stick Burr - designed by William Hu, made by Eric Fuller, from various woods.
Boron designed by Donald Osselaer made by Eric Fuller	Gobi designed by Alfons Eyckmans made by Eric Fuller	Chicken Puzzle designed by Olexandre Kapkan made by Eric Fuller from Yellowheart and Cherry
Double Knuckles	P24 Marian's Puzzle - Drueke You can see a solution at Richard Whiting's site.	Karin's Outline Burr
Sliced Burr - Philos	Vesa Burr Simple - Philos - designed by Vesa Timonen for IPP21. A gift from Bernhard - thanks!	I found Linking Squares from Philos at The Games People Play. Linking Squares consists of 12 pieces with embedded magnets, that must be constructed into an octahedral shape composed of three interlinked rectangles. It was designed by J. Verhoeff.
I found Sheffield Steel 6BB from Philos at The Games People Play. Sheffield Steel 6BB was designed by the prolific Ronald Kint-Bruynseels - it is a six-piece burr at level 17.14.5.2.3 (see the pieces at Ishino's site; Richard Whiting describes the puzzle on his site, and gives a solution).	The Open Cube, designed by Marc van Kreveld and Theo Geerinck, produced by PuzzleWood	Apple - designed by Osanori Yamamoto, made by Pelikan. A PuzzleMaster exclusive.
The Blitz - Mr. Puzzle Australia Seems similar to the Saturn shown at Philippe Cichon's site.	Here is Sonneveld's Illegal Burr - Tom Lensch made it. It's "illegal" because a rotational move is required.	The Twisty Burr, designed by Derek Bosch and made by Tom Lensch. Purchased from Tom at NYPP 2008.
The Boston Tea Chest, from Mr. Puzzle Australia. I have one of their Craftsman Range examples in Australian Flooded Gum wood. Six pieces, with a two-step internal locking mechanism. A traditional burr-solving computer program won't help you with this one.	Decemburr - Mr. Puzzle Australia A 12-piece, level 13 burr designed by Goh Pit Khiam in December 1999 without the use of a computer.	This puzzle from Imagin is a knock-off of von Kaenel's Coated Burr idea. You can see a solution on Richard Whiting's site.
TriRods by Serhiy Grabarchuk - from Bernhard Schweitzer	Bombay Co. Angles and Edges	Yananose 2x3 Type 0
Double Cross - B&P	Coming of Age - designed and made by Vaclav Obsivac Presented at IPP27 by Laurie Brokenshire Six pieces made from every possible combination of 3 (out of 18) 1x1x5 Walnut bars, plus 8 1x1x1 blocks. The right-hand picture shows the puzzle properly assembled.
QED - Pentangle	This inexpensive Samanea (Monkeypod / Raintree) wood 12-piece burr was sold as the "Mercury Star" but it is a shrunken copy of Akio Kamei's Box and Cage design, without the box.	The Desert Rose micro-burr, designed by William Waite and made by Allan Boardman, who is well-known for crafting microscopic puzzles. It's only 1/2 inch across! Made from walnut and masur birch. Purchased from William at IPP 29 in SF.
Flange 99A, designed by Tom Jolly. Purchased at IPP 29 in SF. Laser-cut. Six pieces, only two identical. 8 moves for the first piece.	Flange 77A, designed by Tom Jolly. Purchased at IPP 29 in SF. Laser-cut. Six pieces, all identical. 4 moves for the first piece.	"Knobbly Burr" designed by Dic Sonneveld made by Brian Menold
Snookstick (aka Starburst) designed by Jean Claude Constantin issued by Bits & Pieces, as Starburst	In CFF #84 March 2011, Vesa Timonen published an article "A Travelogue to My Puzzle Designs" where he describes the genesis of several designs including the 1998 6-piece Timonen's Burr.	456 Burr Almost identical to the Arjeu 456 Burr (I don't have this - sold at NYPP2012.)
Heart to Heart This is similar, but not identical, to Timonen's Vesa Burr.	A six-piece "knot" laser-cut by Steve Kelsey. Thanks, Steve!	Nur Mut from Wil Strijbos (Pic from G.S.)
36 Piece Burr - designed by Jacques Frossard, made by Maurice Vigouroux This has only eight holes inside. It has one solid key piece, but without using piece coloring constraints, even BurrTools cannot solve it!	Burr Cube by unknown designer - made by Maurice Vigouroux from Caroline (Loblolly) Pine
Phelan, designed by Alfons Eyckmans. A non-traditional 18-piece burr, made by Maurice Vigouroux, from Walnut. Purchased from the French online puzzle shop Arteludes.com run by Jean-Baptiste Jacquin and Maurice Vigouroux. Ishino shows the pieces, and indicates Phelan is level 17.1.16.8. 5.16.2.8...	Vinco 4 Piece Burr made by Brian Menold
Hyperboloid Burr, designed by Oskar van Deventer and Naoaki Takashima, made by Kanagawa Toy Co. Ltd., exchanged by Naoaki Takashima at IPP32		John Rausch calls this one the 12 piece Twist Burr, and lists the designer as unknown. My copy is a cheap one from Asia.
IPP Burr - Mr. Puzzle Australia	Triade, designed and exchanged by Andreas Röver, made by New Pelikan Workshop	Brandenburg Gate designed by Jos Bergmans requires rotations produced by Puzzlewood.de
Dragon Puzzle with Washington Monument, designed, made, and exchanged by Zandraa Tumen-Ulzii at IPP32	Knobbly Box, designed by Oskar van Deventer, made by Tom Lensch, exchanged at IPP32 by Rob Jones	Lancelot - designed by Stephane Chomine, made by Pelikan, purchased from PuzzleMaster
SIXI Cube by Vinco. Assemble the six unique pieces. A nice sequential interlocking puzzle.
CEI Burr - designed by Gregory Benedetti 12 unusual pieces. Disassembly appears easy at first, but beware! From Bernhard Schweitzer at Puzzlewood.de. Thanks, Bernhard!
3-Board-Burr Quartet - designed by Mineyuki Uematsu Purchased from eBay seller Cu-Japan
The By George Burr - designed by George Syriaque in 2011, and entered in the 2012 IPP Design Competition. Its six unusual pieces serially interlock. George kindly sent me a prototype made by Brian Menold - thanks, George!
Colin Gaughran's 12-piece Burr I had the opportunity to visit Colin's workshop in Lyme and we had a fun discussion about puzzles and puzzle-making. I saw several works in progress destined for various collectors. Colin was kind enough to give me this 12-piece burr he designed and made from cherry wood. Thanks, Colin!
While taking inventory in one of my storage cabinets I re-discovered a puzzle I didn't recognize, disassembled in a bag. I posted a photo of one of the 12 identical pieces to some online forums and asked for help identifying the puzzle. Several puzzle-friends responded (thanks!), and John Devost came through, suggesting the Cubion designed by Philippe Dubois. (Also sometimes spelled Coubion.) Cubion at John Rausch's site, Coubion in Jerry Slocum's collection, Cubion in Tamura's collection, Cubion in 1999 Baxter auction where lot d7 sold for $93, Cubion in 2007 Baxter auction where lot 771 sold for $525, Cubion in 2011 Baxter auction where lot 2242 sold for $325. The Coubion is shown in Slocum's 1994 The Book of Ingenious and Diabolical Puzzles on page 75. Based on the references and images we found online I was able to reconstruct my copy. Cubion designed by Philippe Dubois, unknown provenance It fits together albeit with lots of slop. The relatively soft wood makes it easier to "squish" the pieces into place. The notches are not precisely cut and the resulting fit is imperfect but I cannot fathom any other better configuration of these pieces with their peculiar cuts. I do not know who made it - it was part of a group of wooden puzzles of unkown provenance in an auction lot I won back in December 2007. Crudely made but I give the maker props for even attempting it since the necessary angles seem so obscure! I wonder how many Cubions are out there? Had I reviewed my old What's New pages in the first place, I would have found this photo I posted back in December 2007 of the assembled form... But I still wouldn't have known the name of the puzzle.
Brackets Burr designed by Stéphane Chomine. Six pieces, made by Brian Menold from Redheart and Wenge.
This is the Vauban H5 designed by Stéphane Chomine and precisely made by Pelikan Puzzles from Bubinga and Maple. Four pieces.		Smart burr designed and made by Alfons Eyckmans from Itauba and Wenge woods 15 pieces, level 24.7.1.1. 4.1.2.3.1. 4.5.4.2 I like it because of its 'S' theme!
Thor's Hammer designed by Stephen Baumegger, purchased from and made by Pelikan, from Maple and Oak.	Covalent designed by Tamás Vanyó, purchased from and made by Pelikan, from Maple and Purpleheart.	Block - designed, made by, and purchased from Stephan Baumegger of Austria. Made from Wenge, Bubinga, and Maple. Level 7.2.2.2 See more of Stephan's designs at his Facebook page Puzzleisure.
Really Bent Board Burr - designed by Derek Bosch, made by and purchased from Johan Heyns of South Africa. Made from Pau Marfim (light) and Mansonia woods with black Ebony feathers. Johan supplies a lovely stand as well. You can contact Johan on Facebook with your requests.	Cubic Burr - designed by Tom Jolly made from Red Meranti and exchanged at IPP35 by Tim Udall
Six Piece Open Drawers - real name and designer unknown to me.		Sorcerer's Apprentice - a novel burr designed and made by Stephan Baumegger
Crosscut - designed by Dan Fast made by and purchased from Pelikan. Cherry and Wenge. Level 13.2
Hug - designed and made by Alfons Eyckmans from Vitex and Padauk Level 19	Venus - designed and made by Alfons Eyckmans from Ash and Purpleheart Level 16	Venus 4 - designed and made by Alfons Eyckmans. I've managed a partial disassembly - shown in the background is an original Venus also from Alfons.
Infinity - designed and made by Alfons Eyckmans from Ipe, Oak, Okan Level 25	Simple Sharp - designed by Stéphane Chomine	Forgotten Piece - designed and made by Marcel Gillen exchanged at IPP35 by Tania Gillen Disassemble the burr and reassemble with the extra piece inside.
Kaon - designed by Duane Einfeld, made by Eric Fuller from Sapele and Padauk Six pieces form the shape of the classic OCC burr.
Coniburr - designed by Tim Alkema, made by Eric Fuller from Ash and Padauk. Four outer pieces and four inner burr-like sticks. Level 16.
Recede - designed by Alexander Haydon O'Brien, made by Pelikan from Wenge and Cherry.
Coriolis - designed by Lucie Pauwels, made by Pelikan My copy is made from Maple and Walnut.	Silene - designed by Alfons Eyckmans Made by Brian Menold, from redheart, katalox
Pinco - designed by Erhan Cubukcuoglu Made by Eric Fuller, from Walnut, Leopardwood, Paduak, Canarywood, Maple, Tamarind, Cherry
Pisa #2 + Cubin Burr - designed by Junichi Yananose
Rota # - designed by Lucie Pauwels, made by Pelikan.
Robrecht 02 - a burr designed by Robrecht Louage, from PuzzleWood.de. Six pieces, one solution, at level 14.4.2. Thanks, Chelsea!
Burr Lock E - designed by Christoph Lohe, produced by Andrew Crowell	Moai's Tomb - produced by Andrew Crowell
Bison - designed by Jack Krijnen, made by Pelikan.
Christmas Tree - designed by Stephan Baumegger, made by Pelikan.
I long admired and have now found an example of the Japanese Wood Joint Burr, designed by Frans de Vreugd and exchanged by Frans at IPP19 in London.

This is Junichi Yananose's H-Burr, made in aluminum and purchased from Torito.	Cold Fusion, designed and exchanged at IPP32 by Oskar van Deventer, made by Shapeways	Kaiyue Ball Burr (Kong Ming Lock 30394)
Four-piece red weave	The Kray Twins designed and 3D Printed by Steve Nicholls. This unusual six-piece burr was Steve's IPP34 exchange gift. Steve kindly sent me a copy - thanks very much, Steve!	Triburrlism - designed, 3D printed, and exchanged at IPP35 by Steve Nicholls. Assemble the three pieces so the result fits in the container.
Slida - Slida website Colorful but simple.
Cube Ball - by George Bell at PolyPuzzles Form a cube from three 3D printed pieces.
Four Piece Cube - designed by Dic Sonneveld, made by Lee Krasnow from various metals. It's tiny!
Randy's Cube - designed by Randy Pearson Entered in the 2012 IPP Design Competition as "Pearson Puzzle Pieces" - 6 pieces form a cube. Purchased from e3cubestore.com
The Arch Burr in aluminum, from Bits and Pieces. Designed by Oskar van Deventer. Six pieces, square in cross-section, but curved. The pieces can be interlaced to form two "traditional" (but curved) six-piece burrs simultaneously, at the ends of the arches. There is more of Oskar's genius in the Arch Burr than may at first be apparent. The two burrs aren't exactly equal. All the pieces are symmetric in that the "traditional" burr piece that exists on each end of an arched piece is the same, except for the smallest silver piece (middle right in the photo of the pieces). On that one, the pieces on the ends are mirror images! Using my ID scheme, the large black piece at top left is a 1024/1024, the bottom left black piece is 52/52, and the upper right black piece is the key 1/1. The silver pieces on the left and in the lower right are both 1024/1024, but the right middle silver is 824/975. Oskar has realized that the two traditional six-piece burrs { 1, 52, 824, 3x1024 } and { 1, 52, 975, 3x1024 } can be juxtaposed in this arched configuration allowing the shared key to be slid into place simultaneously! Another note - when you remove the key and glance inside you will see that there is a unit cavity on each end - neither burr is truly "solid" - each has one hole that could have been filled with an extra unit cube. If the large silver piece, instead of being 1024/1024, was 960/992, the burrs would be solid and I believe could still be constructible in this dual configuration. However, the simplification of this piece by the removal of those "fingers" no doubt improved durability and reduced manufacturing complexity and cost.
Dodecafé - Rik Brouwer Purchased from Rik's Shapeways shop. Difficult to assemble and even more difficult to take apart.

4-piece Tetrahedron	5-piece Tetrahedron Padauk and Beech
Six Piece Tetrahedron - designed and made by Wayne Daniel I had been after this one for a while, to round out my set of tetrahedrons by Wayne Daniel - and it does not disappoint! Beautifully made and quite a challenge. I love it! Just look at those intricate pieces! How did Wayne manage this??
Dual Tetrahedron	5-piece Truncated Cube The Truncated Cube is surprisingly hefty, and very nicely finished. Very unusual piece shapes. Brazilian Cherry (Jatoba)
6-piece Truncated Cube Padauk	7-piece Truncated Cube Jarrah For me this has been the most difficult of the three truncated cubes.
Golden Rhombic Icosahedron	Sequential Truncated Octahedron Maple
I found a Tigerwood version of Wayne Daniel's Golden Rhombic Icosahedron. I already had another version I believe to be the IPP17 exchange gift from Abel Garcia, made from Chechin wood. They have different pieces. John Rausch describes the full set on his PuzzleWorld website. Each puzzle has only four pieces, but they are difficult to take apart and to assemble. The Zebrawood version has a slightly rounded interior edge to permit [dis]assembly.
Twelve Bowties 2 - designed and made by Wayne Daniel exchanged at IPP35 by Marti Reis
This puzzle is called Pulsar. It is based on a design by Victor Genel, modified by Benji and Ginda Fisher, and served as the Fishers' exchange puzzle at IPP 20. It was made by Wayne Daniel. In the modified design, two pieces are fused to two others, and the cubic central cavity is occupied by a bisected cube.

	Stewart Coffin and Bill Cutler both independently came up with the design of 12 interlocking notched hexagonal sticks (copied by Tenyo's "Papa" puzzle shown elsewhere). Stewart's version was produced commercially by 3M, who called it "Hectix." I've obtained the red/white/blue, white, and clear versions of Hectix. See U.S. Patent 3721448 - Coffin 1973.
The Hectix design has been widely copied - here is a wooden version produced in Japan as part of the "Woody" line of puzzles: Woody Craft Hexsticks
Joy of Hex - by Two Brass Monkeys in collaboration with Derek Bosch This great product extends the original idea of a burr comprising 12 interlocking notched hexagonal sticks into a family... Borrowing heavily from their website description: They've done an analysis of all solid, twelve-piece burrs, with no solid key piece, and selected and released three designs: MISSIONARY (easiest); BISH, BASH, BOSCH - requiring coordinate motion; and GROUP HEX - incorporates the maximum number of different piece types (8 of 9 possible types of notched hexagonal piece) that has a single unique solution. Included with the three sets are: Five bonus milled brass hex pieces, a "Joy of Hex" manual of 30 hexual positions and solutions written by consultant hexologist Dr Eric Shun, and a hex aid (jig/stand) to help with the most challenging positions. These items turn the three puzzles into a burr set, with 30 published challenges and over 97,000 other possible assemblies. Each hex piece is milled from solid brass and is 6cm / 2.36 inches long. An assembled puzzle weighs about 1.8lbs or 840g. I got the complete set. The entire set weighs in at 8.5lbs. I have accomplished the Missionary position: When I received my example of "Group Hex" it mistakenly included an extra BC rod instead of the required ABC rod. Brass Monkey Steve very kindly and promptly sent me the missing part, and then named an assembly that would utilize the extra BC rod after me - I am honored, probably...
	Some of Stewart's other designs were produced commercially in plastic as part of the Skor-Mor "Geo-Logic" and "Penta-Logics" lines. I obtained Tauri, Cetus, Aries, and Uni in 2-in-1 packs, and a Nova separately. The Penta-Logics included Spirus and another Nova. Luckily, all of the pieces are intact. Each puzzle is composed of a set of six particular identically-shaped pieces (a different piece type for each puzzle), which fit together either in two halves or using coordinate motion. The Tauri is described in Stewart Coffin's book The Puzzling World of Polyhedral Dissections (see fig. 97). The Penta-Logics set allows you to make a "Galaxy 1" (shown, with leftover pieces) and a "Galaxy 2" (not shown).
Aries	Cetus	Nova	Tauri	Spirus	Uni (A real pain to assemble!)
Cetus instructions and six identically shaped pieces.
Tetrahexed - designed by Stewart Coffin, made by Wayne Daniel, exchanged at IPP35 by Stan Isaacs A nice wooden version of Coffin's 1971 Cetus issued by Skor-Mor
Nova			Spirus
Geologic Aries - designed by Stewart Coffin, issued 1972 by Nylon Products Corp. MA
The Geo-Logic line also included an "exploding cube" called "Inner Peace." It has six identical pieces. I obtained one but with no box - I did not know what it was until I found a box shot on the web. The six pieces can be built into a cube or a stellated rhombic dodecahedron. The latter is a very tight fit.

Cross in Ball	Prismastar	Twister 1
UFO	The Hedgehog purchased from Cleverwood	The Trick Box is also a coordinate motion puzzle - darned hard to assemble.
This small 4-piece "Cube Vinco" was a gift from Vaclav at IPP26.	Cubetresor	This is the Button Prison from B & P.
This is Two U. See Vinco's website for a nice chart of various types of "half-cube" puzzles. This puzzle reminds me of Coffin's Pieces of Eight. Purchased from Vaclav at IPP28 in Prague.	This is Vinco's Vidly Half-Cubes. Although technically this isn't an Interlocking puzzle, I show it here since it is another of Vinco's series of half-cube designs. A gift from Vaclav at IPP28 in Prague. Thanks!	Xcruci8 - designed and made by Vaclav Obsivac Exchanged at IPP28 by Laurie Brokenshire Purchased from Laurie at NYPP2011
IPP 31 - octahedron - Vinco
Try-Cycle designed and made by Vaclav Obsivac, exchanged by Laurie Brokenshire

This beautiful spherical puzzle is called the O. S. M. Ball, designed by Jakub Dvorak of the Czech Republic. I purchased this from Bernhard Schweitzer at IPP28 in Prague. Eight pieces. The first and second moves are tricky to discover. Made from beautiful hardwoods.		This is a Muto Cube from Japan. I've seen it on only one other collector's ( Martin Watson's ) site.
These are Oskar's Matchboxes. The first set I got from gemanigames.com. They're not really matchboxes - the "interior" pieces are solid, not hollow boxes. Also, not all interiors fit easily into all containers and the ends have obvious saw marks with overall finish being mediocre. Still, I am happy to have them and the puzzle is fairly challenging. The solution configuration does fit together nicely. I have wanted this puzzle since first reading about it on page 81 of Slocum and Boterman's Puzzles Old and New way back when, and I was glad to find a vendor selling it. Eric Fuller made the second set, from Madrone and Aformosa woods. These are beautiful - the boxes actually have walls and interiors and the fit is great.		Matchbox Play Six designed by Olexandre Kapkan made by Eric Fuller Eric has this to say about this puzzle: "Oskar's Matchboxes is one of my favorite puzzles, and as soon as I saw that Olexandre had expanded on that concept I was eager to make the Matchbox Play Six. With three sets of mirrored pieces, there are several symmetrical solutions and even a couple non- symmetrical solutions. This puzzle is a lot of fun to play with and is a bit easier to solve than the five piece version by Deventer. It displays beautifully and is one you can hand to a trusted guest to experience the feel of a high end puzzle without the frustration of an extraordinarily high level burr. The construction of this puzzle is robust and detailed. Detailed and intricate shoulder joinery on the drawers and sheaths makes it much stronger than the .125" thick wood would indicate. Each puzzle was individually sanded to fit, and the feel is excellent overall."
These are Oskar's Cubes. The large wooden version is from Tom Lensch. The small aluminum version is from B and P. You can see the pieces at Ishino's site.		The Devil's Half Dove-n and the Devil's Other Half Dove-n. Designed by Pavel Curtis. From Puzzlecraft, gifts from LuAnn.
This puzzle is called Six Tabbed Planks. It is made from acrylic. I really like it - the proper configuration can be logically deduced with a little effort, and the assembly is sequential. Unknown designer. Purchased from Pavel Curtis. Pieces shown here.	Six-piece ball (aka Faberge Knot) Made by Lee Krasnow - mechanism is identical to the Six Tabbed Planks from Pavel Curtis.	Caged Spheres (in purpleheart wood) Also purchased from Puzzlecraft.	A 4-piece cube with dovetailed pieces. Designer unknown to me.
This is Arjeu's CT87. This was designed by Oskar van Deventer. Evidently Arjeu never compensated Oskar! Tom Lensch is selling a really nice version.		Myopic Doves by Rick Eason.
Prickly Puzzle, designed, made, and exchanged by Simon Bexfield		The Slump Cube, designed by Ronald Kint-Bruynseels, made from Mahogany and Rosewood by Eric Fuller
This cube was included in an auction lot. I didn't recognize it at the time, but after I received the lot I realized this was a copy of the Frankfort Cube I had wanted after I saw it on Casse-Tete et Solution (scroll down to item #33).
The Tease puzzle cube designed by Sam Cornwell and made from Quilted Sapelle, Wenge, and Carolina White Ash by Eric Fuller. Five pieces, and five moves to get the first piece out.		This is Oskar's Patchwork Box, designed by Oskar van Deventer and made by Tom Lensch. Purchased from Tom at IPP 29 in SF.
A vintage Think puzzle by Chadwick Miller of Massachussetts. Made in Japan. Copyright 1968.
This is Trickstix, by Harris. See U.S. Patent 2473369 - Harris 1947. The similar cage with rotating sticks and a ball inside is a common design.		Adam's Block Puzzle Senior and Panel Puzzle I finally obtained instances of these two in their original packaging.
I have had this small plastic red, white, and blue puzzle cage since I was a kid. Its pieces are more decorated than the Trickstix. This is Adams' Locked Blocks. Adams' Oriental Puzzle seems to be the same design (shown for reference - I don't have that).
The Molecule by Joe Miller. See U.S. Patent 5762336 - Miller 1998. Entered in the IPP 2001 Design Competition.		The Dragon Cube, designed by Doug Engel. Issued by Philos. Purchased in Montreal.
Here are several offered by Bits & Pieces at various times...
Several classic puzzles by Mag-Nif and Reiss that I have had since I was a kid. From Mag-Nif: Four Square, Third Dimension, and the Curious Cross in smokey plastic and blue plastic. Some 1974 Reiss puzzles: Equilibrium, Star, and Reiss' version of Curious Cross, which they call Torment.
Meiji Cheese Curls, and the "Light" version.		Moose Ball - designed and exchanged at IPP35 by Simon Bexfield
Screwy Octahedron a 3D print designed by George Bell		Nuclear Fusion a 3D print designed by George Bell
Stephen Chin of Australia is a skilled woodworker and woodturner. He created a beautiful apple-shaped wooden interlocking / coordinate motion puzzle he calls 1 Pinko Ringo, inspired by Wayne Daniel's 10-piece icosahedron. Stephen's puzzle was among the top 10 vote-getters in the 2010 IPP Design Competition. A similar puzzle by Stephen called the Bomb won the first Rochester Puzzle Picnic Puzzle Competition. Stephen has also created his own version of the icosahedron, known as the "Spinico." Brian Pletcher blogged about it. George Bell did some CAD modeling and after several prototypes to get the angles just right, offers spherical versions of Stephen's design in two sizes at his Shapeways shop. He calls this the Exploding Ball. The puzzle comprises 10 identical very interesting pieces. The dissection using 10 identical pieces was at first thought to be impossible to assemble, but it can be managed. Disassembly can be challenging if you cannot think of a convenient method. I bought the larger version. At IPP35, I was able to purchase a hand-turned wooden version from Stephen: Exploding Apple (aka 1 Pinko Ringo) - made by and purchased from Stephen Chin One of Chinny's signature pieces. He packs it in a sock :-) This was one of the top ten vote getters in the 2010 Nob Yoshigahara Puzzle Design Competition
The Bandai Ultimagear Yu-Gi-Oh Millennium Puzzle I had purchased arrives in its largish box packed like a model - its ABS parts are on a set of sprues. The parts must all be cut free from the sprues, carefully trimmed, and then each puzzle piece can be assembled from its constituents according to included instructions. Each of the puzzle's pieces comprises two or more parts. Fortunately no glue is required - the parts press together, albeit with some firmness needed, and I found all the fits to be satisfyingly precise and snug - the parts are very unlikely to ever be unintentionally (or even intentionally) separated. The resulting puzzle pieces are all robust and none seem prone to break during normal play while respecting the typical mechanical puzzling prohibition against use of undue force. Only 13 pieces left to fit in! No instructions are included for how to assemble the puzzle from its pieces. I attempted assembly guided only by images of the finished puzzle - many times I had made some headway when I realized that I had to unwind several steps to insert a new piece, and furthermore that rotations were required! This is most definitely a sequential interlocking puzzle with rotations along the way, and I am very pleased with its overall quality. It is a bit like a plastic Berrocal - the pieces are not simply polycubes - their shapes are intricate and the placement of each is not necessarily obvious, but with patience can be deduced. Tricky and non-orthogonal movements are needed to sequentially interlock and unlock the pieces during the solve. Cutting free the parts and construction of the pieces took me about three hours, and solving (assembling the puzzle) about a further two hours - there were a couple of moments where three hands would have been helpful during the solve, and I only required one hint.