
 To solve a route-finding puzzle, one must navigate a traveler piece
(sometimes one's whole body - or maybe just a fingertip...) through a pre-established network of routes,
from some starting point to some goal point, perhaps obeying some rules or constraints along the way.
Usually the challenge is to find any route, but sometimes one must find the shortest route among many.
The route-finding class is a subclass of Sequential Movement type puzzles, since where you can go depends
on where you've been - i.e. current state options depend on prior state actions.
The difficulty of route-finding puzzles lies in the confusing complexity of the network, which will usually
present many choices and dead-ends, and in some cases loops.
This is different from a route-building puzzle, where the network is not pre-established
(or at least does not appear to be), but must be constructed from some kind of units (often tiles depicting
route segments), according to some rules (often edge-matching constraints), as play progresses.
To solve a route-finding puzzle, one must navigate a traveler piece
(sometimes one's whole body - or maybe just a fingertip...) through a pre-established network of routes,
from some starting point to some goal point, perhaps obeying some rules or constraints along the way.
Usually the challenge is to find any route, but sometimes one must find the shortest route among many.
The route-finding class is a subclass of Sequential Movement type puzzles, since where you can go depends
on where you've been - i.e. current state options depend on prior state actions.
The difficulty of route-finding puzzles lies in the confusing complexity of the network, which will usually
present many choices and dead-ends, and in some cases loops.
This is different from a route-building puzzle, where the network is not pre-established
(or at least does not appear to be), but must be constructed from some kind of units (often tiles depicting
route segments), according to some rules (often edge-matching constraints), as play progresses.
 Think about a maze
(Wikipedia entry),
and the legend of Theseus and the Minotaur might come to mind.
Confined within a structure on the island of Crete at Knossos, the Minotaur - half-man and half-beast,
and evidently very pissed off,
would claim a human sacrifice each year, until the hero Theseus arrived to slay him.
However, the structure in which the Minotaur was confined is usually called a labyrinth, not a maze.
The distinction lies in the characteristic that a maze contains pathways with intersections - choices which can lead to dead-ends or
run-arounds - while a labyrinth contains essentially only a single path - and is therefore not much of a puzzle, though the
path may be very convoluted on itself.
This being the case, it would be a mystery why Theseus required the help of Ariadne, in the form of a thread spooled from the
entrance, to find his way out.
Let it suffice to say that there remains an absence of universal agreement on the terminology.
Another famous maze appeared in the first computer adventure game,
Advent, and spawned the immortal phrase,
"You are in a maze of twisty little passages, all alike."
This phrase was used as the description of all the locations within the maze, and one would quickly become lost or go in circles.
To map the maze and get through it without relying on sheer luck, the solver had to realize they could drop various items
at different locations in order to distinguish them.
At another point, Advent employed a variation on the original theme -
each location's description was a unique variation on the
phrase "You are in a maze of twisty little passages, all different."
For example, "You are in a twisty maze of little passages, all different."
Once one realizes the descriptions are all actually different, solving the maze becomes easy!
Unfortunately, mazes became over-used in adventure games, often poorly done and coming to be seen as a
hackneyed device for adding time-wasting filler.
Think about a maze
(Wikipedia entry),
and the legend of Theseus and the Minotaur might come to mind.
Confined within a structure on the island of Crete at Knossos, the Minotaur - half-man and half-beast,
and evidently very pissed off,
would claim a human sacrifice each year, until the hero Theseus arrived to slay him.
However, the structure in which the Minotaur was confined is usually called a labyrinth, not a maze.
The distinction lies in the characteristic that a maze contains pathways with intersections - choices which can lead to dead-ends or
run-arounds - while a labyrinth contains essentially only a single path - and is therefore not much of a puzzle, though the
path may be very convoluted on itself.
This being the case, it would be a mystery why Theseus required the help of Ariadne, in the form of a thread spooled from the
entrance, to find his way out.
Let it suffice to say that there remains an absence of universal agreement on the terminology.
Another famous maze appeared in the first computer adventure game,
Advent, and spawned the immortal phrase,
"You are in a maze of twisty little passages, all alike."
This phrase was used as the description of all the locations within the maze, and one would quickly become lost or go in circles.
To map the maze and get through it without relying on sheer luck, the solver had to realize they could drop various items
at different locations in order to distinguish them.
At another point, Advent employed a variation on the original theme -
each location's description was a unique variation on the
phrase "You are in a maze of twisty little passages, all different."
For example, "You are in a twisty maze of little passages, all different."
Once one realizes the descriptions are all actually different, solving the maze becomes easy!
Unfortunately, mazes became over-used in adventure games, often poorly done and coming to be seen as a
hackneyed device for adding time-wasting filler.
 The Cretan labyrinth design has appeared down through the centuries in many decorative and architectural motifs - for example,
on coins and carved in stone - and seems to recur in many cultures.
See examples at
Mirko Elviro's site.
The schematic can be fairly easily constructed -
do an online search for "drawing a labyrinth."
The Cretan labyrinth design has appeared down through the centuries in many decorative and architectural motifs - for example,
on coins and carved in stone - and seems to recur in many cultures.
See examples at
Mirko Elviro's site.
The schematic can be fairly easily constructed -
do an online search for "drawing a labyrinth."

 Interest in mazes and labyrinths continues unabated today.
Adrian Fisher is perhaps today's master maze maker.
Adrian has created many large-scale commissioned mazes, including hedge, corn, and mirror mazes.
Interest in mazes and labyrinths continues unabated today.
Adrian Fisher is perhaps today's master maze maker.
Adrian has created many large-scale commissioned mazes, including hedge, corn, and mirror mazes.
 Aside from large-scale structures meant to be walked through, mazes also appear in many portable mechanical puzzles,
which are our primary concern here.
Starting with the very simple concentric rings in the original Pigs in Clover design,
there have been countless rolling-ball-in-maze puzzles issued.
The Pigs in Clover design is a trivial maze - but the passages and openings are cleverly contrived so that
the challenge of that puzzle is primarily one of dexterity - tilting a ball through one passage will often, frustratingly,
tilt another ball through a different passage in the wrong direction.
I will try to sort out dexterity puzzles and keep them in the Dexterity section,
but the distinction can sometimes be a fine one.
You will also see a blurring of this class with the Tanglement class, since the traveler piece
can be thought of as being tangled in the network, from which it must be freed.
I will also exclude pencil-and-paper printed mazes, though they have become quite complex in their own right,
some even requiring 3-D glasses!
The Hordern-Dalgety classification has several sub-classes of route-finding puzzle:
Aside from large-scale structures meant to be walked through, mazes also appear in many portable mechanical puzzles,
which are our primary concern here.
Starting with the very simple concentric rings in the original Pigs in Clover design,
there have been countless rolling-ball-in-maze puzzles issued.
The Pigs in Clover design is a trivial maze - but the passages and openings are cleverly contrived so that
the challenge of that puzzle is primarily one of dexterity - tilting a ball through one passage will often, frustratingly,
tilt another ball through a different passage in the wrong direction.
I will try to sort out dexterity puzzles and keep them in the Dexterity section,
but the distinction can sometimes be a fine one.
You will also see a blurring of this class with the Tanglement class, since the traveler piece
can be thought of as being tangled in the network, from which it must be freed.
I will also exclude pencil-and-paper printed mazes, though they have become quite complex in their own right,
some even requiring 3-D glasses!
The Hordern-Dalgety classification has several sub-classes of route-finding puzzle:
This section includes basic mazes - they might have multiple levels, wrap around a cube, be "reprogrammable" to make different challenges, pit you against a timer, or release a switch when solved, or even be expressed in the form of a logic puzzle, but the maze is "all there" in front of you and nothing about it changes as you go.

A 2D maze set in a wooden base. |
 Backflip - 2-sided maze - Binary Arts ca. 1990 |

2-sided maze - by WADA Japan (?) or Cole Industries (?) |

Amazing Puzzle Bank - B and P There seem to be many of these hollow maze cube money banks around. |

Bilz Box Another money bank. |

"Jumbo Maze" - a gift from Cleverwood. Thanks! |
 Color Cube Maze - DaMert In this type of maze, the maze panels follow the walls of the cube - the ball can move among the side panels but the interior of the cube is empty. I have seen this called 2D-3D. |

Boston Subway - designed by Oskar van Deventer for the 2006 IPP Exchange made by George Miller (See Boston Subway at Oskar's website.) Boston Subway comprises a "sandwich" of 5 layers of transparent acrylic, through which one navigates an internal metal ball from point A to B and back. Boston Subway requires the solver to use an included magnetic wand to move the ball through the maze. |

Minute Maze - Mag-Nif |

Helix 3 Maze Fury - by Wedgits Three solution goals and paths - shown at wedgits.com. |


Try-It - by Milton Bradley A transparent static cubic maze with a 4x4x4 grid. I found two examples, one in its box. The box says Copyright 1960. This cube featured as a Star Trek prop. Also see Try-It Digitized. |


Miller's Maze - Robert Miller, Creata HK 1983 A transparent static cubic maze with a 5x5x5 grid. |

A-Maze-Ing - by Jajaco, from 1963 A transparent static cubic maze with a 4x4x4 grid. |


Russian Maze - 1988 A transparent static cubic maze with a 6x6x6 grid. |
|



Christopher Sarbaugh 8x8x8 Cube Maze - (aka 8 Cubed or Crystal Maze) 1987 Japan (Tsukuda) A transparent static cubic maze with an 8x8x8 grid. I obtained another copy from Japan, in its original package:
|
||






Monstrous Maze - There are two versions, both made by Tomy in 1982. The red one is called "Straight and Narrow" and the blue one is called "Crazy Curves." 7x10" but with tiny tracks and balls. A rotating circular "corral" at each end allows one to trap the balls. Red solution here. Blue solution here. |
||



Crystal Puzzle - a transparent pyramid I obtained an example from Japan, in its original package:
|
||



Cube Maze - a vintage puzzle by Pantheon - Japan |
||



Maze in a Sphere - Japan I now have the Sphere, Pyramid, and Cube.
|
||

Loncraine Broxton Pyramid Maze 1999 |

Moire Maze - designed by Scott Elliott. Scott writes about his Moire Maze on his blog. |
|


Fire Escape by SmartGames (also sold as "Tower of Logic Inferno") A series of 48 two-sided cards pose route-finding problems. Fit a card into the tower. Ladders, fires, and a victim on each card are visible through the tower. Navigate the fireman from the starting position to the victim, using the ladders and the wrap-around terraces on the tower, and avoiding the fires. The fireman is equipped with one or more colored fire extinguishers which can each be used once to pass through a fire of the corresponding color. (Playing with this last feature admittedly moves this to the Complex category.) |

Ethereal Maze - designed by Steve Winter See Steve's Shapeways shop a gift from Brett - Thanks! |
|



|


|

|
||||||
|
Madmaze, issued in 1970 by Gametime Inc. of NY
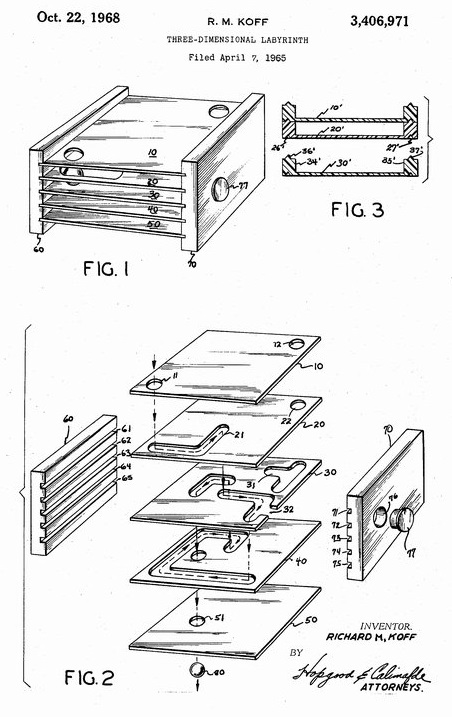
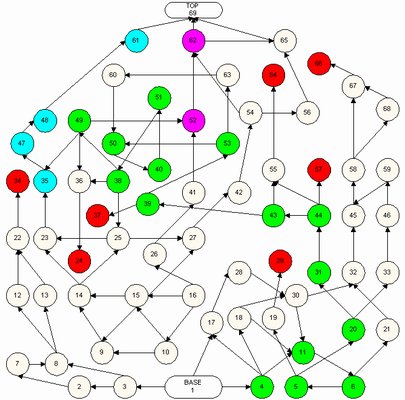
See U.S. patent 3406971 awarded to Richard Koff in 1968 (filed 1965). This is a 5 row x 5 column x 6 layer maze made from acrylic plates containing cutout holes and passageways, and four metal support rods at the corners with spacers and end caps. The top and bottom plates are solid - the enclosed metal marble is not meant to be removed from the maze. (I don't number the top or bottom plate.) Holding the layer with the marks uppermost and numbering them 1-6 from top to bottom, Layer 2 contains diagonally opposed red (starting) and green (goal) marks/resting areas and the objective is to maneuver the marble from the red to the green location. The maze contains dead ends into which the marble will fall unless the maze is oriented properly - you'll have to pick it up and turn it in various ways to guide the ball. I had found a copy without any provenance and hadn't noticed the patent number appearing on the puzzle. Puzzle friend Michel van Ipenburg found a copy that included the box, sent me some photos, and alerted me to the presence of the patent. The pink box and tag with the checked background are Michel's. My original copy is a little beat up and has some cracks, but it still works - I mapped the maze then moved the ball as necessary to solve it. I have since obtained a second copy in an original (green) box - this copy is in much better condition than the first. This reminds me of "Next Floor" by Oskar van Deventer - see it at Oskar's website (scroll down). Below is a map giving the solution for the Madmaze puzzle. Layers 1, 2, and 3 appear left to right in the top row, then layers 4, 5, and 6 are below. The green path gives the solution and the orange paths show dead ends. The starting point is in Layer 1 at the lower left corner and the goal is Layer 1 in the upper right corner. Any location (indicated by the circles) that is colored in adjacent layers allows the ball to move between the layers at that location. Within layers there are no other paths than the colored paths shown.
|
||||||||


|
|
This is the XMATRIX Quadrus puzzle,
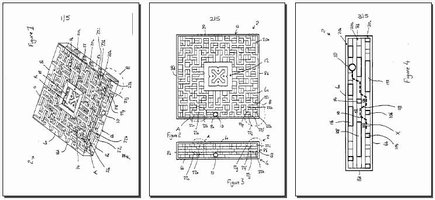
developed in 2009 by artist and designer Jeremy Goode and issued by www.xmatrix.co.uk You can see Goode's European patent GB2472581(A) online. The Quadrus retails for £20 - Jeremy kindly sent me a copy to try. Thanks, Jeremy! Quadrus is a large (140 x 140 x 30mm) and attractive traditional rolling-ball multilevel maze in a gold-tinted transparent acrylic case, nicely packaged in a cardboard slipcase tray that shows off the ambigrammatic XMATRIX logo. Quadrus is also available in a blue tint, and has a smaller cubic sister puzzle called Cubus. In Quadrus, the maze network is defined by three layers of internal latticework structures and interstices - one lattice on each large face, and a third suspended between them, with an empty thickness between pairs of adjacent layers - giving an overall thickness of 5 layers between the "floor" and "ceiling" faces. The walls in a layer are 4mm wide, and the pathways between walls are 8mm wide. Walls and pathways in a layer are arranged on a 34 x 34 virtual grid of 4mm x 4mm squares. The ball occupies a 2x2x2 space within the lattice. The maze contains a central 12x12 square compartment - a white panel with a stylized 'X' cutout separates the compartment into a gold-framed side and a silver-framed side. Each side of the compartment has a single entrance into the maze. To solve Quadrus, one must navigate the ball from the central gold-framed compartment to the central silver-framed compartment on the opposite side, by tilting the puzzle and guiding the ball through the maze. I have found that the occasional ill-planned tilt can send the ball somewhat further than one intends, adding a dexterity dilemma to the already-considerable routefinding challenge. This style of maze is similar to the Boston Subway puzzle designed by Oskar van Deventer for the 2006 IPP Exchange. (See Boston Subway at Oskar's website.) Boston Subway is a much smaller puzzle, but also comprises a "sandwich" of 5 layers of transparent acrylic, through which one navigates an internal metal ball from point A to B and back. Unlike Quadrus, Boston Subway requires the solver to use an included magnetic wand to move the ball through the maze. As interesting as Oskar's Boston Subway puzzle is, I find the Quadrus more convenient to hold and manipulate, and it is far easier to see and keep track of where the ball is. While less portable, it is more engaging to the casual puzzler. For the 2009 IPP, Oskar also designed Next Floor. (See Next Floor at Oskar's website.) Produced from laser-cut MDF, this maze is formed from 5 grooved layers with four interstices. A version of Next Floor is marketed by Bits and Pieces, but unfortunately folks reported that the layers can be loose and the ball can squeeze through unintended paths or even fall out, spoiling the fun. No such issues plague the robust, high-quality Quadrus puzzle. I found an older seven-layer version (in an eBay auction). Unfortunately it included no documentation and I am unaware of its provenance. (NOTE: UPDATE: this has been identified as a MADMAZE from 1970.) 
|
In these mazes, the designers have incorporated various devices to confound the would-be solver. Pieces of the maze might be hidden, or might be movable.
 In this "Maze Ball Game," the segments move and re-configure the maze. |
 The horizontal slices rotate in Raintree's Tower of London, reconfiguring the maze. |
 The Medallion |

Synapse Each leg can rotate on its long axis. The ball must be navigated internally from leg to leg to the exit. |

Missing Marble |
Amazin' Marble Die |



Exit - issued by Reiss in 1974 Place a steel ball into the wooden block, which contains maze passages to be navigated blind. What is odd about the photo on the back? |
||
 Odd Ball |

 Skill-It Milton Bradley 1966 The frying pan contains a maze of half-height walls. A permanently attached but rotating transparent lid has another maze of half-height walls. Maneuver the ball and the lid to get the ball from the center to the handle. (U.S. Quarter in pic for size.) |

Inside Cube Orange |

 No Peekie Ideal 1971 The maze has a lid showing the solution. Close the lid and navigate the ball. Harder than it would seem, as the dead-ends complicate things and you become unsure of just where the ball is. (U.S. Quarter in pic for size.) |
||

Amazers - 1986 Tilton Toys Ltd. |
||
 KO Labyrinth By the Lepato Co. Ltd. Combines a maze with a 3x3x3 twisty sphere. |
 Amaze Here, you can move some of the walls, but only from certain positions and only in certain directions. |

Perpetual Motion, by Bill Darrah A hidden maze. Maneuver the top off. Purchased from Bill at IPP28. Made by George Miller. |

Life's Maze A switched maze, by Kirill Grebnev. |

Octamaze, by Pavel Curtis. Read about Octamaze at Pavel's blog. Pavel has several pages giving progressive hints. |

I found The Black Jack Labyrinth by Constantin at Eureka. |

The No Dexterity maze, designed by Oskar van Deventer and made by Tom Lensch. Set the maze on a table with the single opening in the center of one side face up. Drop in the ball. Now get the ball out back through the same hole. For each move, you may only rotate the maze flat onto a new face without picking it up or shaking it. You must plan your sequence of moves carefully to force the ball to drop from cell to cell using only gravity. |
 22 Card Maze, designed, made, and exchanged by Mike Snyder at IPP32 First, build the maze by arranging the 22 tiles so that all cut-outs are filled by another tile. Then, navigate the maze by always proceeding from a card "on top" to one it is "covering." |
|
 Acrobat designed and made by Diniar Namdarian, exchanged at IPP32 by Goetz Schwandtner |

Paradox Box Designed by Ivan Moskovich, issued by Fat Brain Toy Co. Drop the steel ball bearing into a hole in the corner of the "top" of the cube, then navigate it through the blind maze to an exit hole in the center of the "bottom" face. Various clues on the outside of the box might help - arrows on the clear face panels (up, down, left, right), a 5x5 grid of 10 colors on each face (white, black, purple, red, orange, yellow, light blue, dark blue, light green, dark green), and plus/minus/infinity signs at the grid crossings. What can it all mean? |
|


Vikings Brainstorm - designed by Raf Peeters, issued by Smart Games A 3x3 grid of overlapping circles is populated with a set of nine "water" pieces of two types. These water pieces interlock, rotate, and interfere with each other in interesting ways, and at certain locations there will be boat-shaped gaps. The puzzle includes four Viking boats and each challenge calls for you to move one or more boats from given starting positions to specific goal positions, navigating through the board by figuring out how to exploit the rotating water pieces and gaps. An unusual and very satisfying style of movement! |
||


Simultaneous Maze - designed by William Hu, made by Eric Fuller, from Maple, Jatoba, and Acrylic. |

Turnstile - from Thinkfun - designed by Steve Hayton Set up the turnstiles and men per the challenge card then find the proper sequence of moves to get each man to its home corner. The men can pass through a turnstile only when it is free to rotate. The gray men have no home and simply get in the way. |

Gravity Maze - from Thinkfun, designed by Oli Morris Set up a start and end tower per a challenge card then position additional designated towers to create a path for the marble from start to end. |




Orbis by Brainwright is a sequential-movement route-finding puzzle with 60 graduated challenges. Orbis is a licensed copy of "Marble Monster" by the German company Huch & Friends. It has an unusual mechanic I haven't seen before. After the board is set up per a challenge card, you use the orange "pawn" to move from circle to circle along a hexagonal grid, pushing a single marble on each move, with the goal of eventually being in a position to push the yellow marble into the center. The proper meandering path for the orange pawn is by no means trivial to deduce. This is a great puzzle - if there is a flaw here, it is shared by many similar multi-piece graduated challenges - when you realize you have gone astray and need to start over, resetting the pieces can be a bit tedious. I think this would make a great smartphone app! |
||



The 3 Times and Out Puzzle - a vintage route-finding puzzle |
||


Amazing Cube #1 - ThinkIQ, Mi Toys |


Amazing Cube #2 - ThinkIQ, Mi Toys |


Amazing Cube #3 - ThinkIQ, Mi Toys |


Tvan - designed by Émil Áskerli, made by Johan Heyns from rubberwood (maze plates), pink ivory (end blocks), partridgewood (bars), and wild olive (pins). |
||

Sliding Tetris - Diniar Namdarian Tilt the cage to move the pieces and open up pathways so you can move the ball out. I got the collector's edition with extra pieces (not shown). |

The Case of the Priceless Coin - Professor Puzzle The Priceless Coin is a hidden maze - navigate the coin disk in and out. |

Inside 3 Legend - The Castle - one in a series of 2-layer hand-held rolling-ball mazes (the bottom layer is hidden) having different themes - I received three including The Castle, The Ninja, and The Crypts. They were available via a Kickstarter-like campaign at the French site Ulele. |

Bonbon - Jean Claude Constantin. Thanks, Chelsea! |


Maze Cube - by Yavuz Demirhan |
|



Modular Maze - Collier Products A vintage maze construction kit. |
||
|
Recent Toys has issued a series of puzzles by Constantin, and puzzle-friend Jaap G. very kindly sent me a set. Thanks!
Included are: Tough Measures (a folding puzzle, not a maze), Hidden Corridor, Flower Maze, Waiter's Tray, and Double Trouble.
|
||

Screw Loose One of the "Lost Puzzles of My Childhood." Issued in 1970 by Lakeside Industries, a division of Leisure Dynamics Inc. The packaging says "patent pending" but I could find no online record of the application. |

Dool-O-Rinth set This is a recent series of puzzles called "Dool 'O' Rinth" (aka Crazy Maze) made by CorToys. There are 6 puzzles in the series - in order from easiest to hardest: yellow, orange, green, blue, red, and black. (According to the vendor from whom I purchased it, the red sleeve on an orange spool is a special edition. Since the sleeve contains the maze, this is a red.) Recently re-branded as "Groove Tube." |


Two sleeve-on-cylinder type mazes (Blindlabyrint) designed in 1983 by Lauri Kaira. Only 2000 copies of each were made; most were sold back in 1984. 1A is a single-track labyrinth; 1C is a branching maze. Purchased from Finnish company Oy Sloyd Ab. |

This is Mental Block Puzzle #6 Double Semi-Maze, by R. D. Rose. It is crafted from aluminum, and consists of an outer sleeve with various paths (some not visible) and two half-cylinders riding inside. One of the half-cylinders has a mark on its edge corresponding to a similar mark on the sleeve's edge. The objective is to move the inner cylinder's mark through a full 360 degree circuit. Neither inner piece is meant to come out of the sleeve. |


Tube Maze a sleeve-on-cylinder maze, 3D printed on his Makerbot by Jon Taylor. You might be able to find one for sale via his eBay account 19snowden89. |
|




3D Printed Nested Cylinder Maze Set - from an online auction seller |
|

Cylinder Maze - by Bad Astronaut. |
|

Lockpick Puzzle - by Devin Montes. Kind of the inverse of a sleeve-on-cylinder - in this case the lock body contains the maze and the key must be navigated to extraction. |
|






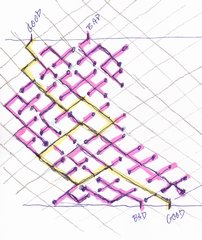
The Roto-Maze issued by Little Harbor Corp. of Lewiston, Maine. Mine is labeled as a "Chevron" pattern, of Intermediate difficulty. The last image is a copy of my hand-drawn solution. Jerry Slocum's collection contains a copy with a rectilinear pattern, and a copy with a curly pattern. |
|

(I don't have this.) At our September 2014 LSC get-together, I had the opportunity to play with (solve and restore) R. Hess' instance of an original vintage Cooksey Maze puzzle issued by Pentangle. The peg seen at the bottom can be pushed in and toggles back and forth with a satisfying "snick" between the position in the photo, and the diametrically opposite position across the cylinder, thus engaging different slots within the maze sleeve. One must navigate the sleeve off the bottom of the cylinder by a series of rotations, downward and upward slides, and pin toggles. Way cool! Oskar van Deventer has designed a simplified version, available at Oskar's Shapeways shop. Oskar also offers several varieties of the Cooksey Tribute. |
|



At auction I won a special edition Blue (BU00006SE), and a Bronze. I've also acquired an Extreme Silver (V2) - as of this writing, very few people in the world (less than 100) have solved one! Revomaze has issued several products - the main series of puzzles are called the Extreme V1 series. They include the Blue, Green, Bronze, Silver, and Gold (in increasing level of difficulty) and the Titanium which was only offered in a collector's edition set. Shown below for reference (I don't have this).  The Extreme V1 series is made from aluminum and nickel-plated brass.
The Extreme V1 series is made from aluminum and nickel-plated brass.
From the manufacturer, here is a video of the series. Here are some notes on and links to reviews of the series members:
|
Revomaze has also issued an Extreme V2 series that have smooth bodies -
including the blue, green, and bronze.
The mazes are identical to their V1 counterparts.
There have also been several Limited Edition (LE) puzzles issued:
|

Clear Revomaze Sleeve - purchased from, and designed and made by Neil Hutchison. Neil discusses the genesis of the clear sleeve in his 30 Dec. 2012 blog post, with a follow-up on 5 Feb. 2013. Allard reviewed his on his own blog. The clear sleeve has also been discussed on the Revomaze forum. |
|
Here are some Shuttle maze puzzles, where the maze is navigated by some element other than a rolling ball.



"16 to 1" - a vintage original shown on the left, a repro from Bits and Pieces, and Hanayama's version called Laby U.S. Patent 598855 - Carter 1898 This is a 2-sided maze, and the shuttle requires you to solve both sides simultaneously. The "16 to 1" name comes from a political issue in the United States of the 19th century concerning monetary policy and the use of silver and gold. Wikipedia's article Free Silver has more information, as does this article at the Vassar website. |
|




Vermont Castings Maze Like the 16-to-1 puzzle, this is a 2-sided maze. It was issued circa 1981 by Vermont Castings, of Randolph Vermont, as a premium accompanying stove purchases. It seems like the objective is to move the shuttle on and then visit the four areas marked I, II, III, and IV (in the first photo). |
|

Coin Maze - a 3D-printed double-sided maze designed by Oskar van Deventer, produced by pghpuzzles. If you think about it, the enclosure acts as the shuttle here. Also, as in the Cooksey Maze, the "coin" must shift from one "prong" of the shuttle/enclosure to the other as you progress. |
|


Oskar's Cube In plastic and in metal Here, the shuttle forces you to solve three mazes simultaneously! |
 Culax Culax is an enhancement to Oskar's Cube - now the shuttle can be rotated within the network. |
 George Miller's Moby Maze is a maze on the surface of a Moebius Strip - it's got only one side, but it behaves like a 2-sided maze! |


Hanayama Cast Moebius - designed by Oskar van Deventer |

 Brain-Chek - two-state faces, and three-state traffic lights. Here, the shuttle interacts with the network as it moves, and changes the state of the nodes. You must find a route such that all the nodes achieve the desired state. |

Cubane designed by Masumi Ohno, purchased from and made by Eric Fuller from Shedua and Bloodwood. 15 moves to get the shuttle from start to free. |

Reversible Maze Large - designed by Masumi Ohno, from CubicDissection |
|

Bookworm - Doug Engel |
Fishyhookery - Doug Engel |


Smart Egg - designed by Andras Zagyvai
There is also a set of four "Smart Egg Dragon" 2-layer puzzles in increasing difficulty levels:
|
|
 Color Cubes |
 Cmetricks Cubicle |

Hedgehog Escape, designed by Oskar van Deventer and Wei-Hwa Huang, and issued from Popular Playthings. |

Creeping Block - exchange from Dirk Weber Thanks, Dirk! |

Say Cheese - Popular Playthings A rolling-block route-finding puzzle, designed by Eric Harshbarger. |
 Creeping Block 3D, designed by Dries de Clercq, made and exchanged by Dirk Weber at IPP32 |


Tut's Tablet - a rolling cube maze Invented by Sjaak Griffioen Produced 2012 Popular Playthings |

CoCoCross - issued by Brainwright A set of graduated rolling-block challenges with two different blocks and an ingenious and convenient compact case. |

 River Crossing (and River Crossing 2) - Thinkfun
"River Crossing" is a commercial version of a type of puzzle known as "plank" puzzles.
Plank puzzles were invented by UK maze enthusiast Andrea Gilbert.
Visit Andrea's website Clickmazes.com.
You can visit the
River Crossing Home Page at Puzzles.com.
Here is a link to play plank puzzles on-line at Clickmazes.com.
River Crossing (and River Crossing 2) - Thinkfun
"River Crossing" is a commercial version of a type of puzzle known as "plank" puzzles.
Plank puzzles were invented by UK maze enthusiast Andrea Gilbert.
Visit Andrea's website Clickmazes.com.
You can visit the
River Crossing Home Page at Puzzles.com.
Here is a link to play plank puzzles on-line at Clickmazes.com.


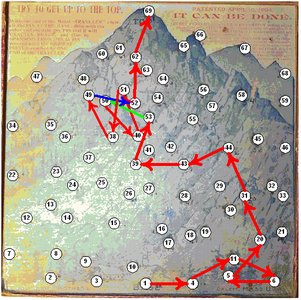
This is a vintage puzzle called "Pike's Peak or Bust." It was patented by Judson M. Fuller in 1894 (518061) and made by Parker Brothers circa 1895. Move the metal traveler from peg to peg from the base to the top of Pike's Peak. Featured in Slocum and Botermans' "Puzzles Old & New" on page 136.
Here is my solution:

 "Yankee Puzzle
"Yankee Puzzle
 Sunflower |


Bronco designed by Oskar van Deventer. Move the Bronco out of the starting gate. I have the early version at left. Recent Toys offers a mass-produced version shown at right (which I do not have). |
 Another Oscar van Deventer design made by George Miller - Free Willy. |
 The Rotten Apple Yet another Oscar van Deventer design made by George Miller. |
 Oskar's Sunflower design was picked up by Hanayama, who created an entry called O'Gear
in their wonderful "Cast" puzzle series.
This is my solution to the Hanayama Cast O'Gear puzzle...
The puzzle consists of two pieces - a hollow cube and a "key."
The key piece has five tabs, and on one side there appear "dots" imprinted on the tabs.
There is one tab having a hole through it.
Hold the key so that the tab with the hole is on top and the side with the dots is facing you.
Number
the tabs starting with assigning 1 to the tab clockwise of the tab with the hole.
This tab number 1 has a notch in one edge.
Proceed clockwise, ending by assigning 5 to the tab with the hole.
Tab 4 will also have a notch in it.
The cube has six faces and a crossed hole in each face.
One hole contains an extension which allows tab 1 to be freely inserted into and withdrawn from the cube.
This is the exit hole.
Once a tab is inserted into the cube, the key can be "rolled" in various directions around the cube, transitioning
from face to face without being released via the clever geometry of the key and holes.
On each face, the key can also be twisted to re-orient the direction in which the dots side of the key is facing.
The cube face opposing the exit face contains 2 small holes at diagonally opposing corners,
which permit the key to "perch" on this face. This is the start hole.
Another face contains a small triangular symbol.
Hold the cube so that the face with the exit hole is upwards and the face with the triangular symbol is facing you.
Label the face which is upwards Up (U) and the face which is downwards Down (D).
Label the face towards you South (S), the face away from you North (N), the face to the right East (E),
and the face to the left West (W).
Using these conventions it is now possible to uniquely label every possible state of the puzzle using three characters:
first, the letter of the face in which the key is currently embedded.
Second, the number of the tab embedded in the cube.
Third, the direction in which the dots side of the key is facing.
The number of total possible states is 120: 6 cube faces X 5 tabs X 4 key facings possible for each cube face.
These 120 states can be depicted as nodes in a graph.
The exit node is U1N. The "perching" state can be reached from either D5S or D5E.
Each of these 120 nodes can be connected by at least one and at most three edges to other nodes:
a single edge representing
the act of twisting the key while remaining on the same face and tab and thus changing the direction in which the
key is facing;
an edge representing rolling the key clockwise
(relative to looking at its dot face); and an edge representing rolling the key counterclockwise.
Not every face of the cube permits all possible actions - you will note that some of the cube's edges are rounded
while others are sharp.
The sharp edges prohibit the key from rolling across them.
Oskar's Sunflower design was picked up by Hanayama, who created an entry called O'Gear
in their wonderful "Cast" puzzle series.
This is my solution to the Hanayama Cast O'Gear puzzle...
The puzzle consists of two pieces - a hollow cube and a "key."
The key piece has five tabs, and on one side there appear "dots" imprinted on the tabs.
There is one tab having a hole through it.
Hold the key so that the tab with the hole is on top and the side with the dots is facing you.
Number
the tabs starting with assigning 1 to the tab clockwise of the tab with the hole.
This tab number 1 has a notch in one edge.
Proceed clockwise, ending by assigning 5 to the tab with the hole.
Tab 4 will also have a notch in it.
The cube has six faces and a crossed hole in each face.
One hole contains an extension which allows tab 1 to be freely inserted into and withdrawn from the cube.
This is the exit hole.
Once a tab is inserted into the cube, the key can be "rolled" in various directions around the cube, transitioning
from face to face without being released via the clever geometry of the key and holes.
On each face, the key can also be twisted to re-orient the direction in which the dots side of the key is facing.
The cube face opposing the exit face contains 2 small holes at diagonally opposing corners,
which permit the key to "perch" on this face. This is the start hole.
Another face contains a small triangular symbol.
Hold the cube so that the face with the exit hole is upwards and the face with the triangular symbol is facing you.
Label the face which is upwards Up (U) and the face which is downwards Down (D).
Label the face towards you South (S), the face away from you North (N), the face to the right East (E),
and the face to the left West (W).
Using these conventions it is now possible to uniquely label every possible state of the puzzle using three characters:
first, the letter of the face in which the key is currently embedded.
Second, the number of the tab embedded in the cube.
Third, the direction in which the dots side of the key is facing.
The number of total possible states is 120: 6 cube faces X 5 tabs X 4 key facings possible for each cube face.
These 120 states can be depicted as nodes in a graph.
The exit node is U1N. The "perching" state can be reached from either D5S or D5E.
Each of these 120 nodes can be connected by at least one and at most three edges to other nodes:
a single edge representing
the act of twisting the key while remaining on the same face and tab and thus changing the direction in which the
key is facing;
an edge representing rolling the key clockwise
(relative to looking at its dot face); and an edge representing rolling the key counterclockwise.
Not every face of the cube permits all possible actions - you will note that some of the cube's edges are rounded
while others are sharp.
The sharp edges prohibit the key from rolling across them.
Here is a path from Start to Exit:
D5E - D5S - E1S - E1U - S5U - W4U - N3U - N3E - D2E - D2S - E3S - E3U - S2U - W1U - N5U - N5E - U1E - U1N
 This is my nicest route-finding puzzle - it is called The Wanderer. Tom Lensch made it. |
 Hanayama picked up the Wanderer, too, and calls it Cuby. |

|

|

|
|
 Oskar's Disks |
||
 Free the Key |
 Locomotion |
 Big Wheel |

19th Hole - Pentangle |

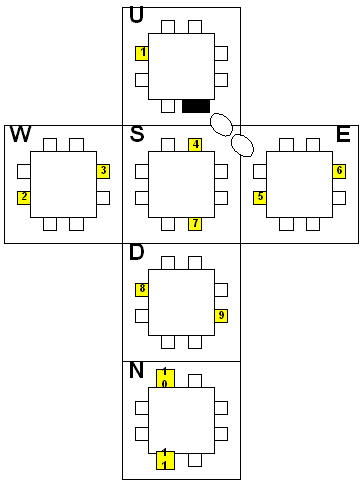 Here is my analysis of Hanayama's Cuby puzzle.
Don't read too far if you want to try this great puzzle yourself!
The Cuby is another wonderful design from the diabolical mind of Oskar van Deventer.
This puzzle consists of a traveler (originally known as the Wanderer) shaped like a quarter of a watermelon, and
a hollow cubic cage.
Here is my analysis of Hanayama's Cuby puzzle.
Don't read too far if you want to try this great puzzle yourself!
The Cuby is another wonderful design from the diabolical mind of Oskar van Deventer.
This puzzle consists of a traveler (originally known as the Wanderer) shaped like a quarter of a watermelon, and
a hollow cubic cage.
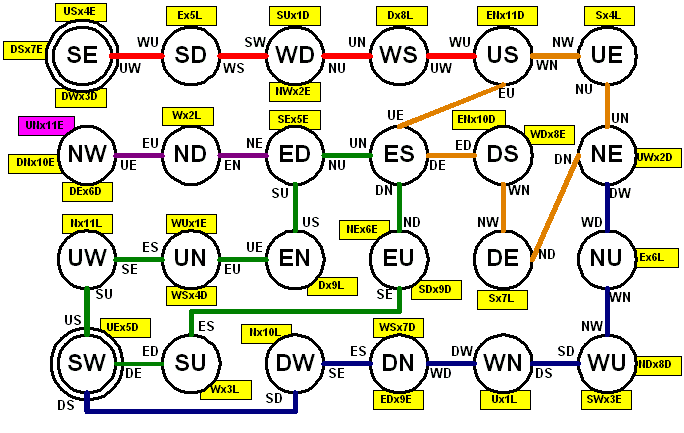
A move consists of two parts - first, retract the traveler fully into one of the two faces through which an end is poking, then rotate the other end into one of two perpendicular faces. So from each state, there are 2x2=4 possible moves - however, because of the missing notches, some will be prohibited since the peg will be blocked in some way. In my notation, a move is also labeled using two letters - first, the face into which you retract the traveler, then the face toward which you move the opposite end. The moves (and their inverses) are given on the arcs of the graph.
The graph has five "zones" - the red portion is kind of a "railroad" from state US to the solution. There is one dead end, shown in purple. There are three loops, in orange, green, and blue. Here is my eight-step solution sequence - states are shown in parens and moves between them:


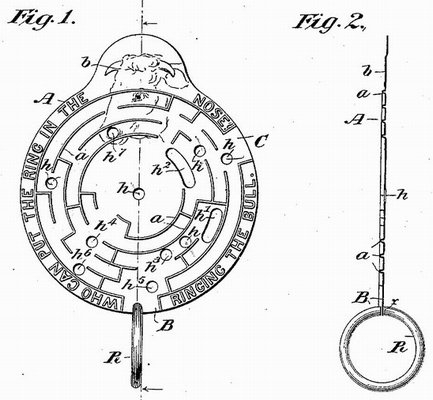 I finally found an example of the vintage Maze Puzzle, patented in 1892 by Joel W. Thorne
(483820)
(483820 on Google Patents)
I finally found an example of the vintage Maze Puzzle, patented in 1892 by Joel W. Thorne
(483820)
(483820 on Google Patents)
This is a ring-in-plate type maze - mine is missing the ring. Interestingly, the patent specifies an extra "decoy" hole, and a bull motif not used by the actual puzzle. The gap in the ring is supposed to be only just wide enough to fit the plate, not the raised maze walls. Also, note the elongated holes, which will allow the ring position to be adjusted for certain moves. Both those features are unusual for a ring-in-plate maze. |



Eureka Puzzle - A nice brass ring-in-plate maze puzzle, with its ring. Marked with its name and "PAT APD. FOR." 2 1/16" in diameter. 18 step solution. The disk is thick enough to be nicely rigid. The ring is relatively thick and its gap is precise - the puzzle operates smoothly, unlike many of its imitators. I had no idea what this was, other than thinking it another run-of-the-mill ring-in-plate puzzle, until I did some research. Now I am very happy to have found this, and it was a bargain at only $7.50 delivered!
The Eureka Puzzle
appears in Jerry Slocum's collection
and on page 108 of Slocum and Botermans' 1994
But note that Appleton says the invention is "a communication to me by Amos B. Paulson of Philadelphia." I was able to
find a Paulson patent - Canadian patent CA49134 issued on June 6 1895
I was unable to find a relevant Paulson patent in the US database.
For my photos and discussion I arbitrarily oriented the puzzle so the logo on my copy
These help in recognizing that the design is repeated in several other similar
There is a vintage Cracker Jack giveaway called the Spider Web Puzzle
that also has the same pattern of holes and the same solution. I was able to find a copy in its original envelope.
The Cracker Jack Spider Web is accurately made - the normal solution works and no illegal moves are permitted.
Regarding the Spider Web in the Sherm's Super Puzzles set,
the solution diagram is misleading
The Gilbert Spider Web appears in
an instruction booklet copyrighted in 1920 (PDF - scroll to page 10).
|


The Spider Puzzle made in Occupied Japan |








(The above appear in the Tanglements section, too. The puzzles shown below do not.)





 At left is Kohner's Toothache puzzle, from 1971.
Maneuver the C ring from the upper left to the lower right. It does not exit the board.
This was a member of a series of Kohner puzzles, which also included Heartache (1971) (see my section on Sliding Piece Puzzles),
and Belly-Ache (which I do not have).
You may also remember Headache, which was a Pop-O-Matic game, not a puzzle.
At left is Kohner's Toothache puzzle, from 1971.
Maneuver the C ring from the upper left to the lower right. It does not exit the board.
This was a member of a series of Kohner puzzles, which also included Heartache (1971) (see my section on Sliding Piece Puzzles),
and Belly-Ache (which I do not have).
You may also remember Headache, which was a Pop-O-Matic game, not a puzzle.



Board 231 - designed and made by Czech craftsman Vaclav Skopek
See his
Etsy store SHOKCZ
A very steampunk instance of a ring-in-plate maze





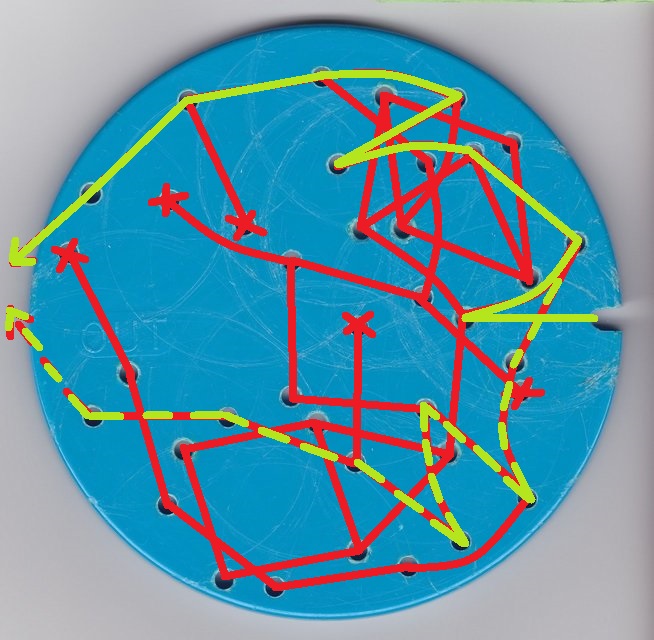
In this type of maze, multiple plates and/or travelers must be moved in coordination.

Saunders' puzzle aka the National Puzzle U.S. patent 766118 - Samuel L. Saunders - 1904 The traveler piece comprises two small brass buttons connected by a short axle - the axle rides in the channels cut in the circular plates. The two plates are connected in the center by a hollow rivet and can be rotated with respect to each other. Both plates are identical - the one in back is flipped. The objective is to navigate the traveler from the central hole towards the outside where it comes free, then back in, via the channels formed when the two plates are moved into various alignments. |
 Mysterians - Designed by Oskar van Deventer and presented by Nick Baxter at IPP23 in Chicago. Made by and purchased from George Miller Named after the '60s rock group the ???Mysterians, who had one hit 96 Tears. The three plates each contain one question-mark-shaped channel. The acrylic barbell traveler comes free after 124 correct moves. |

Hanayama's L'Oeuf Designed by Oskar van Deventer |

Holey Plates and Holey Plates II Markus Goetz See U.S. patent 932147 - Levine 1909. |



The 4D puzzle and the Maze Medal - both designed by Oskar van Deventer The former was made by and purchased from George Miller, whereas the latter is a mass-produced version of the same essential puzzle. Comparison photo at right. |
||
|
This is an original vintage Cross and Crown puzzle.
U.S. patent 1071874 - Louis S. Burbank - 1913

|
|||
(2013 version shown compared with smaller metal original) Updated version arranged by Michel van Ipenburg based on my original example and made by Robrecht Louage exchanged by Dr. Goetz Schwandtner The disk and cross material is "trespa." |
|||

Cross and Crown 7 organized by Michel van Ipenburg and made by Robrecht Louage. A higher-level version of the original 1913 Cross and Crown - C & C 7 requires 4802 moves! |


Ling Meiro / Panel & Ling An interesting ring-in-plate maze from Japan. Three maze cards - blue-green (level 1), yellow (level 2), and pink (level 3), each fit into a shuttle that contains a sliding 4x4-hole frame and the ring. You must navigate the ring, within the frame, from each card's start position to its goal position. |
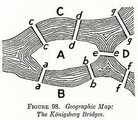 In graph theory, an
Eulerian Path
is a tour which visits each edge exactly once.
The tour is allowed to cross itself - i.e. vertices may be visited more than once.
(If you think about it, you'll note that no vertex can be omitted.)
An Eulerian Circuit is a tour that starts and ends at the same vertex - it's a closed path.
This terminology follows the famous mathematician
Leonard Euler
who investigated the
Seven Bridges of Koenigsberg
problem in 1736.
A unicursal puzzle calls for you to find an Eulerian Circuit (sometimes just an Eulerian Path) of a graph.
Sometimes they're called single-stroke figures.
One must draw the required path from start to finish without taking
one's pencil from the paper and without retracing any edge -
though crossing an already-drawn segment is usually allowed
(although technically you're not supposed to cross any segment more than once).
Here is a pertinent key result from graph theory: a graph will have an
Eulerian Circuit only if it has no odd nodes, and will
have an Eulerian Path only if it has exactly two odd nodes (in which case your path must begin at one of the odd nodes and end at the other).
If you can represent the graph correctly and determine the degree of each node, you can easily tell if you can solve
a unicursal puzzle.
Unicursal problems are discussed in Ball and Coxeter's Mathematical Recreations and Essays (11th Ed. 6th printing 1973)
in Chapter IX starting on page 242.
You can see some unicursal drawing problems at
The Unicursal Marathon.
There are also several unicursal puzzles at
mathpuzzle.ca.
Hoffmann gives some Single-Stroke Figure problems in Chapter X, No. IX.
In graph theory, an
Eulerian Path
is a tour which visits each edge exactly once.
The tour is allowed to cross itself - i.e. vertices may be visited more than once.
(If you think about it, you'll note that no vertex can be omitted.)
An Eulerian Circuit is a tour that starts and ends at the same vertex - it's a closed path.
This terminology follows the famous mathematician
Leonard Euler
who investigated the
Seven Bridges of Koenigsberg
problem in 1736.
A unicursal puzzle calls for you to find an Eulerian Circuit (sometimes just an Eulerian Path) of a graph.
Sometimes they're called single-stroke figures.
One must draw the required path from start to finish without taking
one's pencil from the paper and without retracing any edge -
though crossing an already-drawn segment is usually allowed
(although technically you're not supposed to cross any segment more than once).
Here is a pertinent key result from graph theory: a graph will have an
Eulerian Circuit only if it has no odd nodes, and will
have an Eulerian Path only if it has exactly two odd nodes (in which case your path must begin at one of the odd nodes and end at the other).
If you can represent the graph correctly and determine the degree of each node, you can easily tell if you can solve
a unicursal puzzle.
Unicursal problems are discussed in Ball and Coxeter's Mathematical Recreations and Essays (11th Ed. 6th printing 1973)
in Chapter IX starting on page 242.
You can see some unicursal drawing problems at
The Unicursal Marathon.
There are also several unicursal puzzles at
mathpuzzle.ca.
Hoffmann gives some Single-Stroke Figure problems in Chapter X, No. IX.
 A Hamiltonian Path
is kind of the complement of an Eulerian Path - it visits every vertex exactly once,
but may repeat and omit edges.
A Hamiltonian Circuit starts and ends at the same vertex (which, therefore, you're allowed to visit twice).
A Hamiltonian Path
is kind of the complement of an Eulerian Path - it visits every vertex exactly once,
but may repeat and omit edges.
A Hamiltonian Circuit starts and ends at the same vertex (which, therefore, you're allowed to visit twice).
 The
Knight's Tour
puzzle is also a type of unicursal route-finding puzzle, requiring the discovery of a Hamiltonian Path
around the 64 squares of
a chessboard, following the edges that connect them defined by legal knight's moves.
Both closed circuits as well as open paths are possible.
Dan Thomasson gives some example puzzles on his site.
The
Knight's Tour
puzzle is also a type of unicursal route-finding puzzle, requiring the discovery of a Hamiltonian Path
around the 64 squares of
a chessboard, following the edges that connect them defined by legal knight's moves.
Both closed circuits as well as open paths are possible.
Dan Thomasson gives some example puzzles on his site.



 Here is an example of a unicursal puzzle.
It's called Chain 16 and was issued by the "Are Jay Game Co., Inc." of Cleveland Ohio.
David Singmaster calls this pattern the brick pattern and cites several references to it in the puzzle literature.
One challenge associated with the brick pattern is to draw it in only 3 strokes.
This is impossible, but drawing it in 4 strokes is possible.
Another challenge is to draw a path crossing every wall once - this is the challenge posed by the Chain 16 puzzle.
Chain 16 is simply a wooden block printed with a figure of the bricks pattern, and a long thin brass chain.
The "Object of the Puzzle" is as follows:
"There are 16 'walls' with an opening in each. Using the chain, can you lay out one continuous line going
through each opening? You are not allowed to go through the same opening more than once or cross over the chain."
Trick solutions entail having the path go through a vertex, or within a wall.
Another trick, when the puzzle is printed on paper, entails folding the paper.
I don't think they're valid.
The brick pattern puzzle is mentioned in Gardner's First Scientific American Book of Mathematical Puzzles and Games, in
Chapter 12.
It is also discussed in Dudeney's Amusements in Mathematics, as problem #239,
where the object is to draw the pattern in three strokes.
Dudeney includes it again in 536 Puzzles & Curious Problems, as #414 "Crossing the Lines,"
where the challenge of drawing the path crossing each wall once only is discussed.
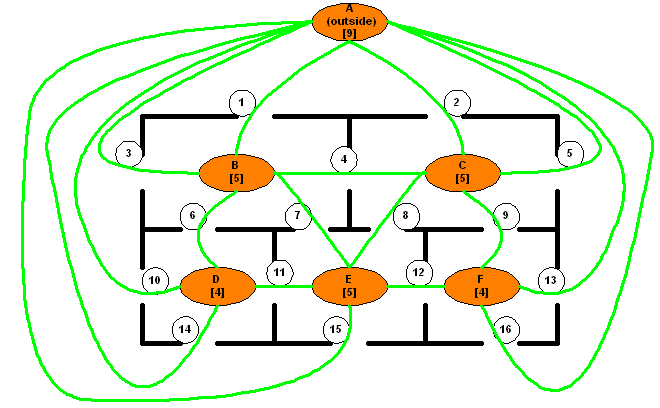
I've drawn a graph overlaying the puzzle and defined six nodes A through F,
with sixteen paths labeled 1 through 16 by the small circles, corresponding to the
openings. I've also shown the degree of each node in brackets.
Here is an example of a unicursal puzzle.
It's called Chain 16 and was issued by the "Are Jay Game Co., Inc." of Cleveland Ohio.
David Singmaster calls this pattern the brick pattern and cites several references to it in the puzzle literature.
One challenge associated with the brick pattern is to draw it in only 3 strokes.
This is impossible, but drawing it in 4 strokes is possible.
Another challenge is to draw a path crossing every wall once - this is the challenge posed by the Chain 16 puzzle.
Chain 16 is simply a wooden block printed with a figure of the bricks pattern, and a long thin brass chain.
The "Object of the Puzzle" is as follows:
"There are 16 'walls' with an opening in each. Using the chain, can you lay out one continuous line going
through each opening? You are not allowed to go through the same opening more than once or cross over the chain."
Trick solutions entail having the path go through a vertex, or within a wall.
Another trick, when the puzzle is printed on paper, entails folding the paper.
I don't think they're valid.
The brick pattern puzzle is mentioned in Gardner's First Scientific American Book of Mathematical Puzzles and Games, in
Chapter 12.
It is also discussed in Dudeney's Amusements in Mathematics, as problem #239,
where the object is to draw the pattern in three strokes.
Dudeney includes it again in 536 Puzzles & Curious Problems, as #414 "Crossing the Lines,"
where the challenge of drawing the path crossing each wall once only is discussed.
I've drawn a graph overlaying the puzzle and defined six nodes A through F,
with sixteen paths labeled 1 through 16 by the small circles, corresponding to the
openings. I've also shown the degree of each node in brackets.

|

Rectangle String Route, designed by Tod Muroi, made by Here to There Puzzles, exchanged by Saul Bobroff at IPP32 Given a large tile with 5 horizontal and 5 vertical evenly-spaced grooves cut into each face and wrapping around the edges, route the single string through all the channels without crossing itself. The route must be a mirror image on the opposite side of the grid. |

Thread the Maze Golf Tangle Invented by Shane Murphy The history of the Thread the Maze puzzle is online at toy-and-game-inventor-success.com. |

Thread the Maze: The Riddle of the Sphinx - by Blue Opal Copyright 1999 Dugald Keith; invented by Shane Murphy and Dugald Keith Thread the cord through every hole just once from start to finish but never leave the tunnels on either side of the card. Check out a nice writeup on Thread the Maze prototyping. |